Lift (force)

For other uses, see Lift.

Boeing 747-8F landing

A fluid flowing past the surface of a body exerts a surface force on it. Lift is the component of this force that is perpendicular to the oncoming flow direction.^[1] It contrasts with the drag force, which is the component of the surface force parallel to the flow direction. If the fluid is air, the force is called an aerodynamic force.

Overview

Forces on an airfoil.

Lift is commonly associated with the wing of a fixed-wing aircraft, although lift is also generated by propellers; kites; helicopter rotors; rudders, sails and keels on sailboats; hydrofoils; wings on auto racing cars; wind turbines and other streamlined objects. While the common meaning of the word "lift" assumes that lift opposes gravity, lift in its technical sense can be in any direction since it is defined with respect to the direction of flow rather than to the direction of gravity. When an aircraft is flying straight and level (cruise) most of the lift opposes gravity.^[2] However, when an aircraft is climbing, descending, or banking in a turn, for example, the lift is tilted with respect to the vertical.^[3] Lift may also be entirely downwards in some aerobatic manoeuvres, or on the wing on a racing car. In this last case, the term downforce is often used. Lift may also be horizontal, for instance on a sail on a sailboat.

An airfoil is a streamlined shape that is capable of generating significantly more lift than drag.^[4] Non-streamlined objects such as bluff bodies and plates (not parallel to the flow) may also generate lift when moving relative to the fluid.

Description of lift on an airfoil

There are several ways to explain how an airfoil generates lift. Some are more complicated or more mathematically rigorous than others; some have been shown to be incorrect.^[5][6][7] For example, there are explanations based directly on Newton’s laws of motion and explanations based on Bernoulli’s principle. Both principles can be used to explain lift, but each appeals to a different audience.^[8] This article will start with the simplest explanation; more complicated and alternative explanations will follow.

Newton's laws: lift and the deflection of the flow

Deflection

Airstreams around an airfoil in a wind tunnel. Note the curved streamlines above and below the foil, and the overall downward deflection of the air.

One way to understand the generation of lift is to observe that the air is deflected as it passes the airfoil. Since the foil must exert a force on the air to change its direction, the air must exert a force of equal magnitude but opposite direction on the foil. In the case of an airplane wing, the wing exerts a downward force on the air and the air exerts an upward force on the wing.^{[10][12][13][14][15][16]}

This explanation relies on the second and third of Newton's laws of motion: The net force on an object is equal to its rate of momentum change, and: To every action there is an equal and opposite reaction.^[17]

Another way to describe deflection is to say that the air "turns" as it passes the airfoil and follows a path that is curved. When airflow changes direction, a force is generated.^[18]

Pressure differences

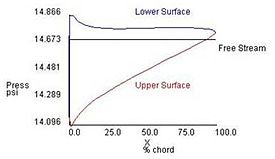
Lift may also be described in terms of air pressure: pressure is the normal force per unit area. Wherever there is net force there is also a pressure difference, thus deflection/flow turning indicates the presence of a net force and a pressure difference. This pressure difference implies the average pressure on the upper surface of the wing is lower than the average pressure on the underside.^[19][20][21]

Flow on both sides of the wing

In the picture above, observe that the air is turned both above and below the wing so both the upper and lower surface contribute to the flow turning and therefore the lift.

Variation of the pressure around an airfoil as obtained by a solution of the Euler equations.

In fact, for typical airfoils at subsonic speeds the top surface contributes more flow turning than the bottom surface, and the pressure deviation along the top is significantly larger than along the bottom. A common explanation describes lift as merely the result of the air molecules bouncing off the lower surface of the wing, but since this ignores the airflow around the top of the wing it usually leads to incorrect results. However, at hypersonic speeds, this model becomes applicable.^[22][23][24]

Criticisms of deflection/turning

• While the theory correctly reasons that deflection implies that there must be a force on the wing, it does not explain why the air is deflected. Intuitively, one can say that the air follows the curve of the foil,^[25] but this is not very rigorous or precise.
• The theory, while correct in as far as it goes, is not sufficient to allow one to do engineering. Fluid stresses – including pressure – need to be related to the fluid motion (e.g. through constitutive equations). Thus, textbooks on aerodynamics use more complex models to provide a full description of lift.

A more rigorous physical description

Flow around an airfoil: the dots move with the flow. Note that the velocities are much higher at the upper surface than at the lower surface. The black dots are on timelines, which split into two – an upper and lower part – at the leading edge. The part of a timeline below the airfoil does not catch up with the one above. Colors of the dots indicate streamlines. The airfoil is a Kármán–Trefftz airfoil, with parameters μ_x = –0.08, μ_y = +0.08 and n = 1.94. The angle of attack is 8°, and the flow is a potential flow.

Explaining lift while considering all of the principles involved is a complex task and is not easily simplified.^[9][26] Lift is generated in accordance with the fundamental principles of physics. The most relevant physics reduce to three principles:

• Newton's laws of motion, especially Newton's second law which relates the net force on an element of air to its rate of momentum change,
• conservation of mass, including the common assumption that the airfoil's surface is impermeable for the air flowing around, and
• an expression relating the fluid stresses (consisting of pressure and shear stress components) to the properties of the flow.^[27]

In the last principle, the pressure depends on the other flow properties, such as its mass density, through the (thermodynamic) equation of state, while the shear stresses are related to the flow through the air's viscosity.^[27] Application of the viscous shear stresses to Newton's second law for an airflow results in the Navier–Stokes equations. But in many instances approximations suffice for a good description of lifting airfoils: in large parts of the flow viscosity may be neglected. Such an inviscid flow can be described mathematically through the Euler equations, resulting from the Navier-Stokes equations when the viscosity is neglected.

The Euler equations for a steady and inviscid flow can be integrated along a streamline, resulting in Bernoulli's equation. The particular form of Bernoulli's equation found depends on the equation of state used.^[28] At low Mach numbers, compressibility effects may be neglected, resulting in an incompressible flow approximation. In incompressible and inviscid flow the Bernoulli equation is just an integration of Newton's second law—in the form of the description of momentum evolution by the Euler equations—along a streamline.^[28]

In order to explain lift as it applies to an airplane wing, consider the incompressible flow around a 2-D, symmetric airfoil at positive angle of attack in a uniform freestream. Instead of considering the case where an airfoil moves through a fluid as seen by a stationary observer, it is equivalent and simpler to consider the picture when the observer follows the airfoil and the fluid moves past it.

Lift in an established flow

Streamlines around a NACA 0012 airfoil at moderate angle of attack.

If one takes the experimentally observed flow around an airfoil as a starting point, then lift can be explained in terms of pressures using Bernoulli's principle (which can be derived from Newton's second law) and conservation of mass.^[9]

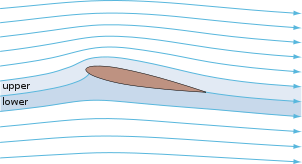
The image to the right shows the streamlines over a NACA 0012 airfoil computed using potential flow theory, a simplified model of the real flow. The flow approaching an airfoil can be divided into two streamtubes, which are defined based on the area between two streamlines. By definition, fluid never crosses a streamline in a steady flow; hence mass is conserved within each streamtube. One streamtube travels over the upper surface, while the other travels over the lower surface; dividing these two tubes is a dividing line (the stagnation streamline) that intersects the airfoil on the lower surface, typically near to the leading edge. The stagnation streamline leaves the airfoil at the sharp trailing edge, a feature of the flow known as the Kutta condition. In calculating the flow shown, the Kutta condition was imposed as an initial assumption; the justification for this assumption is explained below.

The upper stream tube constricts as it flows up and around the airfoil, a part of the so-called upwash. From the conservation of mass, the flow speed must increase as the stream tube area decreases.^[9] The area of the lower stream tube increases, causing the flow inside the tube to slow down. It is typically the case that the air parcels traveling over the upper surface will reach the trailing edge before those traveling over the bottom.

From Bernoulli's principle, the pressure on the upper surface where the flow is moving faster is lower than the pressure on the lower surface. The pressure difference thus creates a net aerodynamic force, pointing upward and downstream to the flow direction. The component of the force normal to the freestream is considered to be lift; the component parallel to the freestream is drag. In conjunction with this force by the air on the airfoil, by Newton's third law, the airfoil imparts an equal-and-opposite force on the surrounding air that creates the downwash. Measuring the momentum transferred to the downwash is another way to determine the amount of lift on the airfoil.^[29]

Flowfield formation

The last section shows that one can use Bernoulli's principle to explain lift, assuming one knows the airflow in the vicinity of the airfoil. In attempting to explain why the air flows the way it does (e.g. why the flow follows the upper surface of the airfoil and why the streamtubes change size), the situation gets considerably more complex. It is here that many simplifications are made in presenting lift to various audiences, some of which are explained after this section.

Consider the case of an airfoil accelerating from rest in a viscous flow. Lift depends entirely on the nature of viscous flow past certain bodies:^[30] in inviscid flow (i.e. assuming that viscous forces are negligible in comparison to inertial forces), there is no lift without imposing a net circulation, the proper amount of which can be determined by applying the Kutta condition. In a viscous flow like in the physical world, however, the lift and other properties arise naturally as described here.

When there is no flow, there is no lift and the forces acting on the airfoil are zero. At the instant when the flow is “turned on”, the flow is undeflected downstream of the airfoil and there are two stagnation points on the airfoil (where the flow velocity is zero): one near the leading edge on the bottom surface, and another on the upper surface near the trailing edge. The dividing line between the upper and lower streamtubes mentioned above intersects the body at the stagnation points. Since the flow speed is zero at these points, by Bernoulli's principle the static pressure at these points is at a maximum. As long as the second stagnation point is at its initial location on the upper surface of the wing, the circulation around the airfoil is zero and, in accordance with the Kutta–Joukowski theorem, there is no lift. The net pressure difference between the upper and lower surfaces is zero.

The effects of viscosity are contained within a thin layer of fluid called the boundary layer, close to the body. As flow over the airfoil commences, the flow along the lower surface turns at the sharp trailing edge and flows along the upper surface towards the upper stagnation point. The flow in the vicinity of the sharp trailing edge is very fast and the resulting viscous forces cause the boundary layer to accumulate into a vortex on the upper side of the airfoil between the trailing edge and the upper stagnation point.^[31] This is called the starting vortex. The starting vortex and the bound vortex around the surface of the wing are two halves of a closed loop. As the starting vortex increases in strength the bound vortex also strengthens, causing the flow over the upper surface of the airfoil to accelerate and drive the upper stagnation point towards the sharp trailing edge. As this happens, the starting vortex is shed into the wake,^[32] and is a necessary condition to produce lift on an airfoil. If the flow were stopped, there would be a corresponding "stopping vortex".^[33] Despite being an idealization of the real world, the “vortex system” set up around a wing is both real and observable; the trailing vortex sheet most noticeably rolls up into wing-tip vortices.

The upper stagnation point continues moving downstream until it is coincident with the sharp trailing edge (as stated by the Kutta condition). The flow downstream of the airfoil is deflected downward from the free-stream direction and, from the reasoning above in the basic explanation, there is now a net pressure difference between the upper and lower surfaces and an aerodynamic force is generated.

Other alternative explanations for the generation of lift

It is amazing that today, almost 100 years after the first flight of the Wright Flyer, groups of engineers, scientists, pilots, and others can gather together and have a spirited debate on how an airplane wing generates lift. Various explanations are put forth, and the debate centers on which explanation is the most fundamental.

— John D. Anderson, Curator of Aerodynamics at the National Air and Space Museum^[9]

Many other alternative explanations for the generation of lift by an airfoil have been put forward, of which a few are presented here. Most of them are intended to explain the phenomenon of lift to a general audience. Although the explanations may share features in common with the explanation above, additional assumptions and simplifications may be introduced. This can reduce the validity of an alternative explanation to a limited sub-class of lift generating conditions, or might not allow a quantitative analysis. Several theories introduce assumptions which proved to be wrong, like the equal transit-time theory.

"Popular" explanation based on equal transit-time

An illustration of the (incorrect) equal transit-time theory.

An explanation of lift frequently encountered in basic or popular sources is the equal transit-time theory. Equal transit-time states that because of the longer path of the upper surface of an airfoil, the air going over the top must go faster in order to catch up with the air flowing around the bottom, i.e. the parcels of air that are divided at the leading edge and travel above and below an airfoil must rejoin when they reach the trailing edge. Bernoulli's Principle is then cited to conclude that since the air moves faster on the top of the wing the air pressure must be lower. This pressure difference pushes the wing up.^[34]

However, equal transit time is not accurate^[35][36][37] and the fact that this is not generally the case can be readily observed.^[38] Although it is true that the air moving over the top of a wing generating lift does move faster, there is no requirement for equal transit time. In fact the air moving over the top of an airfoil generating lift is always moving much faster than the equal transit theory would imply.^[5]

The assertion that the air must arrive simultaneously at the trailing edge is sometimes referred to as the "Equal Transit-Time Fallacy".^{[39][40][41][42]}

Note that while this theory depends on Bernoulli's principle, the fact that this theory has been discredited does not imply that Bernoulli's principle is incorrect.

Coandă effect

Main article: Coandă effect

In a limited sense, the Coandă effect refers to the tendency of a fluid jet to stay attached to an adjacent surface that curves away from the flow, and the resultant entrainment of ambient air into the flow. The effect is named for Henri Coandă, the Romanian aerodynamicist who exploited it in many of his patents.

One of the first known uses was in his patent for a high-lift device^[43] that used a fan of gas exiting at high speed from an internal compressor. This circular spray was directed radially over the top of a curved surface shaped like a lens to decrease the pressure on that surface. The total lift for the device was caused by the difference between this pressure and that on the bottom of the craft. Two aircraft, the Antonov An-72 and An-74 "Coaler", use the exhaust from top-mounted jet engines flowing over the wing to enhance lift,^[44] as did the Boeing YC-14 and the McDonnell Douglas YC-15.^{[45] [46]} The effect is also used in high-lift devices such as a blown flap.^[47]

More broadly, some consider the effect to include the tendency of any fluid boundary layer to adhere to a curved surface, not just the boundary layer accompanying a fluid jet. It is in this broader sense that the Coandă effect is used by some to explain lift.^[48] Jef Raskin,^[49] for example, describes a simple demonstration, using a straw to blow over the upper surface of a wing. The wing deflects upwards, thus supposedly demonstrating that the Coandă effect creates lift. This demonstration correctly demonstrates the Coandă effect as a fluid jet (the exhaust from a straw) adhering to a curved surface (the wing). However, the upper surface in this flow is a complicated, vortex-laden mixing layer, while on the lower surface the flow is quiescent. The physics of this demonstration are very different from that of the general flow over the wing.^[50] The usage in this sense is encountered in some popular references on aerodynamics.^[48][49] In the aerodynamics field, the Coandă effect is commonly defined in the more limited sense above^[50][51][52] and viscosity is used to explain why the boundary layer attaches to the surface of a wing.^[33]

In terms of a difference in areas

When a fluid flows relative to a solid body, the body obstructs the flow, causing some of the fluid to change its speed and direction in order to flow around the body. The obstructive nature of the solid body causes the streamlines to move closer together in some places, and further apart in others.^[9][53][54] When fluid flows past a 2-D cambered airfoil at zero angle of attack, the upper surface has a greater area (that is, the interior area of the airfoil above the chordline) than the lower surface and hence presents a greater obstruction to the fluid than the lower surface.^[53] This asymmetry causes the streamlines in the fluid flowing over the upper surface to move closer together than the streamlines over the lower surface. As a consequence of mass conservation, the reduced area between the streamlines over the upper surface results in a higher velocity than that over the lower surface. The upper streamtube is squashed the most in the nose region ahead of the maximum thickness of the airfoil, causing the maximum velocity to occur ahead of the maximum thickness.^[9]

In accordance with Bernoulli's principle, where the fluid is moving faster the pressure is lower, and where the fluid is moving slower the pressure is greater. The fluid is moving faster over the upper surface, particularly near the leading edge, than over the lower surface so the pressure on the upper surface is lower than the pressure on the lower surface. The difference in pressure between the upper and lower surfaces results in lift.^[9]

Methods to determine lift on an airfoil

Lift coefficient

Main article: Lift coefficient

If the lift coefficient for a wing at a specified angle of attack is known (or estimated using a method such as thin-airfoil theory), then the lift produced for specific flow conditions can be determined using the following equation:^[55]

$L = \tfrac12\rho v^2 A C_L$

where

• L is lift force,
• ρ is air density
• v is true airspeed,
• A is planform area, and
• C_L is the lift coefficient at the desired angle of attack, Mach number, and Reynolds number^[56]

Kutta–Joukowski theorem

Main article: Kutta–Joukowski theorem

Lift can be calculated using potential flow theory by imposing a circulation. It is often used by practising aerodynamicists as a convenient quantity in calculations, for example thin-airfoil theory and lifting-line theory.

The circulation Γ is the line integral of the velocity of the air, in a closed loop around the boundary of an airfoil. It can be understood as the total amount of "spinning" (or vorticity) of air around the airfoil. The section lift/span L' can be calculated using the Kutta–Joukowski theorem:^[29]

$L' = \rho v \Gamma\,$

where ρ is the air density, v is the free-stream airspeed. Kelvin's circulation theorem states that circulation is conserved.^[57] There is conservation of the air's angular momentum. When an aircraft is at rest, there is no circulation.

The challenge when using the Kutta–Joukowski theorem to determine lift is to determine the appropriate circulation for a particular airfoil. In practice, this is done by applying the Kutta condition, which uniquely prescribes the circulation for a given geometry and free-stream velocity.

A physical understanding of the theorem can be observed in the Magnus effect, which is a lift force generated by a spinning cylinder in a freestream. Here the necessary circulation is induced by the mechanical rotation acting on the boundary layer, causing it to induce a faster flow around one side of the cylinder and a slower flow around the other. The asymmetric distribution of airspeed around the cylinder then produces a circulation in the outer inviscid flow.^[58]

Pressure integration

The force on the wing can be examined in terms of the pressure differences above and below the wing, which can be related to velocity changes by Bernoulli's principle.

The total lift force is the integral of vertical pressure forces over the entire wetted surface area of the wing:^[59]

$L = \oint p\mathbf{n} \cdot\mathbf{k} \; \mathrm{d}A,$

where:

• L is the lift,
• A is the wing surface area
• p is the value of the pressure,
• n is the normal unit vector pointing into the wing, and
• k is the vertical unit vector, normal to the freestream direction.

The above lift equation neglects the skin friction forces, which typically have a negligible contribution to the lift compared to the pressure forces. By using the streamwise vector i parallel to the freestream in place of k in the integral, we obtain an expression for the pressure drag D_p (which includes induced drag in a 3D wing). If we use the spanwise vector j, we obtain the side force Y.

$\begin{align} D_p &= \oint p\mathbf{n} \cdot\mathbf{i} \; \mathrm{d}A, \\[1.2ex] Y &= \oint p\mathbf{n} \cdot\mathbf{j} \; \mathrm{d}A. \end{align}$

One method for calculating the pressure is Bernoulli's equation, which is the mathematical expression of Bernoulli's principle. This method ignores the effects of viscosity, which can be important in the boundary layer and to predict friction drag, which is the other component of the total drag in addition to D_p.

The Bernoulli principle states that the sum total of energy within a parcel of fluid remains constant as long as no energy is added or removed. It is a statement of the principle of the conservation of energy applied to flowing fluids.

A substantial simplification of this proposes that as other forms of energy changes are inconsequential during the flow of air around a wing and that energy transfer in/out of the air is not significant, then the sum of pressure energy and speed energy for any particular parcel of air must be constant. Consequently, an increase in speed must be accompanied by a decrease in pressure and vice-versa. It should be noted that this is not a causational relationship. Rather, it is a coincidental relationship, whatever causes one must also cause the other as energy can neither be created nor destroyed. It is named for the Dutch-Swiss mathematician and scientist Daniel Bernoulli, though it was previously understood by Leonhard Euler and others.

Bernoulli's principle provides an explanation of pressure difference in the absence of air density and temperature variation (a common approximation for low-speed aircraft). If the air density and temperature are the same above and below a wing, a naive application of the ideal gas law requires that the pressure also be the same. Bernoulli's principle, by including air velocity, explains this pressure difference. The principle does not, however, specify the air velocity. This must come from another source, e.g., experimental data.

In order to solve for the velocity of inviscid flow around a wing, the Kutta condition must be applied to simulate the effects of viscosity. The Kutta condition allows for the correct choice among an infinite number of flow solutions that otherwise obey the laws of conservation of mass and conservation of momentum.

Lift forces on bluff bodies

Further information: Vortex shedding and Vortex-induced vibration

The flow around bluff bodies may also generate lift, besides a strong drag force. This lift may be steady, or it may oscillate due to vortex shedding. Interaction of the object's flexibility with the vortex shedding may enhance the effects of fluctuating lift and cause vortex-induced vibrations.^[60] For instance, the flow around a circular cylinder generates a Kármán vortex street: vortices being shed in an alternating fashion from each side of the cylinder. The oscillatory nature of the flow is reflected in the fluctuating lift force on the cylinder, whereas the mean lift force is negligible. The lift force frequency is characterised by the dimensionless Strouhal number, which depends (among others) on the Reynolds number of the flow.^[61][62]

For a flexible structure, this oscillatory lift force may induce vortex-induced vibrations. Under certain conditions – for instance resonance or strong spanwise correlation of the lift force – the resulting motion of the structure due to the lift fluctuations may be strongly enhanced. Such vibrations may pose problems, even collapse, in man-made tall structures like for instance industrial chimneys, if not properly taken care of in the design.^[60]

See also

• Aerodynamic force
• Banked turn
• Circulation control wing
• Downforce
• Drag (physics)
• Foil (fluid mechanics)
• Küssner effect
• Kutta condition
• Kutta–Joukowski theorem
• Lift-induced drag
• Lift-to-drag ratio
• Lifting-line theory

References and notes

1. ^ "What is Lift?". NASA Glenn Research Center. http://www.grc.nasa.gov/WWW/K-12/airplane/lift1.html. Retrieved March 4, 2009. 
2. ^ The amount of lift will be (usually slightly) more or less than gravity depending on the thrust level and vertical alignment of the thrust line. A side thrust line will result in some lift opposing side thrust as well.
3. ^ Clancy, L.J., Aerodynamics, Section 14.6
4. ^ Clancy, L.J., Aerodynamics, Section 5.2
5. ^ ^{a b} Glenn Research Center (March 15, 2006). "Incorrect Lift Theory". NASA. http://www.grc.nasa.gov/WWW/K-12/airplane/wrong1.html. Retrieved August 12, 2010. 
6. ^ "One explanation of how a wing of an airplane gives lift is that as a result of the shape of the airfoil, the air flows faster over the top than it does over the bottom because it has farther to travel. Of course, with our thin-airfoil sails, the distance along the top is the same as along the bottom so this explanation of lift fails." The Aerodynamics of Sail Interaction by Arvel Gentry Proceedings of the Third AIAA Symposium on the Aero/Hydronautics of Sailing 1971 http://www.arvelgentry.com/techs/The%20Aerodynamics%20of%20Sail%20Interaction.pdf
7. ^ "An explanation frequently given is that the path along the upper side of the aerofoil is longer and the air thus has to be faster. This explanation is wrong." A comparison of explanations of the aerodynamic lifting force Klaus Weltner Am. J. Phys. Vol.55 No.January 1, 1987
8. ^ Ison, David, "Bernoulli Or Newton: Who's Right About Lift?", Plane & Pilot, http://www.planeandpilotmag.com/component/zine/article/289.html, retrieved January 14, 2011 
9. ^ ^{a b c d e f g h} Anderson, John D. (2004), Introduction to Flight (5th ed.), McGraw-Hill, pp. 352–361, §5.19, ISBN 0-07-282569-3 
10. ^ "The wing deflects the airflow such that the mean velocity vector behind the wing is canted slightly downward (…). Hence, the wing imparts a downward component of momentum to the air; that is, the wing exerts a force on the air, pushing the flow downward. From Newton's third law, the equal and opposite reaction produces a lift." ^[9]
11. ^ Weltner, Klaus; Ingelman-Sundberg, Martin, Physics of Flight – reviewed, http://user.uni-frankfurt.de/~weltner/Flight/PHYSIC4.htm 
12. ^ "The cause of the aerodynamic lifting force is the downward acceleration of air by the airfoil... "^[11]
13. ^ "The main fact of all heaver-than-air flight is this: the wing keeps the airplane up by pushing the air down." In: Langewiesche, Wolfgang (1990), Stick and Rudder: An Explanation of the Art of Flying, McGraw-Hill, pp. 6–10, ISBN 0070362408 
14. ^ "...the effect of the wing is to give the air stream a downward velocity component. The reaction force of the deflected air mass must then act on the wing to give it an equal and opposite upward component." In: Halliday, David; Resnick, Robert, Fundamentals of Physics 3rd Edition, John Wiley & Sons, pp. 378 
15. ^ "The lift generated by an airplane is, on account of the principles of action and reaction, necessarily connected with a descending current in all its details." Ludwig Prandtl, as quoted by John D. Anderson in Introduction to Flight pg 332
16. ^ "Birds and aircraft fly because they are constantly pushing air downwards: L = dp/dt Here L is the lift force and dp/dt is the rate at which downward momentum is imparted to the airflow." Flight without Bernoulli Chris Waltham THE PHYSICS TEACHER Vol. 36, Nov. 1998 http://www.df.uba.ar/users/sgil/physics_paper_doc/papers_phys/fluids/fly_no_bernoulli.pdf
17. ^ Feynman, RichardP.; Leighton, Robert B.; Sands, Matthew (1963), The Feynman Lectures on Physics, Reading, Mass.: Addison-Wesley, ISBN 0-201-02116-1 , Vol. 1, §10–1 and §10–2.
18. ^ "Lift from Flow Turning". NASA Glenn Research Center. http://www.grc.nasa.gov/WWW/K-12/airplane/right2.html. Retrieved July 7, 2009. 
19. ^ A uniform pressure surrounding a body does not create a net force. (See buoyancy). Therefore pressure differences are needed to exert a force on a body immersed in a fluid. For example, see: Batchelor, G.K. (1967), An Introduction to Fluid Dynamics, Cambridge University Press, pp. 14–15, ISBN 0521663962 
20. ^ The Bernoulli Conundrum, February 2007, http://www.introphysics.info/Papers/BernoulliConundrumWS.pdf 
21. ^ "...if a streamline is curved, there must be a pressure gradient across the streamline..."Babinsky, Holger (November 2003), "How do wings work?", Physics Education, http://www.iop.org/EJ/article/0031-9120/38/6/001/pe3_6_001.pdf 
22. ^ NASA, Glenn Research Center. "Aerodynamic Forces". http://www.grc.nasa.gov/WWW/K-12/airplane/presar.html. Retrieved August 15, 2011. 
23. ^ "...newtonian theory is used frequently to estimate the pressure distribution of a hypersonic body." Fundamentals of Aerodynamics 3rd ed. by John D. Anderson, Jr. McGraw-Hill 2001 ISBN 0-07-237335-0 page 686
24. ^ http://www.grc.nasa.gov/WWW/K-12/airplane/wrong2.html
25. ^ Most students will be happy with the streamline pattern around a lifting wing ... because it intuitively looks right Babinsky, Holger (November 2003), "How do wings work?", Physics Education, http://www.iop.org/EJ/article/0031-9120/38/6/001/pe3_6_001.pdf 
26. ^ NASA Glenn Research Center, Bernoulli and Newton, NASA, http://www.grc.nasa.gov/WWW/K-12/airplane/bernnew.html, retrieved April 19, 2008 
27. ^ ^{a b} Batchelor, G.K. (1967), An Introduction to Fluid Dynamics, Cambridge University Press, pp. 141–151, ISBN 0521663962 
28. ^ ^{a b} Batchelor, G.K. (1967), An Introduction to Fluid Dynamics, Cambridge University Press, pp. 156–164, 265–266, 382–383, 507–509, ISBN 0521663962 
29. ^ ^{a b} Landau, L. D.; Lifshitz, E. M. (1987), Fluid mechanics, Course of Theoretical Physics, 6 (2nd revised ed.), Pergamon Press, ISBN 0 08 033932 8, OCLC 15017127 , pp. 68–69 and pp. 153–155.
30. ^ Karamacheti, Krishnamurty (1980), Principles of Ideal-Fluid Aerodynamics (Reprint ed.), Robert E. Krieger 
31. ^ Clancy, L.J., Aerodynamics, Figure 4.7
32. ^ Clancy, L.J., Aerodynamics, Figure 4.8
33. ^ ^{a b} White, Frank M. (2002), Fluid Mechanics (5th ed.), McGraw Hill 
34. ^ "The airfoil of the airplane wing, according to the textbook explanation that is more or less standard in the United States, has a special shape with more curvature on top than on the bottom; consequently, the air must travel farther over the top surface than over the bottom surface. Because the air must make the trip over the top and bottom surfaces in the same elapsed time ..., the velocity over the top surface will be greater than over the bottom. According to Bernoulli's theorem, this velocity difference produces a pressure difference which is lift." Bernoulli and Newton in Fluid Mechanics Norman F. Smith The Physics Teacher November 1972 Volume 10, Issue 8, pp. 451 http://tpt.aapt.org/resource/1/phteah/v10/i8
35. ^ "Unfortunately, this explanation falls to earth on three counts. First, an airfoil need not have more curvature on its top than on its bottom. Airplanes can and do fly with perfectly symmetrical airfoils; that is with airfoils that have the same curvature top and bottom. Second, even if a humped-up (cambered) shape is used, the claim that the air must traverse the curved top surface in the same time as it does the flat bottom surface...is fictional. We can quote no physical law that tells us this. Third – and this is the most serious – the common textbook explanation, and the diagrams that accompany it, describe a force on the wing with no net disturbance to the airstream. This constitutes a violation of Newton's third law." Bernoulli and Newton in Fluid Mechanics Norman F. Smith The Physics Teacher November 1972 Volume 10, Issue 8, pp. 451 http://tpt.aapt.org/resource/1/phteah/v10/i8
36. ^ Anderson, David (2001), Understanding Flight, New York: McGraw-Hill, pp. 15–16, ISBN 0071363777, "The first thing that is wrong is that the principle of equal transit times is not true for a wing with lift." 
37. ^ "This is simply not true." Anderson, John D. Jr, Introduction to Flight, p.355 (5th edition), McGraw-Hill ISBN 0-07-282569-3
38. ^ Flow Visualization. National Committee for Fluid Mechanics Films/Educational Development Center. http://web.mit.edu/hml/ncfmf.html. Retrieved January 21, 2009.  A visualization of the typical retarded flow over the lower surface of the wing and the accelerated flow over the upper surface starts at 5:29 in the video.
39. ^ A false explanation for lift has been put forward in mainstream books, and even in scientific exhibitions. Known as the "equal transit-time" explanation, it states that the parcels of air which are divided by an airfoil must rejoin again; because of the greater curvature (and hence longer path) of the upper surface of an aerofoil, the air going over the top must go faster in order to "catch up" with the air flowing around the bottom. Therefore, because of its higher speed the pressure of the air above the airfoil must be lower. Despite the fact that this "explanation" is probably the most common of all, it is false. It has recently been dubbed the "Equal transit-time fallacy.""Fixed wing aircraft facts and how aircraft fly". http://www.aviationexplorer.com/fixed_wing_aircraft.htm. Retrieved July 7, 2009. 
40. ^ ...it leaves the impression that Professor Bernoulli is somehow to blame for the "equal transit time" fallacy... John S. Denker (1999). "Critique of "How Airplanes Fly"". http://www.av8n.com/fly/lift.htm. Retrieved July 7, 2009. 
41. ^ The fallacy of equal transit time can be deduced from consideration of a flat plate, which will indeed produce lift, as anyone who has handled a sheet of plywood in the wind can testify.Gale M. Craig. "Physical principles of winged flight". http://regenpress.com/. Retrieved July 7, 2009. 
42. ^ Fallacy 1: Air takes the same time to move across the top of an aerofoil as across the bottom.Peter Eastwell (2007), "Bernoulli? Perhaps, but What About Viscosity?", The Science Education Review 6 (1), http://www.scienceeducationreview.com/open_access/eastwell-bernoulli.pdf, retrieved July 14, 2009. 
43. ^ US 2108652 
44. ^ Antonov, Oleg Konstantinovich (24-May), http://www.aviation.ru/An 
45. ^ Neely, Mike (2008), http://www.theaviationzone.com/factsheets/amst.asp, retrieved 21-July-2008 
46. ^ Pike, John (2008), GlobalSecurity.org, http://www.globalsecurity.org/military/systems/aircraft/c-14.htm, retrieved 23-July-2008 
47. ^ Englar, Robert J. (June 2005), "Overview of Circulation Control Pneumatic Aerodynamics: Blown Force and Moment Augmentation and Modification as Applied Primarily to Fixed-Wing Aircraft", Proceedings of the 2004 NASA/ONR Circulation Control Workshop, Part 1, NASA/ONR, pp. 37–99 
48. ^ ^{a b} Anderson, David; Eberhart, Scott (1999), How Airplanes Fly: A Physical Description of Lift, http://www.allstar.fiu.edu/AERO/airflylvl3.htm, retrieved June 4, 2008 
49. ^ ^{a b} Raskin, Jef (1994), Coanda Effect: Understanding Why Wings Work, archived from the original on September 28, 2007, http://web.archive.org/web/20070928072421/http://jef.raskincenter.org/published/coanda_effect.html 
50. ^ ^{a b} Auerbach, David (2000), "Why Aircraft Fly", Eur. J. Phys. 21 (4): 289–296, Bibcode 2000EJPh...21..289A, doi:10.1088/0143-0807/21/4/302 
51. ^ Denker, JS, Fallacious Model of Lift Production, http://www.av8n.com/how/htm/spins.html#sec-coanda-fallacy, retrieved 2008-08-18 
52. ^ Wille, R; Fernholz, H (1965), "Report on the first European Mechanics Colloquium, on the Coanda effect", J. Fluid Mech. 23 (4): 801–819, Bibcode 1965JFM....23..801W, doi:10.1017/S0022112065001702, http://journals.cambridge.org/action/displayAbstract?fromPage=online&aid=370712 
53. ^ ^{a b} Smith, Hubert (1992), Illustrated Guide to Aerodynamics, McGraw-Hill Professional, pp. 17–23, ISBN 0830639012 
54. ^ Brandt, Steven A.; Stiles, Randall J. (2004), Introduction to Aeronautics: A Design Perspective, AIAA, p. 74, ISBN 1563477017 
55. ^ Anderson, John D. (2004), Introduction to Flight (5th ed.), McGraw-Hill, pp. 257–261, ISBN 0-07-282569-3 
56. ^ Yoon, Joe (2003-12-28), Mach Number & Similarity Parameters, Aerospaceweb.org, http://www.aerospaceweb.org/question/aerodynamics/q0156.shtml, retrieved 2009-02-11 
57. ^ Clancy, L.J., Aerodynamics, Section 7.27
58. ^ Clancy, L.J., Aerodynamics, Sections 4.5 and 4.6
59. ^ Anderson, John D. (2004), Introduction to Flight, Section 5.7 (5th edition), McGraw-Hill. ISBN 0-07-282569-3
60. ^ ^{a b} Williamson, C.H.K.; Govardhan, R. (2004), "Vortex-induced vibrations", Annual Review of Fluid Mechanics 36: 413–455, Bibcode 2004AnRFM..36..413W, doi:10.1146/annurev.fluid.36.050802.122128 
61. ^ Sumer, B. Mutlu; Fredsøe, Jørgen (2006), Hydrodynamics around cylindrical structures (revised ed.), World Scientific, pp. 6–13, 42–45 & 50–52, ISBN 9812700390 
62. ^ Zdravkovich, M.M. (2003), Flow around circular cylinders, 2, Oxford University Press, pp. 850–855, ISBN 0198565615 

Further reading

• Introduction to Flight, John D. Anderson, Jr., McGraw-Hill, ISBN 0-07-299071-6 – The author is the Curator of Aerodynamics at the Smithsonian Institution's National Air & Space Museum and Professor Emeritus at the University of Maryland.

• Understanding Flight, by David Anderson and Scott Eberhardt, McGraw-Hill, ISBN 0-07-136377-7 – The authors are a physicist and an aeronautical engineer. They explain flight in non-technical terms and specifically address the equal-transit-time myth. Turning of the flow around the wing is attributed to the Coanda effect, which is quite controversial.

• Aerodynamics, Clancy, L.J. (1975), Section 4.8, Pitman Publishing Limited, London ISBN 0 273 01120 0.

• Aerodynamics, Aeronautics, and Flight Mechanics, McCormick, Barnes W., (1979), Chapter 3, John Wiley & Sons, Inc., New York ISBN 0-471-03032-5.

• Fundamentals of Flight, Richard S. Shevell, Prentice-Hall International Editions, ISBN 0-13-332917-8 – This book is primarily intended as a text for a one semester undergraduate course in mechanical or aeronautical engineering, although its sections on theory of flight are understandable with a passing knowledge of calculus and physics.

• "Observation of Perfect Potential Flow in Superfluid", Paul P. Craig and John R. Pellam (1957) Physical Review 108(5), pp. 1109–1112, doi:10.1103/PhysRev.108.1109 – Experiments under superfluidity conditions, resulting in the vanishing of lift in inviscid flow since the Kutta condition no longer is satisfied.

• "Flight without Bernoulli" Chris Waltham Vol. 36, Nov. 1998 THE PHYSICS TEACHER – using a physical model relying only on Newton’s second law, the author presents a rigorous fluid dynamical treatment of flight. http://www.df.uba.ar/users/sgil/physics_paper_doc/papers_phys/fluids/fly_no_bernoulli.pdf

• "Bernoulli and Newton in Fluid Mechanics" Norman F. Smith The Physics Teacher November 1972 Volume 10, Issue 8, pp. 451 – Original paper criticizing the "popular" explanation of lift and explaining it in terms of Newton's laws http://tpt.aapt.org/resource/1/phteah/v10/i8

External links

• Discussion of the apparent "conflict" between the various explanations of lift
• NASA tutorial, with animation, describing lift
• Explanation of Lift with animation of fluid flow around an airfoil
• A treatment of why and how wings generate lift that focuses on pressure.
• Physics of Flight – reviewed. Online paper by Prof. Dr. Klaus Weltner.
• How do Wings Work? – Holger Babinsky