- Phase-locked loop
-
"PLL" redirects here. For other uses, see PLL (disambiguation).
A phase-locked loop or phase lock loop (PLL) is a control system that generates an output signal whose phase is related to the phase of an input "reference" signal. It is an electronic circuit consisting of a variable frequency oscillator and a phase detector. This circuit compares the phase of the input signal with the phase of the signal derived from its output oscillator and adjusts the frequency of its oscillator to keep the phases matched. The signal from the phase detector is used to control the oscillator in a feedback loop.
Frequency is the derivative of phase. Keeping the input and output phase in lock step implies keeping the input and output frequencies in lock step. Consequently, a phase-locked loop can track an input frequency, or it can generate a frequency that is a multiple of the input frequency. The former property is used for demodulation, and the latter property is used for indirect frequency synthesis.
Phase-locked loops are widely employed in radio, telecommunications, computers and other electronic applications. They can be used to recover a signal from a noisy communication channel, generate stable frequencies at a multiple of an input frequency (frequency synthesis), or distribute clock timing pulses in digital logic designs such as microprocessors. Since a single integrated circuit can provide a complete phase-locked-loop building block, the technique is widely used in modern electronic devices, with output frequencies from a fraction of a hertz up to many gigahertz.
Contents
Practical analogies
Automobile race analogy
For a practical idea of what is going on, consider an auto race. There are many cars, and each of them wants to go around the track as fast as possible. Each lap corresponds to a complete cycle, and each car will complete dozens of laps per hour. The number of laps per hour (a speed) corresponds to an angular velocity (i.e. a frequency), but the number of laps (a distance) corresponds to a phase (and the conversion factor is the distance around the track loop).
During most of the race, each car is on its own and is trying to beat every other car on the course, and the phase of each car varies freely.
However, if there is an accident, a pace car comes out to set a safe speed. None of the race cars are permitted to pass the pace car (or the race cars in front of them), but each of the race cars wants to stay as close to the pace car as it can. While it is on the track, the pace car is a reference, and the race cars become phase-locked loops. Each driver will measure the phase difference (a distance in laps) between him and the pace car. If the driver is far away, he will increase his engine speed to close the gap. If he's too close to the pace car, he will slow down. The result is all the race cars lock on to the phase of the pace car. The cars travel around the track in a tight group that is a small fraction of a lap.
Clock analogy
Phase can be proportional to time,[1] so a phase difference can be a time difference. Clocks are, with varying degrees of accuracy, phase-locked (time-locked) to a master clock.
Left on its own, each clock will mark time at slightly different rates. A wall clock, for example, might be fast by a few seconds per hour compared to the reference clock at NIST. Over time, that time difference would become substantial.
To keep his clock in synch, each week the owner compares the time on his wall clock to a more accurate clock (a phase comparison), and he resets his clock. Left alone, the wall clock will continue to diverge from the reference clock at the same few seconds per hour rate.
Some clocks have a timing adjustment (a fast-slow control). When the owner compared his wall clock's time to the reference time, he noticed that his clock was too fast. Consequently, he could turn the timing adjust a small amount to make the clock run a little slower. If things work out right, his clock will be more accurate. Over a series of weekly adjustments, the wall clock's notion of a second would agree with the reference time (within the wall clock's stability).
An early mechanical version of a phase-locked loop was used in 1921 in the Shortt-Synchronome clock.
History
Automatic synchronization of electronic oscillators was described in 1923.[2] Earliest research towards what became known as the phase-locked loop goes back to 1932, when British researchers developed an alternative to Edwin Armstrong's superheterodyne receiver, the Homodyne or direct-conversion receiver. In the homodyne or synchrodyne system, a local oscillator was tuned to the desired input frequency and multiplied with the input signal. The resulting output signal included the original modulation information. The intent was to develop an alternative receiver circuit that required fewer tuned circuits than the superheterodyne receiver. Since the local oscillator would rapidly drift in frequency, an automatic correction signal was applied to the oscillator, maintaining it in the same phase and frequency as the desired signal. The technique was described in 1932, in a paper by Henri de Bellescize, in the French journal L'Onde Électrique.[3][4][5]
In analog television receivers since at least the late 1930s, phase-locked-loop horizontal and vertical sweep circuits are locked to synchronization pulses in the broadcast signal.[6]
When Signetics introduced a line of monolithic integrated circuits that were complete phase-locked loop systems on a chip in 1969,[7] applications for the technique multiplied. A few years later RCA introduced the "CD4046" CMOS Micropower Phase-Locked Loop, which became a popular integrated circuit.
Structure and function
Phase-locked loop mechanisms may be implemented as either analog or digital circuits. Both implementations use the same basic structure. Both analog and digital PLL circuits include four basic elements:
- Phase detector,
- Low-pass filter,
- Variable-frequency oscillator, and
- feedback path (which may include a frequency divider).
Variations
There are several variations of PLLs. Some terms that are used are analog phase-locked loop (APLL) also referred to as a linear phase-locked loop (LPLL), digital phase-locked loop (DPLL), all digital phase-locked loop (ADPLL), and software phase-locked loop (SPLL).[8]
- Analog or Linear PLL (LPLL)
- Phase detector is an analog multiplier. Loop filter is active or passive. Uses a Voltage-controlled oscillator (VCO).
- Digital PLL (DPLL)
- An analog PLL with a digital phase detector (such as XOR, edge-trigger JK, phase frequency detector). May have digital divider in the loop.
- All digital PLL (ADPLL)
- Phase detector, filter and oscillator are digital. Uses a numerically controlled oscillator (NCO).
- Software PLL (SPLL)
- Functional blocks are implemented by software rather than specialized hardware.
Performance parameters
- Type and order
- Lock range: The frequency range the PLL is able to stay locked. Mainly defined by the VCO range.
- Capture range: The frequency range the PLL is able to lock-in, starting from unlocked condition. This range is usually smaller than the lock range and will depend e.g. on phase detector.
- Loop bandwidth: Defining the speed of the control loop.
- Transient response: Like overshoot and settling time to a certain accuracy (like 50ppm).
- Steady-state errors: Like remaining phase or timing error
- Output spectrum purity: Like sidebands generated from a certain VCO tuning voltage ripple.
- Phase-noise: Defined by noise energy in a certain frequency band (like 10kHz offset from carrier). Highly dependent on VCO phase-noise, PLL bandwidth, etc.
- General parameters: Such as power consumption, supply voltage range, output amplitude, etc.
Applications
Phase-locked loops are widely used for synchronization purposes; in space communications for coherent demodulation and threshold[disambiguation needed
 ] extension, bit synchronization, and symbol synchronization. Phase-locked loops can also be used to demodulate frequency-modulated signals. In radio transmitters, a PLL is used to synthesize new frequencies which are a multiple of a reference frequency, with the same stability as the reference frequency.
] extension, bit synchronization, and symbol synchronization. Phase-locked loops can also be used to demodulate frequency-modulated signals. In radio transmitters, a PLL is used to synthesize new frequencies which are a multiple of a reference frequency, with the same stability as the reference frequency.Other applications include:
- Demodulation of both FM and AM signals
- Recovery of small signals that otherwise would be lost in noise (lock-in amplifier)
- Recovery of clock timing information from a data stream such as from a disk drive
- Clock multipliers in microprocessors that allow internal processor elements to run faster than external connections, while maintaining precise timing relationships
- DTMF decoders, modems, and other tone decoders, for remote control and telecommunications
Clock recovery
Some data streams, especially high-speed serial data streams (such as the raw stream of data from the magnetic head of a disk drive), are sent without an accompanying clock. The receiver generates a clock from an approximate frequency reference, and then phase-aligns to the transitions in the data stream with a PLL. This process is referred to as clock recovery. In order for this scheme to work, the data stream must have a transition frequently enough to correct any drift in the PLL's oscillator. Typically, some sort of redundant encoding is used, such as 8b/10b encoding.
Deskewing
If a clock is sent in parallel with data, that clock can be used to sample the data. Because the clock must be received and amplified before it can drive the flip-flops which sample the data, there will be a finite, and process-, temperature-, and voltage-dependent delay between the detected clock edge and the received data window. This delay limits the frequency at which data can be sent. One way of eliminating this delay is to include a deskew PLL on the receive side, so that the clock at each data flip-flop is phase-matched to the received clock. In that type of application, a special form of a PLL called a delay-locked loop (DLL) is frequently used.[9]
Clock generation
Many electronic systems include processors of various sorts that operate at hundreds of megahertz. Typically, the clocks supplied to these processors come from clock generator PLLs, which multiply a lower-frequency reference clock (usually 50 or 100 MHz) up to the operating frequency of the processor. The multiplication factor can be quite large in cases where the operating frequency is multiple gigahertz and the reference crystal is just tens or hundreds of megahertz.
Spread spectrum
All electronic systems emit some unwanted radio frequency energy. Various regulatory agencies (such as the FCC in the United States) put limits on the emitted energy and any interference caused by it. The emitted noise generally appears at sharp spectral peaks (usually at the operating frequency of the device, and a few harmonics). A system designer can use a spread-spectrum PLL to reduce interference with high-Q receivers by spreading the energy over a larger portion of the spectrum. For example, by changing the operating frequency up and down by a small amount (about 1%), a device running at hundreds of megahertz can spread its interference evenly over a few megahertz of spectrum, which drastically reduces the amount of noise seen on broadcast FM radio channels, which have a bandwidth of several tens of kilohertz.
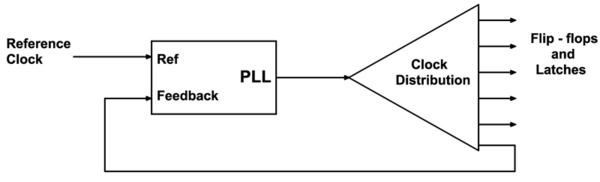
Clock distribution
Typically, the reference clock enters the chip and drives a phase locked loop (PLL), which then drives the system's clock distribution. The clock distribution is usually balanced so that the clock arrives at every endpoint simultaneously. One of those endpoints is the PLL's feedback input. The function of the PLL is to compare the distributed clock to the incoming reference clock, and vary the phase and frequency of its output until the reference and feedback clocks are phase and frequency matched.
PLLs are ubiquitous—they tune clocks in systems several feet across, as well as clocks in small portions of individual chips. Sometimes the reference clock may not actually be a pure clock at all, but rather a data stream with enough transitions that the PLL is able to recover a regular clock from that stream. Sometimes the reference clock is the same frequency as the clock driven through the clock distribution, other times the distributed clock may be some rational multiple of the reference.
Jitter and noise reduction
One desirable property of all PLLs is that the reference and feedback clock edges be brought into very close alignment. The average difference in time between the phases of the two signals when the PLL has achieved lock is called the static phase offset (also called the steady-state phase error). The variance between these phases is called tracking jitter. Ideally, the static phase offset should be zero, and the tracking jitter should be as low as possible.[dubious ]
Phase noise is another type of jitter observed in PLLs, and is caused by the oscillator itself and by elements used in the oscillator's frequency control circuit. Some technologies are known to perform better than others in this regard. The best digital PLLs are constructed with emitter-coupled logic (ECL) elements, at the expense of high power consumption. To keep phase noise low in PLL circuits, it is best to avoid saturating logic families such as transistor-transistor logic (TTL) or CMOS.[citation needed]
Another desirable property of all PLLs is that the phase and frequency of the generated clock be unaffected by rapid changes in the voltages of the power and ground supply lines, as well as the voltage of the substrate on which the PLL circuits are fabricated. This is called substrate and supply noise rejection. The higher the noise rejection, the better.
To further improve the phase noise of the output, an injection locked oscillator can be employed following the VCO in the PLL.
Frequency Synthesis
In digital wireless communication systems (GSM, CDMA etc.), PLLs are used to provide the local oscillator for up-conversion during transmission and down-conversion during reception. In most cellular handsets this function has been largely integrated into a single integrated circuit to reduce the cost and size of the handset. However, due to the high performance required of base station terminals, the transmission and reception circuits are built with discrete components to achieve the levels of performance required. GSM local oscillator modules are typically built with a frequency synthesizer integrated circuit and discrete resonator VCOs.[citation needed]
Frequency synthesizer manufacturers include Analog Devices,[10] National Semiconductor and Texas Instruments. VCO manufacturers include Sirenza, Z-Communications, Inc. (Z-COMM).
Phase-locked loop block diagram
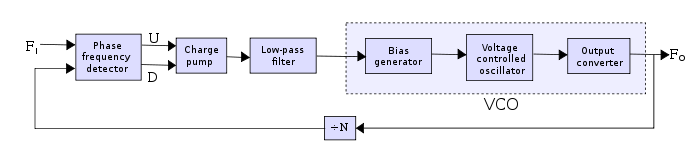 Digital phase-locked loop block diagram
Digital phase-locked loop block diagram
A phase detector compares two input signals and produces an error signal which is proportional to their phase difference. The error signal is then low-pass filtered and used to drive a VCO which creates an output phase. The output is fed through an optional divider back to the input of the system, producing a negative feedback loop. If the output phase drifts, the error signal will increase, driving the VCO phase in the opposite direction so as to reduce the error. Thus the output phase is locked to the phase at the other input. This input is called the reference.
Analog phase locked loops are generally built with an analog phase detector, low pass filter and VCO placed in a negative feedback configuration. A digital phase locked loop uses a digital phase detector; it may also have a divider in the feedback path or in the reference path, or both, in order to make the PLL's output signal frequency a rational multiple of the reference frequency. A non-integer multiple of the reference frequency can also be created by replacing the simple divide-by-N counter in the feedback path with a programmable pulse swallowing counter. This technique is usually referred to as a fractional-N synthesizer or fractional-N PLL.[dubious ]
The oscillator generates a periodic output signal. Assume that initially the oscillator is at nearly the same frequency as the reference signal. If the phase from the oscillator falls behind that of the reference, the phase detector changes the control voltage of the oscillator so that it speeds up. Likewise, if the phase creeps ahead of the reference, the phase detector changes the control voltage to slow down the oscillator. Since initially the oscillator may be far from the reference frequency, practical phase detectors may also respond to frequency differences, so as to increase the lock-in range of allowable inputs.
Depending on the application, either the output of the controlled oscillator, or the control signal to the oscillator, provides the useful output of the PLL system.
Elements
Phase detector
Main article: phase detectorThe two inputs of the phase detector are the reference input and the feedback from the VCO. The PD output controls the VCO such that the phase difference between the two inputs is held constant, making it a negative feedback system. There are several types of phase detectors in the two main categories of analog and digital.
Different types of phase detectors have different performance characteristics.
For instance, the frequency mixer produces harmonics that adds complexity in applications where spectral purity of the VCO signal is important. The resulting unwanted (spurious) sidebands, also called "reference spurs" can dominate the filter requirements and reduce the capture range and lock time well below the requirements. In these applications the more complex digital phase detectors are used which do not have as severe a reference spur component on their output. Also, when in lock, the steady-state phase difference at the inputs using this type of phase detector is near 90 degrees. The actual difference is determined by the DC loop gain.
A bang-bang charge pump phase detector must always have a dead band where the phases of inputs are close enough that the detector detects no phase error. For this reason, bang-bang phase detectors are associated with significant minimum peak-to-peak jitter, because of drift within the dead band.[citation needed] However these types, having outputs consisting of very narrow pulses at lock, are very useful for applications requiring very low VCO spurious outputs. The narrow pulses contain very little energy and are easy to filter out of the VCO control voltage. This results in low VCO control line ripple and therefore low FM sidebands on the VCO.[citation needed]
In PLL applications it is frequently required to know when the loop is out of lock. The more complex digital phase-frequency detectors usually have an output that allows a reliable indication of an out of lock condition.
Filter
The block commonly called the PLL loop filter (usually a low pass filter) generally has two distinct functions.
The primary function is to determine loop dynamics, also called stability. This is how the loop responds to disturbances, such as changes in the reference frequency, changes of the feedback divider, or at startup. Common considerations are the range over which the loop can achieve lock (pull-in range, lock range or capture range), how fast the loop achieves lock (lock time, lock-up time or settling time) and damping behavior. Depending on the application, this may require one or more of the following: a simple proportion (gain or attenuation), an integral (low pass filter) and/or derivative (high pass filter). Loop parameters commonly examined for this are the loop's gain margin and phase margin. Common concepts in control theory including the PID controller are used to design this function.
The second common consideration is limiting the amount of reference frequency energy (ripple) appearing at the phase detector output that is then applied to the VCO control input. This frequency modulates the VCO and produces FM sidebands commonly called "reference spurious". The low pass characteristic of this block can be used to attenuate this energy, but at times a band reject "notch" may also be useful.[citation needed]
The design of this block can be dominated by either of these considerations, or can be a complex process juggling the interactions of the two. Typical trade-offs are: increasing the bandwidth usually degrades the stability or too much damping for better stability will reduce the speed and increase settling time. Often also the phase-noise is affected.
Oscillator
Main article: Electronic oscillatorAll phase-locked loops employ an oscillator element with variable frequency capability. This can be an analog VCO either driven by analog circuitry in the case of an APLL or driven digitally through the use of a digital-to-analog converter as is the case for some DPLL designs. Pure digital oscillators such as a numerically controlled oscillator are used in ADPLLs.
Feedback path and optional divider
PLLs may include a divider between the oscillator and the feedback input to the phase detector to produce a frequency synthesizer. A programmable divider is particularly useful in radio transmitter applications, since a large number of transmit frequencies can be produced from a single stable, accurate, but expensive, quartz crystal–controlled reference oscillator.
Some PLLs also include a divider between the reference clock and the reference input to the phase detector. If the divider in the feedback path divides by N and the reference input divider divides by M, it allows the PLL to multiply the reference frequency by N / M. It might seem simpler to just feed the PLL a lower frequency, but in some cases the reference frequency may be constrained by other issues, and then the reference divider is useful.
Frequency multiplication in a sense can also be attained by locking the PLL to the 'N'th harmonic of the signal.[clarification needed]
It should also be noted that the feedback is not limited to a frequency divider. This element can be other elements such as a frequency multiplier, or a mixer. The multiplier will make the VCO output a sub-multiple (rather than a multiple) of the reference frequency. A mixer can translate the VCO frequency by a fixed offset. It may also be a combination of these. An example being a divider following a mixer; this allows the divider to operate at a much lower frequency than the VCO without a loss in loop gain.
Modeling
Time domain model
The equations governing a phase-locked loop with an analog multiplier as the phase detector and linear filter may be derived as follows. Let the input to the phase detector be xr(θr(t)) and the output of the VCO is xc(θc(t)) with phases θr(t) and θc(t). Functions xc(θ) and xr(θ) describe waveforms of signals. Then the output of the phase detector xm(t) is given by
- xm(t) = xr(θr(t))xc(θc(t))
the VCO frequency is usually taken as a function of the VCO input g(t) as
where gv is the sensitivity of the VCO and is expressed in Hz / V; ωc is a free-running frequency of VCO.
The Loop Filter can be described by system of linear differential equations
where xm(t) is an input of the filter, xf(t) is an output of the filter, A is n-by-n matrix,
 .
.  represents an initial state of the filter. The star symbol is a conjugate transpose.
represents an initial state of the filter. The star symbol is a conjugate transpose.Hence the following system describes PLL
where φ0 is an initial phase shift.
Phase domain model
Consider the input of pll xr(θr(t)) and VCO output xc(θc(t)) are high frequency signals. Then for any piecewise differentiable 2π-periodic functions xr(θ) and xc(θ) there is a function φ(θ) such that the output G(t) of Filter
in phase domain is assymptotically equal ( the difference G(t) − xf(t) is small with respect to the frequencies) to the output of the Filter in time domain model. [11] [12] Here function φ(θ) is a Phase Detector characteristic.
Denote by θe(t) the phase difference
- θe = θr(t) − θc(t).
Then the following dynamical system describes PLL behavior
Here ωe = ωr − ωc; ωr is a frequency of reference oscillator( we assume that ωr is constant).
Example
Consider sinusoidal signals
and simple one-pole RC circuit as a filter. Time domain model takes form
PD characteristics for this signals is equal[13] to
Hence the phase domain model takes form
This system of equations is equivalent to the equation of mathematical pendulum
Linearized phase domain model
Phase locked loops can also be analyzed as control systems by applying the Laplace transform. The loop response can be written as:
Where
- θo is the output phase in radians
- θi is the input phase in radians
- Kp is the phase detector gain in volts per radian
- Kv is the VCO gain in radians per volt-second
- F(s) is the loop filter transfer function (dimensionless)
The loop characteristics can be controlled by inserting different types of loop filters. The simplest filter is a one-pole RC circuit. The loop transfer function in this case is:
The loop response becomes:
This is the form of a classic harmonic oscillator. The denominator can be related to that of a second order system:
Where
- ζ is the damping factor
- ωn is the natural frequency of the loop
For the one-pole RC filter,
The loop natural frequency is a measure of the response time of the loop, and the damping factor is a measure of the overshoot and ringing. Ideally, the natural frequency should be high and the damping factor should be near 0.707 (critical damping). With a single pole filter, it is not possible to control the loop frequency and damping factor independently. For the case of critical damping,
A slightly more effective filter, the lag-lead filter includes one pole and one zero. This can be realized with two resistors and one capacitor. The transfer function for this filter is
This filter has two time constants
- τ1 = C(R1 + R2)
- τ2 = CR2
Substituting above yields the following natural frequency and damping factor
The loop filter components can be calculated independently for a given natural frequency and damping factor
Real world loop filter design can be much more complex e.g. using higher order filters to reduce various types or source of phase noise. (See the D Banerjee ref below)
See also
- Control theory
- Direct-digital synthesis
- Costas loop
- Kalman filter
- Direct conversion receiver
- Circle map - a simple mathematical model of the phase-locked loop showing both mode-locking and chaotic behavior.
- Carrier recovery
- Delay-locked loop (DLL)
- PLL multibit
References
- ^ If the frequency is constant and the initial phase is zero, then the phase of a sinusoid is proportional to time.
- ^ E. V. Appleton, Automatic synchronization of triode oscillators, Proc. Cambridge Phil. Soc., 21(Part III):231 (1922-1923)
- ^ Henri de Bellescize, "La réception synchrone," L'Onde Électrique (later: Revue de l'Electricité et de l'Electronique), vol. 11, pages 230-240 (June 1932).
- ^ See also: French patent no. 635,451 (filed: 6 October 1931; issued: 29 September 1932); and U.S. patent "Synchronizing system," no. 1,990,428 (filed: 29 September 1932; issued: 5 February 1935).
- ^ Notes for a University of Guelph course describing the PLL and early history, including an IC PLL tutorial[dead link]
- ^ "National Television Systems Committee Video Display Signal IO". Sxlist.com. http://www.sxlist.com/techref/io/video/ntsc.htm. Retrieved 2010-10-14.
- ^ A. B. Grebene, H. R. Camenzind, “Phase Locking As A New Approach For Tuned Integrated Circuits”, ISSCC Digest of Technical Papers, pp. 100-101, Feb. 1969.
- ^ Roland E. Best (2007). Phase-Locked Loops: Design, Simulation and Applications (6th ed.). McGraw Hill. ISBN 978-0-07-149375-8.
- ^ M Horowitz, C. Yang, S. Sidiropoulos (1998-01-01). "High-speed electrical signaling: overview and limitations". IEEE Micro. http://www-vlsi.stanford.edu/papers/mh_micro_98.pdf.
- ^ "PLL Synthesizers/VCOs". Analog Devices. http://www.analog.com/en/rfif-components/pll-synthesizersvcos/products/index.html. Retrieved 2010-10-14.
- ^ G. A. Leonov, N. V. Kuznetsov, M. V. Yuldashev, R. V. Yuldashev (2011). "Computation of Phase Detector Characteristics in Synchronization Systems". Doklady Mathematics 84 (1): 586–590. doi:10.1134/S1064562411040223.
- ^ N.V. Kuznetsov, G.A. Leonov, M.V. Yuldashev, R.V. Yuldashev (2011). "Analytical methods for computation of phase-detector characteristics and PLL design". ISSCS 2011 - International Symposium on Signals, Circuits and Systems, Proceedings: 7–10. doi:10.1109/ISSCS.2011.5978639.
- ^ A. J. Viterbi, Principles of Coherent Communication, McGraw-Hill, New York, 1966
Further reading
- Banerjee, Dean (2006), PLL Performance, Simulation and Design Handbook (4th ed.), National Semiconductor, http://www.national.com/analog/timing/pll_designbook. (PDF version).
- Best, R. E. (2003), Phase-locked Loops: Design, Simulation and Applications, McGraw-Hill, ISBN 0-07-141201-8
- de Bellescize, Henri (June 1932), "La réception Synchrone", L'Onde Electrique 11: 230–240
- Dorf, Richard C. (1993), The Electrical Engineering Handbook, Boca Raton: CRC Press, ISBN 0-8493-0185-8
- Egan, William F. (1998), Phase-Lock Basics, John Wiley & Sons. (provides useful Matlab scripts for simulation)
- Egan, William F. (2000), Frequency Synthesis by Phase Lock (2nd ed.), John Wiley and Sons. (provides useful Matlab scripts for simulation)
- Gardner, Floyd M. (2005), Phaselock Techniques (3rd ed.), Wiley-Interscience, ISBN 978-0471430636
- Klapper, J.; Frankle, J. T. (1972), Phase-Locked and Frequency-Feedback Systems, Academic Press. (FM Demodulation)
- Kundert, Ken (August 2006), Predicting the Phase Noise and Jitter of PLL-Based Frequency Synthesizers (4g ed.), Designer's Guide Consulting, Inc., http://www.designers-guide.org/Analysis/PLLnoise+jitter.pdf
- Liu, Mingliang (February 21, 2006), Build a 1.5-V 2.4-GHz CMOS PLL, Wireless Net Design Line, http://www.wirelessnetdesignline.com/howto/180205535. An article on designing a standard PLL IC for Bluetooth applications.
- Wolaver, Dan H. (1991), Phase-Locked Loop Circuit Design, Prentice Hall, ISBN 0136627439
- Signal processing and system aspects of all-digital phase-locked loops (ADPLLs), http://www2.spsc.tugraz.at/people/cvogel/ADPLL.html
Categories:- Oscillators
- Communication circuits
- Electronic design
- Radio electronics
Wikimedia Foundation. 2010.