Curve

For other uses, see Curve (disambiguation).

A parabola, a simple example of a curve

In mathematics, a curve (also called a curved line in older texts) is, generally speaking, an object similar to a line but which is not required to be straight. This entails that a line is a special case of curve, namely a curve with null curvature.^[1] Often curves in two-dimensional (plane curves) or three-dimensional (space curves) Euclidean space are of interest.

Different disciplines within mathematics have given the term different meanings depending on the area of study, so the precise meaning depends on context. However many of these meanings are special instances of the definition which follows. A curve is a topological space which is locally homeomorphic to a line. In every day language, this means that a curve is a set of points which, near each of its points, looks like a line, up to a deformation. A simple example of a curve is the parabola, shown to the right. A large number of other curves have been studied in multiple mathematical fields.

The term curve has several meanings in non-mathematical language as well. For example, it can be almost synonymous with mathematical function (as in learning curve), or graph of a function (as in Phillips curve).

An arc or segment of a curve is a part of a curve that is bounded by two distinct end points and contains every point on the curve between its end points. Depending on how the arc is defined, either of the two end points may or may not be part of it. When the arc is straight, it is typically called a line segment.

History

Megalithic art from Newgrange showing an early interest in curves

Fascination with curves began long before they were the subject of mathematical study. This can be seen in numerous examples of their decorative use in art and on everyday objects dating back to prehistoric times.^[2] Curves, or at least their graphical representations, are simple to create, for example by a stick in the sand on a beach.

Historically, the term "line" was used in place of the more modern term "curve". Hence the phrases "straight line" and "right line" were used to distinguish what are today called lines from "curved lines". For example, in Book I of Euclid's Elements, a line is defined as a "breadthless length" (Def. 2), while a straight line is defined as "a line that lies evenly with the points on itself" (Def. 4). Euclid's idea of a line is perhaps clarified by the statement "The extremities of a line are points," (Def. 3).^[3] Later commentators further classified lines according to various schemes. For example:^[4]

• Composite lines (lines forming an angle)
• Incomposite lines
  • Determinate (lines that do not extend indefinitely, such as the circle)
  • Indeterminate (lines that extend indefinitely, such as the straight line and the parabola)

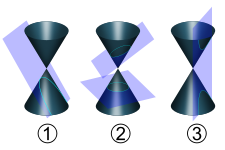The curves created by slicing a cone (conic sections) were among the curves studied in ancient Greece.

The Greek geometers had studied many other kinds of curves. One reason was their interest in solving geometrical problems that could not be solved using standard compass and straightedge construction. These curves include:

• The conic sections, deeply studied by Apollonius of Perga
• The cissoid of Diocles, studied by Diocles and use a method to double the cube.^[5]
• The conchoid of Nicomedes, studied by Nicomedes as a method to both double the cube and to trisect an angle.^[6]
• The Archimedean spiral, studied by Archimedes as a method to trisect an angle and square the circle.^[7]
• The spiric sections, sections of tori studied by Perseus as sections of cones had been studied by Apollonius.

Analytic geometry allowed curves, such as the Folium of Descartes, to be defined using equations instead of geometrical construction.

A fundamental advance in theory of curves was the advent of analytic geometry in the seventeenth century. This enabled a curve to be described using an equation rather than an elaborate geometrical construction. This not only allowed new curves to be defined and studied, but it enabled a formal distinction to be made between curves that can be defined using algebraic equations, algebraic curves, and those that cannot, transcendental curves. Previously, curves had been described as "geometrical" or "mechanical" according to how they were, or supposedly could be, generated.^[2]

Conic sections were applied in astronomy by Kepler. Newton also worked on an early example in the calculus of variations. Solutions to variational problems, such as the brachistochrone and tautochrone questions, introduced properties of curves in new ways (in this case, the cycloid). The catenary gets its name as the solution to the problem of a hanging chain, the sort of question that became routinely accessible by means of differential calculus.

In the eighteenth century came the beginnings of the theory of plane algebraic curves, in general. Newton had studied the cubic curves, in the general description of the real points into 'ovals'. The statement of Bézout's theorem showed a number of aspects which were not directly accessible to the geometry of the time, to do with singular points and complex solutions.

From the nineteenth century there is not a separate curve theory, but rather the appearance of curves as the one-dimensional aspect of projective geometry, and differential geometry; and later topology, when for example the Jordan curve theorem was understood to lie quite deep, as well as being required in complex analysis. The era of the space-filling curves finally provoked the modern definitions of curve.

Topology

Boundaries of hyperbolic components of Mandelbrot set as closed curves

In topology, a curve is defined as follows. Let I be an interval of real numbers (i.e. a non-empty connected subset of $\mathbb{R}$). Then a curve $\!\,\gamma$ is a continuous mapping $\,\!\gamma : I \rightarrow X$, where X is a topological space.

• The curve $\!\,\gamma$ is said to be simple, or a Jordan arc, if it is injective, i.e. if for all x, y in I, we have $\,\!\gamma(x) = \gamma(y) \implies x = y$. If I is a closed bounded interval $\,\![a, b]$, we also allow the possibility $\,\!\gamma(a) = \gamma(b)$ (this convention makes it possible to talk about "closed" simple curves, see below).

In other words this curve "does not cross itself and has no missing points".^[8]

• If γ(x) = γ(y) for some $x\ne y$ (other than the extremities of I), then γ(x) is called a double (or multiple) point of the curve.

• A curve $\!\,\gamma$ is said to be closed or a loop if $\,\!I = [a, b]$ and if $\!\,\gamma(a) = \gamma(b)$. A closed curve is thus a continuous mapping of the circle S¹; a simple closed curve is also called a Jordan curve. The Jordan curve theorem states that such curves divide the plane into an "interior" and an "exterior".

A plane curve is a curve for which X is the Euclidean plane—these are the examples first encountered—or in some cases the projective plane. A space curve is a curve for which X is of three dimensions, usually Euclidean space; a skew curve is a space curve which lies in no plane. These definitions also apply to algebraic curves (see below). However, in the case of algebraic curves it is very common not to restrict the curve to having points only defined over the real numbers.

This definition of curve captures our intuitive notion of a curve as a connected, continuous geometric figure that is "like" a line, without thickness and drawn without interruption, although it also includes figures that can hardly be called curves in common usage. For example, the image of a curve can cover a square in the plane (space-filling curve). The image of simple plane curve can have Hausdorff dimension bigger than one (see Koch snowflake) and even positive Lebesgue measure^[9] (the last example can be obtained by small variation of the Peano curve construction). The dragon curve is another unusual example.

Conventions and terminology

The distinction between a curve and its image is important. Two distinct curves may have the same image. For example, a line segment can be traced out at different speeds, or a circle can be traversed a different number of times. Many times, however, we are just interested in the image of the curve. It is important to pay attention to context and convention in reading.

Terminology is also not uniform. Often, topologists use the term "path" for what we are calling a curve, and "curve" for what we are calling the image of a curve. The term "curve" is more common in vector calculus and differential geometry.

Lengths of curves

Main article: Arc length

If X is a metric space with metric d, then we can define the length of a curve $\!\,\gamma : [a, b] \rightarrow X$ by

$\text{length} (\gamma)=\sup \left\{ \sum_{i=1}^n d(\gamma(t_i),\gamma(t_{i-1})) : n \in \mathbb{N} \text{ and } a = t_0 < t_1 < \cdots < t_n = b \right\}.$

where the sup is over all n and all partitions $t_0 < t_1 < \cdots < t_n$ of [a,b].

A rectifiable curve is a curve with finite length. A parametrization of $\!\,\gamma$ is called natural (or unit speed or parametrised by arc length) if for any t₁, t₂ in [a,b], we have

$\text{length} (\gamma|_{[t_1,t_2]})=|t_2-t_1|.$

If $\!\,\gamma$ is a Lipschitz-continuous function, then it is automatically rectifiable. Moreover, in this case, one can define the speed (or metric derivative) of $\!\,\gamma$ at t₀ as

$\text{speed}(t_0)=\limsup_{t\to t_0} {d(\gamma(t),\gamma(t_0))\over |t-t_0|}$

and then

$\text{length}(\gamma)=\int_a^b \text{speed}(t) \, dt.$

In particular, if $X = \mathbb{R}^n$ is an Euclidean space and $\gamma : [a, b] \rightarrow \mathbb{R}^n$ is differentiable then

$\text{length}(\gamma)=\int_a^b \| \gamma '(t) \| \, dt.$

Differential geometry

Main article: Differential geometry of curves

While the first examples of curves that are met are mostly plane curves (that is, in everyday words, curved lines in two-dimensional space), there are obvious examples such as the helix which exist naturally in three dimensions. The needs of geometry, and also for example classical mechanics are to have a notion of curve in space of any number of dimensions. In general relativity, a world line is a curve in spacetime.

If X is a differentiable manifold, then we can define the notion of differentiable curve in X. This general idea is enough to cover many of the applications of curves in mathematics. From a local point of view one can take X to be Euclidean space. On the other hand it is useful to be more general, in that (for example) it is possible to define the tangent vectors to X by means of this notion of curve.

If X is a smooth manifold, a smooth curve in X is a smooth map

$\!\,\gamma : I \rightarrow X.$

This is a basic notion. There are less and more restricted ideas, too. If X is a C^k manifold (i.e., a manifold whose charts are k times continuously differentiable), then a C^k curve in X is such a curve which is only assumed to be C^k (i.e. k times continuously differentiable). If X is an analytic manifold (i.e. infinitely differentiable and charts are expressible as power series), and γ is an analytic map, then γ is said to be an analytic curve.

A differentiable curve is said to be regular if its derivative never vanishes. (In words, a regular curve never slows to a stop or backtracks on itself.) Two C^k differentiable curves

$\!\,\gamma_1 :I \rightarrow X$ and

$\!\,\gamma_2 : J \rightarrow X$

are said to be equivalent if there is a bijective C^k map

$\!\,p : J \rightarrow I$

such that the inverse map

$\!\,p^{-1} : I \rightarrow J$

is also C^k, and

$\!\,\gamma_{2}(t) = \gamma_{1}(p(t))$

for all t. The map γ₂ is called a reparametrisation of γ₁; and this makes an equivalence relation on the set of all C^k differentiable curves in X. A C^k arc is an equivalence class of C^k curves under the relation of reparametrisation.

Algebraic curve

Main article: Algebraic curve

Algebraic curves are the curves considered in algebraic geometry. A plane algebraic curve is the locus of points f(x, y) = 0, where f(x, y) is a polynomial in two variables defined over some field F. Algebraic geometry normally looks at such curves in the context of algebraically closed fields. If K is the algebraic closure of F, and C is a curve defined by a polynomial f(x, y) defined over F, the points of the curve defined over F, consisting of pairs (a, b) with a and b in F, can be denoted C(F); the full curve itself being C(K).

Algebraic curves can also be space curves, or curves in even higher dimensions, obtained as the intersection (common solution set) of more than one polynomial equation in more than two variables. By eliminating variables by means of the resultant, these can be reduced to plane algebraic curves, which however may introduce singularities such as cusps or double points. We may also consider these curves to have points defined in the projective plane; if f(x, y) = 0 then if x = u/w and y = v/w, and n is the total degree of f, then by expanding out wⁿf(u/w, v/w) = 0 we obtain g(u, v, w) = 0, where g is homogeneous of degree n. An example is the Fermat curve uⁿ + vⁿ = wⁿ, which has an affine form xⁿ + yⁿ = 1.

Important examples of algebraic curves are the conics, which are nonsingular curves of degree two and genus zero, and elliptic curves, which are nonsingular curves of genus one studied in number theory and which have important applications to cryptography. Because algebraic curves in fields of characteristic zero are most often studied over the complex numbers, algbebraic curves in algebraic geometry look like real surfaces. Looking at them projectively, if we have a nonsingular curve in n dimensions, we obtain a picture in the complex projective space of dimension n, which corresponds to a real manifold of dimension 2n, in which the curve is an embedded smooth and compact surface with a certain number of holes in it, the genus. In fact, non-singular complex projective algebraic curves are compact Riemann surfaces.

See also

Curvature Curve orientation Curves in differential geometry Curve sketching Differential geometry of curves French curve Gallery of curves

List of curves List of curve topics Osculating circle Parametric surface Path (topology) Position vector Vector-valued function

Notes

1. ^ In current language, a line is typically required to be straight. Historically, however, lines could be "curved" or "straight".
2. ^ ^{a b} Lockwood p. ix
3. ^ Heath p. 153
4. ^ Heath p. 160
5. ^ Lockwood p. 132
6. ^ Lockwood p. 129
7. ^ O'Connor, John J.; Robertson, Edmund F., "Spiral of Archimedes", MacTutor History of Mathematics archive, University of St Andrews, http://www-history.mcs.st-andrews.ac.uk/Curves/Spiral.html .
8. ^ Jordan arc definition at Dictionary.com. Dictionary.com Unabridged. Random House, Inc.
9. ^ Osgood, William F. (January 1903). "A Jordan Curve of Positive Area". Transactions of the American Mathematical Society (American Mathematical Society) 4 (1): 107–112. doi:10.2307/1986455. ISSN 0002-9947. JSTOR 1986455. 

References

• A.S. Parkhomenko (2001), "Line (curve)", in Hazewinkel, Michiel, Encyclopaedia of Mathematics, Springer, ISBN 978-1556080104, http://eom.springer.de/l/l059020.htm 
• B.I. Golubov (2001), "Rectifiable curve", in Hazewinkel, Michiel, Encyclopaedia of Mathematics, Springer, ISBN 978-1556080104, http://eom.springer.de/r/r080130.htm 
• Euclid, commentary and trans. by T. L. Heath Elements Vol. 1 (1908 Cambridge) Google Books
• E. H. Lockwood A Book of Curves (1961 Cambridge)

External links

• Famous Curves Index, School of Mathematics and Statistics, University of St Andrews, Scotland
• Mathematical curves A collection of 874 two-dimensional mathematical curves
• [1] Gallery of Space Curves Made from Circles, includes animations by Peter Moses
• [2] Gallery of Bishop Curves and Other Sperical Curves, includes animations by Peter Moses
• YAN Kun. Research on adaptive connection equation in discontinuous area of data curve. DOI:10.3969/j.issn.1004-2903.2011.01.018