Parabola

For other uses, see Parabola (disambiguation).

A parabola

A parabola obtained as the intersection of a cone with a plane parallel to a straight line on its surface.

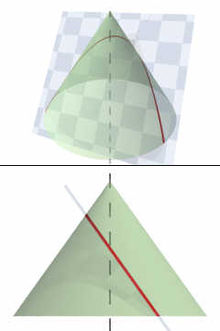
In mathematics, the parabola ( /pəˈræbələ/; plural parabolae or parabolas, from the Greek παραβολή) is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface. Given a point (the focus) and a corresponding line (the directrix) on the plane, the locus of points in that plane that are equidistant from them is a parabola.

The line perpendicular to the directrix and passing through the focus (that is, the line that splits the parabola through the middle) is called the "axis of symmetry". The point on the axis of symmetry that intersects the parabola is called the "vertex", and it is the point where the curvature is greatest. Parabolas can open up, down, left, right, or in some other arbitrary direction. Any parabola can be repositioned and rescaled to fit exactly on any other parabola — that is, all parabolas are similar.

The parabola has many important applications, from automobile headlight reflectors to the design of ballistic missiles. They are frequently used in physics, engineering, and many other areas.

History

Parabolic compass designed by Leonardo da Vinci

Parabolae are conic sections

The earliest known work on conic sections was by Menaechmus in the fourth century BC. He discovered a way to solve the problem of doubling the cube using parabolae. (The solution, however, does not meet the requirements imposed by compass and straightedge construction.) The area enclosed by a parabola and a line segment, the so-called "parabola segment", was computed by Archimedes via the method of exhaustion in the third century BC, in his The Quadrature of the Parabola. The name "parabola" is due to Apollonius, who discovered many properties of conic sections. The focus–directrix property of the parabola and other conics is due to Pappus.

Galileo showed that the path of a projectile follows a parabola, a consequence of uniform acceleration due to gravity.

The idea that a parabolic reflector could produce an image was already well known before the invention of the reflecting telescope.^[1] Designs were proposed in the early to mid seventeenth century by many mathematicians including René Descartes, Marin Mersenne,^[2] and James Gregory.^[3] When Isaac Newton built the first reflecting telescope in 1668 he skipped using a parabolic mirror because of the difficulty of fabrication, opting for a spherical mirror. Parabolic mirrors are used in most modern reflecting telescopes and in satellite dishes and radar receivers.^[4]

Equation in Cartesian coordinates

Let the directrix be the line x = −p and let the focus be the point (p, 0). If (x, y) is a point on the parabola then, by Pappus' definition of a parabola, it is the same distance from the directrix as the focus; in other words:

$x+p=\sqrt{(x-p)^2+y^2}$

Squaring both sides and simplifying produces

$y^2 = 4px\$

as the equation of the parabola. By interchanging the roles of x and y one obtains the corresponding equation of a parabola with a vertical axis as

$x^2 = 4py\$

The equation can be generalized to allow the vertex to be at a point other than the origin by defining the vertex as the point (h, k). The equation of a parabola with a vertical axis then becomes

$(x-h)^{2}=4p(y-k)\,$

The last equation can be rewritten

$y=ax^2+bx+c\,$

so the graph of any function which is a polynomial of degree 2 in x is a parabola with a vertical axis.

More generally, a parabola is a curve in the Cartesian plane defined by an irreducible equation — one that does not factor as a product of two not necessarily distinct linear equations — of the general conic form

$A x^{2} + B xy + C y^{2} + D x + E y + F = 0 \,$

with the parabola restriction that

$B^{2} = 4 AC,\,$

where all of the coefficients are real and where A and C are not both zero. The equation is irreducible if and only if the determinant of the 3×3 matrix

$\begin{bmatrix} A & B/2 & D/2 \\ B/2 & C & E/2 \\ D/2 & E/2 & F \end{bmatrix}.$

is non-zero: that is, if (AC - B²/4)F + BED/4 - CD²/4 - AE²/4 ≠ 0. The reducible case, also called the degenerate case, gives a pair of parallel lines, possibly real, possibly imaginary, and possibly coinciding with each other.^[5]

Other geometric definitions

A parabola may also be characterized as a conic section with an eccentricity of 1. As a consequence of this, all parabolae are similar, meaning that while they can be different sizes, they are all the same shape. A parabola can also be obtained as the limit of a sequence of ellipses where one focus is kept fixed as the other is allowed to move arbitrarily far away in one direction. In this sense, a parabola may be considered an ellipse that has one focus at infinity. The parabola is an inverse transform of a cardioid.

A parabola has a single axis of reflective symmetry, which passes through its focus and is perpendicular to its directrix. The point of intersection of this axis and the parabola is called the vertex. A parabola spun about this axis in three dimensions traces out a shape known as a paraboloid of revolution.

The parabola is found in numerous situations in the physical world (see below).

Equations

Cartesian

Vertical axis of symmetry

$(x - h)^2 = 4p(y - k) \,$

$y =\frac{(x-h)^2}{4p}+k\,$

$y = ax^2 + bx + c \,$

where

$a = \frac{1}{4p}; \ \ b = \frac{-h}{2p}; \ \ c = \frac{h^2}{4p} + k; \ \$

$h = \frac{-b}{2a}; \ \ k = \frac{4ac - b^2}{4a}$.

Parametric form:

$x(t) = 2pt + h; \ \ y(t) = pt^2 + k \,$

Horizontal axis of symmetry

$(y - k)^2 = 4p(x - h) \,$

$x =\frac{(y - k)^2}{4p} + h;\ \,$

$x = ay^2 + by + c \,$

where

$a = \frac{1}{4p}; \ \ b = \frac{-k}{2p}; \ \ c = \frac{k^2}{4p} + h; \ \$

$h = \frac{4ac - b^2}{4a}; \ \ k = \frac{-b}{2a}$.

Parametric form:

$x(t) = pt^2 + h; \ \ y(t) = 2pt + k \,$

General parabola

The general form for a parabola is

$(\alpha x+\beta y)^2 + \gamma x + \delta y + \epsilon = 0 \,$

This result is derived from the general conic equation given below:

$Ax^2 +Bxy + Cy^2 + Dx + Ey + F = 0 \,$

and the fact that, for a parabola,

$B^2=4AC \,$.

The equation for a general parabola with a focus point F(u, v), and a directrix in the form

$ax+by+c=0 \,$

is

$\frac{\left(ax+by+c\right)^2}{{a}^{2}+{b}^{2}}=\left(x-u\right)^2+\left(y-v\right)^2 \,$

Latus rectum, semi-latus rectum, and polar coordinates

In polar coordinates, a parabola with the focus at the origin and the directrix parallel to the y-axis, is given by the equation

$r (1 + \cos \theta) = l \,$

where l is the semilatus rectum: the distance from the focus to the parabola itself, measured along a line perpendicular to the axis. Note that this is twice the distance from the focus to the vertex of the parabola or the perpendicular distance from the focus to the latus rectum.

The latus rectum is the chord that passes through the focus and is perpendicular to the axis. It has a length of 2l.

Gauss-mapped form

A Gauss-mapped form: (tan ²ϕ,2tan ϕ) has normal (cos ϕ,sin ϕ).

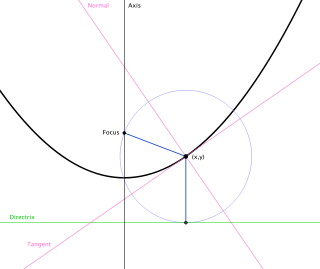
Derivation of the focus

Parabolic curve showing directrix (L) and focus (F). The distance from a given point P_n to the focus is always the same as the distance from P_n to a point Q_n directly below, on the directrix.

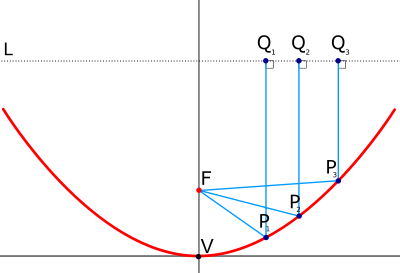Parabolic curve showing arbitrary line (L), focus (F), and vertex (V). L is an arbitrary line perpendicular to the axis of symmetry and opposite the focus of the parabola from the vertex (i.e. farther from V than from F.) The length of any line F - P_n - Q_n is the same. This is similar to saying that a parabola is an ellipse, but with one focal point at infinity.

To derive the focus of a simple parabola, where the axis of symmetry is parallel to the y-axis with the vertex at (0,0), such as

$y = a x^2\,\!$

then there is a point (0,f)—the focus, F—such that any point P on the parabola will be equidistant from both the focus and the linear directrix, L. The linear directrix is a line perpendicular to the axis of symmetry of the parabola (in this case parallel to the x axis) and passes through the point (0,-f). So any point P=(x,y) on the parabola will be equidistant both to (0,f) and (x,-f).

FP, a line from the focus to a point on the parabola, has the same length as QP, a line drawn from that point on the parabola perpendicular to the linear directrix, intersecting at point Q.

Imagine a right triangle with two legs, x and f-y (the vertical distance between F and P). The length of the hypotenuse, FP, is given by

$\| FP \| = \sqrt{ x^2 + (f - y)^2 }\,\!$

(Note that (f-y) and (y-f) produce the same result because it is squared.)

The line QP is given by adding y (the vertical distance between the point P and the x-axis) and f (the vertical distance between the x-axis and the linear directrix).

$\| QP \| = f + y\,\!$

These two line segments are equal, and, as indicated above, y=ax², thus

$\| FP \| = \| QP \| \,\!$

$\sqrt{x^2 + (f - a x^2 )^2 } = f + a x^2\,\!$

Square both sides,

$x^2 + (f^2 - 2 a x^2 f + a^2 x^4) = (f^2 + 2 a x^2 f + a^2 x^4)\,\!$

Cancel out terms from both sides,

$x^2 - 2 a x^2 f = 2 a x^2 f\,\!$

$x^2 = 4 a x^2 f\,\!$

Divide out the x² from both sides (we assume that x is not zero),

$1 = 4 a f\,\!$

$f = {1 \over 4 a }\,\!$

So, for a parabola such as f(x)=x², the a coefficient is 1, so the focus F is (0,¼)

As stated above, this is the derivation of the focus for a simple parabola, one centered at the origin and with symmetry around the y-axis. For any generalized parabola, with its equation given in the standard form

$y=ax^2+bx+c\,\!$,

the focus is located at the point

$\left (\frac{-b}{2a},\frac{-b^2}{4a}+c+\frac{1}{4a} \right)\,\!$

which may also be written as

$\left (\frac{-b}{2a},c-\frac{b^2-1}{4a} \right)\,\!$

and the directrix is designated by the equation

$y=\frac{-b^2}{4a}+c-\frac{1}{4a}\,\!$

which may also be written as

$y=c-\frac{b^2+1}{4a}\,\!$

Reflective property of the tangent

A diagram showing the reflective property, the directrix (solid green), and the lines connecting the focus and directrix to the parabola (blue)

The tangent of the parabola described by equation y=ax² has slope

${dy \over dx} = 2 a x = {2 y \over x}$

This line intersects the y-axis at the point (0,-y) = (0, - a x²), and the x-axis at the point (x/2,0). Let this point be called G. Point G is also the midpoint of line segment FQ:

$F = (0,f), \quad$

$Q = (x,-f), \quad$

${F + Q \over 2} = {(0,f) + (x,-f) \over 2} = {(x,0) \over 2} = \left({x \over 2}, 0\right).$

Since G is the midpoint of line FQ, this means that

$\| FG \| \cong \| GQ \|,$

and it is already known that P is equidistant from both F and Q:

$\| PF \| \cong \| PQ \|,$

and, thirdly, line GP is equal to itself, therefore:

$\Delta FGP \cong \Delta QGP$

It follows that $\angle FPG \cong \angle GPQ$.

Line QP can be extended beyond P to some point T, and line GP can be extended beyond P to some point R. Then $\angle RPT$ and $\angle GPQ$ are vertical, so they are equal (congruent). But $\angle GPQ$ is equal to $\angle FPG$. Therefore $\angle RPT$ is equal to $\angle FPG$.

The line RG is tangent to the parabola at P, so any light beam bouncing off point P will behave as if line RG were a mirror and it were bouncing off that mirror.

Let a light beam travel down the vertical line TP and bounce off from P. The beam's angle of inclination from the mirror is $\angle RPT$, so when it bounces off, its angle of inclination must be equal to $\angle RPT$. But $\angle FPG$ has been shown to be equal to $\angle RPT$. Therefore the beam bounces off along the line FP: directly towards the focus.

Conclusion: Any light beam moving vertically downwards in the concavity of the parabola (parallel to the axis of symmetry) will bounce off the parabola moving directly towards the focus. (See parabolic reflector.)

The same reasoning can be applied to a parabola whose axis is vertical, so that it can be specified by the equation

$y = ax^2 + bx + c \,$.

The tangent has then a generic slope of

$m_{tan} = 2ax + b \,$.

Reflection derivation, together with trigonometric angle addition rules, leads to the result that the reflected ray has a slope of

$m_{ref} = {m_{tan}^2 - 1 \over 2m_{tan}}$.

Another tangent property

Let the line of symmetry intersect the parabola at point Q, and denote the focus as point F and its distance from point Q as f. Let the perpendicular to the line of symmetry, through the focus, intersect the parabola at a point T. Then (1) the distance from F to T is 2f, and (2) a tangent to the parabola at point T intersects the line of symmetry at a 45° angle.^[6]:p.26

When b varies

The x-coordinate at the vertex is $x=-\frac{b}{2a}$, which is found by deriving the original equation y = ax² + bx + c, setting the resulting dy / dx = 2ax + b equal to zero (a critical point), and solving for x. Substitute this x-coordinate into the original equation to yield:

$y=a\left (-\frac{b}{2a}\right )^2 + b \left ( -\frac{b}{2a} \right ) + c$

Simplifying:

$=\frac{ab^2}{4a^2} -\frac{b^2}{2a} + c$

$=\frac{b^2}{4a} -\frac{2\cdot b^2}{2\cdot 2a} + c\cdot\frac{4a}{4a}$

$=\frac{-b^2+4ac}{4a}$

$=-\frac{b^2-4ac}{4a}=-\frac{D}{4a}$

Thus, the vertex is at point

$\left (-\frac{b}{2a},-\frac{D}{4a}\right )$

Parabolae in the physical world

A bouncing ball captured with a stroboscopic flash at 25 images per second. Note that the ball becomes significantly non-spherical after each bounce, especially after the first. That, along with spin and air resistance, causes the curve swept out to deviate slightly from the expected perfect parabola.

Parabolic trajectories of water in a fountain.

In nature, approximations of parabolae and paraboloids (such as catenary curves) are found in many diverse situations. The best-known instance of the parabola in the history of physics is the trajectory of a particle or body in motion under the influence of a uniform gravitational field without air resistance (for instance, a baseball flying through the air, neglecting air friction).

The parabolic trajectory of projectiles was discovered experimentally by Galileo in the early 17th century, who performed experiments with balls rolling on inclined planes. He also later proved this mathematically in his book Dialogue Concerning Two New Sciences.^[7][8] For objects extended in space, such as a diver jumping from a diving board, the object itself follows a complex motion as it rotates, but the center of mass of the object nevertheless forms a parabola. As in all cases in the physical world, the trajectory is always an approximation of a parabola. The presence of air resistance, for example, always distorts the shape, although at low speeds, the shape is a good approximation of a parabola. At higher speeds, such as in ballistics, the shape is highly distorted and does not resemble a parabola.

Another situation in which parabolae may arise in nature is in two-body orbits, for example, of a small planetoid or other object under the influence of the gravitation of the sun. Such parabolic orbits are a special case that are rarely found in nature. Orbits that form a hyperbola or an ellipse are much more common. In fact, the parabolic orbit is the borderline case between those two types of orbit. An object following a parabolic orbit moves at the exact escape velocity of the object it is orbiting, while elliptical orbits are slower and hyperbolic orbits are faster.

Hercilio Luz Bridge, Florianópolis, Brazil. Suspension bridges follow a curve which is intermediate between a parabola and a catenary.^[9]

Approximations of parabolae are also found in the shape of the main cables on a simple suspension bridge. The curve of the chains of a suspension bridge is always an intermediate curve between a parabola and a catenary, but in practice the curve is generally nearer to a parabola, and in calculations the second degree parabola is used.^[9][10] Under the influence of a uniform load (such as a horizontal suspended deck), the otherwise hyperbolic cable is deformed toward a parabola. Unlike an inelastic chain, a freely-hanging spring of zero unstressed length takes the shape of a parabola.

Paraboloids arise in several physical situations as well. The best-known instance is the parabolic reflector, which is a mirror or similar reflective device that concentrates light or other forms of electromagnetic radiation to a common focal point. The principle of the parabolic reflector may have been discovered in the 3rd century BC by the geometer Archimedes, who, according to a legend of debatable veracity,^[11] constructed parabolic mirrors to defend Syracuse against the Roman fleet, by concentrating the sun's rays to set fire to the decks of the Roman ships. The principle was applied to telescopes in the 17th century. Today, paraboloid reflectors can be commonly observed throughout much of the world in microwave and satellite dish antennas.

Parabolic shape formed by a liquid surface under rotation. Two liquids of different densities are contained in a narrow rectangular tank.^{[clarification needed]}

Paraboloids are also observed in the surface of a liquid confined to a container and rotated around the central axis. In this case, the centrifugal force causes the liquid to climb the walls of the container, forming a parabolic surface. This is the principle behind the liquid mirror telescope.

Aircraft used to create a weightless state for purposes of experimentation, such as NASA's “Vomit Comet,” follow a vertically parabolic trajectory for brief periods in order to trace the course of an object in free fall, which produces the same effect as zero gravity for most purposes.

Vertical curves in roads are usually parabolic by design.

Generalizations

In algebraic geometry, the parabola is generalized by the rational normal curves, which have coordinates $(x,x^2,x^3,\dots,x^n);$ the standard parabola is the case n = 2, and the case n = 3 is known as the twisted cubic. A further generalization is given by the Veronese variety, when there are more than one input variable.

In the theory of quadratic forms, the parabola is the graph of the quadratic form x² (or other scalings), while the elliptic paraboloid is the graph of the positive-definite quadratic form x² + y² (or scalings) and the hyperbolic paraboloid is the graph of the indefinite quadratic form x² − y². Generalizations to more variables yield further such objects.

The curves y = x^p for other values of p are traditionally referred to as the higher parabolas, and were originally treated implicitly, in the form x^p = ky^q for p and q both positive integers, in which form they are seen to be algebraic curves. These correspond to the explicit formula y = x^{p / q} for a positive fractional power of x. Negative fractional powers correspond to the implicit equation x^py^q = k, and are traditionally referred to as higher hyperbolas. Analytically, x can also be raised to an irrational power (for positive values of x); the analytic properties are analogous to when x is raised to rational powers, but the resulting curve is no longer algebraic, and cannot be analyzed via algebraic geometry.

See also

• Catenary
• Ellipse
• Hyperbola
• Universal parabolic constant
• Parabolic reflector
• Parabolic partial differential equation
• Paraboloid
• Quadratic equation
• Quadratic function

Notes

1. ^ Wilson, Ray N. (2004). Reflecting Telescope Optics: Basic design theory and its historical development (2 ed.). Springer. p. 3. ISBN 3-540-40106-7. http://books.google.com/books?id=PuN7l2A2uzQC. , Extract of page 3
2. ^ Stargazer, p. 115.
3. ^ Stargazer, pp. 123 and 132
4. ^ Fitzpatrick, Richard (July 14, 2007), "Spherical Mirrors", Electromagnetism and Optics, lectures, University of Texas at Austin, Paraxial Optics, http://farside.ph.utexas.edu/teaching/316/lectures/node136.html, retrieved October 5, 2011. 
5. ^ Lawrence, J. Dennis, A Catalog of Special Plane Curves, Dover Publ., 1972.
6. ^ Downs, J. W., Practical Conic Sections, Dover Publ., 2003.
7. ^ Dialogue Concerning Two New Sciences (1638) (The Motion of Projectiles: Theorem 1); see [1]
8. ^ However, this parabolic shape, as Newton recognized, is only an approximation of the actual elliptical shape of the trajectory, and is obtained by assuming that the gravitational force is constant (not pointing toward the center of the earth) in the area of interest. Often, this difference is negligible, and leads to a simpler formula for tracking motion.
9. ^ ^{a b} Troyano, Leonardo Fernández (2003). Bridge engineering: a global perspective. Thomas Telford. p. 536. ISBN 0-727-73215-3. http://books.google.com/books?id=0u5G8E3uPUAC. , Chapter 8 page 536
10. ^ Drewry, Charles Stewart (1832). A memoir of suspension bridges. Oxford University. p. 159. http://books.google.com/books?id=Nk-pQT7-EM4C. , Extract of page 159
11. ^ Middleton, W. E. Knowles (December 1961). "Archimedes, Kircher, Buffon, and the Burning-Mirrors". Isis (Published by: The University of Chicago Press on behalf of The History of Science Society) 52 (4): 533–543. doi:10.1086/349498. http://www.jstor.org/stable/228646. Retrieved October 5, 2011. 

References

• Lockwood, E. H. (1961): A Book of Curves, Cambridge University Press

External links

• Apollonius' Derivation of the Parabola at Convergence
• Weisstein, Eric W., "Parabola" from MathWorld.
• Interactive parabola-drag focus, see axis of symmetry, directrix, standard and vertex forms
• Archimedes Triangle and Squaring of Parabola at cut-the-knot
• Two Tangents to Parabola at cut-the-knot
• Parabola As Envelope of Straight Lines at cut-the-knot
• Parabolic Mirror at cut-the-knot
• Three Parabola Tangents at cut-the-knot
• Module for the Tangent Parabola
• Focal Properties of Parabola at cut-the-knot
• Parabola As Envelope II at cut-the-knot
• The similarity of parabola at Dynamic Geometry Sketches
• a method of drawing a parabola with string and tacks