- Parabolic reflector
-
A parabolic reflector (or dish or mirror) is a reflective device used to collect or project energy such as light, sound, or radio waves. Its shape is that of a circular paraboloid, that is, the surface generated by a parabola revolving around its axis. The parabolic reflector transforms an incoming plane wave traveling along the axis into a spherical wave converging toward the focus. Conversely, a spherical wave generated by a point source placed in the focus is transformed into a plane wave propagating as a collimated beam along the axis.
Parabolic reflectors are used to collect energy from a distant source (for example sound waves or incoming star light) and bring it to a common focal point,[1] thus correcting spherical aberration found in simpler spherical reflectors. Since the principles of reflection are reversible, parabolic reflectors can also be used to project energy of a source at its focus outward in a parallel beam,[2] used in devices such as spotlights and car headlights.
Contents
Theory
 One of the world's largest solar parabolic dishes at the Ben-Gurion National Solar Energy Center in Israel.
One of the world's largest solar parabolic dishes at the Ben-Gurion National Solar Energy Center in Israel.
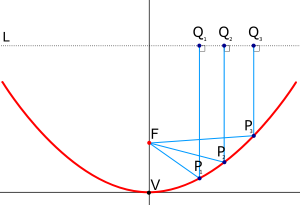
The parabolic reflector functions due to the geometric properties of the paraboloidal shape: if the angle of incidence to the inner surface of the collector equals the angle of reflection, then any incoming ray that is parallel to the axis of the dish will be reflected to a central point, or "focus". Because many types of energy can be reflected in this way, parabolic reflectors can be used to collect and concentrate energy entering the reflector at a particular angle. Similarly, energy radiating from the "focus" to the dish can be transmitted outward in a beam that is parallel to the axis of the dish.
In contrast with spherical reflectors, which suffer from a spherical aberration that becomes stronger as the ratio of the beam diameter to the focal distance becomes larger, the parabolic reflectors can be made to accommodate beams of any width. However, if the incoming beam makes a non-zero angle with the axis (or if the emitting point source is not placed in the focus), parabolic reflectors suffer from an aberration called coma. This is primarily of interest in telescopes because most other applications do not require sharp resolution off the axis of the parabola.
History
The principle of parabolic reflectors has been known since classical antiquity, when the mathematician Diocles described them in his book On Burning Mirrors and proved that they focus a parallel beam to a point.[3] Archimedes in the third century BC studied paraboloids as part of his study of hydrostatic equilibrium,[4] and it has been claimed that he used reflectors to set the Roman fleet alight during the Siege of Syracuse.[5] This seems unlikely to be true, however, as the claim does not appear in sources before the 2nd century AD, and Diocles does not mention it in his book.[6] Parabolic mirrors were also studied by the physicist Ibn Sahl in the 10th century.[7] James Gregory, in his 1663 book Optica Promota (1663), pointed out that a reflecting telescope with a mirror that was parabolic would correct spherical aberration as well as the chromatic aberration seen in refracting telescopes. The design he came up with bears his name: the "Gregorian telescope"; but according to his own confession, Gregory had no practical skill and he could find no optician capable of actually constructing one.[8] Isaac Newton knew about the properties of parabolic mirrors but chose a spherical shape for his Newtonian telescope mirror to simplify construction.[9] Lighthouses also commonly used parabolic mirrors to collimate a point of light from a lantern into a beam, before being replaced by more efficient fresnel lenses in the 19th century.
Applications
The most common modern applications of the parabolic reflector are in satellite dishes, reflecting telescopes, radio telescopes, parabolic microphones, and many lighting devices such as spotlights, car headlights, PAR cans and LED housings.[10]
The Olympic Flame has been lit using a parabolic reflector concentrating sunlight. Parabolic mirrors are one of many shapes for a burning-glass.
A parabolic reflector pointing upward can be formed by rotating a reflective liquid, like mercury, around a vertical axis. This makes the liquid mirror telescope possible.
A mirascope, mirage bowl, or parabolic mirror wok is a toy consisting of two parabolic mirrors that are put together like a wok pan and a lid with a hole in it. The device produces an upright real image (with the magnification 1) of an object placed on the bottom of it, which gives the optical illusion that something is in the hole of the lid (while actually it is at the bottom of the pan below).
Parabolic reflectors are a popular alternative for increasing wireless signal strength. Even with simple ones, users have reported 3 dB or more gains.[11][12]
See also
- Parabola
- Parabolic antenna
- Parabolic trough
- Paraboloid
- Spherical reflector
- Toroidal reflector
- Solar furnace
References
- ^ telescopemaking.org The Basics of Telescope Testing - Mathematical Details "A spherical mirror takes light rays which emanate from a single point (called the center of curvature and send them back exactly to that point. If stars were that close, a spherical mirror would be ideal, but real stars are a good deal further away, in fact, for all practical purposes, stars are located at an infinite distance."
- ^ farside.ph.utexas.edu - Spherical Mirrors, by Richard Fitzpatrick 2007-07-14 "Since the path of a light-ray is completely reversible, it follows that a light source placed at the focus $F$ of a parabolic mirror yields a perfectly parallel beam of light, after the light has reflected off the surface of the mirror."
- ^ pp. 162–164, Apollonius of Perga's Conica: text, context, subtext, Michael N. Fried and Sabetai Unguru, Brill, 2001, ISBN 9004119779.
- ^ pp. 73–74, The forgotten revolution: how science was born in 300 BC and why it had to be reborn, Lucio Russo, Birkhäuser, 2004, ISBN 3540200681.
- ^ "Archimedes' Weapon". Time Magazine. November 26, 1973. http://www.time.com/time/magazine/article/0,9171,908175,00.html?promoid=googlep. Retrieved 2007-08-12.
- ^ p. 72, The Geometry of Burning-Mirrors in Antiquity, Wilbur Knorr, Isis 74 #1 (March 1983), pp. 53–73, doi:10.1086/353176.
- ^ pp. 465, 468, 469, A Pioneer in Anaclastics: Ibn Sahl on Burning Mirrors and Lenses, Roshdi Rashed, Isis, 81, #3 (September 1990), pp. 464–491, doi:10.1086/355456.
- ^ A Biographical Dictionary of Eminent Scotsmen By Robert Chambers, Thomas - Page 175
- ^ Electronic Imaging in Astronomy By Ian S. McLean - Page 77
- ^ farside.ph.utexas.edu - Spherical Mirrors, by Richard Fitzpatrick 2007-07-14
- ^ binarywolf.com - DIY Wireless Antenna
- ^ http://www.wired.com/culture/lifestyle/multimedia/2004/08/64440?slide=2&slideView=2 wired.com - wifi shootout 2005
External links
- Java demonstration of a parabolic reflector
- Algorithm and spreadsheet for making a simple paraboloid: Design and make a paraboloid for use as a solar concentrator, sound mirror or microwave antenna.
- JavaScript calculator and algorithm for designing paraboloids: Design and make a paraboloid approximated by flat surface segments.
- Parabolic Reflector Antennas www.antenna-theory.com
Software
- Parabola Calculator version 2.0 Freeware program written to help design solar collector or wifi projects using parabolic reflectors.
Categories:- Mirrors
Wikimedia Foundation. 2010.