Cissoid of Diocles

Cissoid of Diocles construction

In geometry, the cissoid of Diocles is a cubic plane curve notable for the property that it can be used to construct two mean proportionals to a given ratio. In particular, it can be used to double a cube. It can be defined as the cissoid of a circle and a line tangent to it with respect to the point on the circle opposite to the point of tangency. In fact, the family of cissoids is named for this example and some authors refer to it simply as the cissoid. It has a single cusp at the pole, and is symmetric about the diameter of the circle which is the line of tangency of the cusp. The line is an asymptote. It is a member of the conchoid of de Sluze family of curves and in form it resembles a tractrix.

The word "cissoid" comes from the Greek κισσοείδες kissoeidēs "ivy shaped" from κισσός kissos "ivy" and -οειδές -oeidēs "having the likeness of". The curve is named for Diocles who studied it in the 2nd century BCE.

Construction and equations

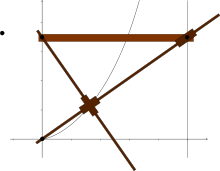
Let C be a circle with diameter OA and let L be the line tangent to the circle at A. Draw a variable ray R through O to intersect C at M₁ and L at M₂. Let M be the point on R so that OM = M₁M₂. The cissoid is then defined to be the locus of points M.

Let the radius of C be a. By translation and rotation, we may take O to be the origin and the center of the circle to be (a, 0), so A is (2a, 0). Then the polar equations of L and C are:

r = 2asec θ

r = 2acos θ.

By construction, the distance from the origin to a point on the cissoid is equal the difference between the distances between the origin and the corresponding points on L and C. In other words, the polar equation of the cissoid is

r = 2asec θ − 2acos θ = 2a(sec θ − cos θ).

Applying some trigonometric identities, this is equivalent to

r = 2asin ²θ / cos θ = 2asin θtan θ.

Let t = tan θ in the above equation. Then

$x = r\cos\theta = 2a\sin^2\theta = \frac{2a\tan^2\theta}{\sec^2\theta} = \frac{2at^2}{1+t^2}$

$y = tx = \frac{2at^3}{1+t^2}$

are parametric equations for the cissoid.

Converting the polar form to Cartesian coordinates produces

(x² + y²)x = 2ay²

Construction by double projection

Mechanism to generate the cissoid

Another construction proceeds as follows: Let a line L and a point O not on L be given, and let K be the line through O parallel to L. Let P be a variable point on L. Let Q be the projection of P onto K, on other words Q is the intersection of K with the line through P perpendicular to K. Similarly let R be the projection of Q onto OP. Then the cissoid is the locus of points R.

To see this, let O be the origin and L the line x=2a as above. Let P be the point (2a, 2at), then Q is (0, 2at) and the equation of the line OP is y=tx. The line through Q perpendicular to OP is

t(y − 2at) + x = 0.

To find the point of intersection R, set y=tx in this equation to get

$t(tx-2a)+x=0,\ x(t^2+1)=2at^2,\ x=\frac{2at^2}{t^2+1}$

$y=tx=\frac{2at^3}{t^2+1}$

which are the parametric equations given above.

This construction suggests the mechanism shown to the right as a way to generate the curve.

Newton's construction

Newton's construction

The following construction was given by Isaac Newton. Let J be a line and B a point not on J. Let BST be a right angle which moves so that ST equals the distance from B to J and T remains on J, while the other leg BS slides along B. Then the midpoint P of ST describes the curve.

To see this,^[1] let the distance between B and J be 2a. By translation and rotation, take B = (−a, 0) and J the line x=a. Let P = (x, y) and let ψ be the angle between SB and the x-axis; this is equal to the angle between ST and J. By construction, PT = a, so the distance from P to J is a sin ψ. In other words a-x = a sin ψ. Also, SP = a is the y coordinate of (x, y) if it is rotated by angle ψ, so a = (x+a) sin ψ + y cos ψ. After simplification, this produces parametric equations

$x=a(1-\sin\psi),\,y=a\frac{(1-\sin\psi)^2}{\cos\psi}.$

Change parameters by replacing ψ with its compliment to get

$x=a(1-\cos\psi),\,y=a\frac{(1-\cos\psi)^2}{\sin\psi}$

or, applying double angle formulas,

$x=2a\sin^2{\psi \over 2},\,y=a\frac{4\sin^4{\psi \over 2}}{2\sin{\psi \over 2}\cos{\psi \over 2}} = 2a\frac{\sin^3{\psi \over 2}}{\cos{\psi \over 2}}.$

But this is polar equation

r = 2asin ²θ / cos θ

given above with θ=Ψ/2.

Note that, as with the double projection construction, this can be adapted to produce a mechanical device that generates the curve.

Delian problem

The Greek geometer Diocles used the cissoid to obtain two mean proportionals to a given ratio. This means that given lengths a and b, the curve can be used to find u and v so that u/a=v/u=b/v. As a special case, this can be used to solve the Delian problem: how much must the length of a cube be increased in order to double its volume? Specifically, if a is the side of a cube, and b=2a, then the volume of a cube of side u is

$u^3=a^3(\tfrac{u}{a})^3=a^3(\tfrac{u}{a})(\tfrac{v}{u})(\tfrac{b}{v})=a^3(\tfrac{b}{a})=2a^3$

so u is the side of a cube with double the volume of the original cube. Note however that this solution does not fall within the rules of compass and straightedge construction since it relies on the existence of the cissoid.

Let a and b be given. It is required to find u so that u³=a²b, giving u and v=u²/a as the mean proportionals. Let the cissoid

(x² + y²)x = 2ay²

be constructed as above, with O the origin, A the point (2a, 0), and J the line x=a, also as given above. Let C be the point of intersection of J with OA. From the given length b, mark B on J so that CB=b. Draw BA and let P = (x, y) be the point where it intersects the cissoid. Draw OP and let it intersect J at U. Then u=CU is the required length.

To see this,^[2] rewrite the equation of the curve as

$y^2=\frac{x^3}{2a-x}$

and let N = (x, 0), so PN is the perpendicular to OA through P. From the equation of the curve,

$PN^2=\frac{ON^3}{NA}.$

From this,

$\frac{PN^3}{ON^3}=\frac{PN}{NA}.$

By similar triangles PN/ON=UA/OA and PM/MA=BO/OA. So the equation becomes

$\frac{UA^3}{OA^3}=\frac{BO}{OA},$

so

$\frac{u^3}{a^3}=\frac{b}{a},\, u^3=a^2b$

as required.

Diocles did not really solve the Delian problem. The reason is that the cissoid of Diocles cannot be constructed perfectly, at least not with compass and straightedge. To construct the cissoid of Diocles, one would construct a finite number of its individual points, then connect all these points to form a curve. The problem is that there is no well-defined way to connect the points. If they are connected by line segments, then the construction will be well-defined, but it will not be an exact cissoid of Diocles, but only an approximation. Likewise, if the dots are connected with circular arcs, the construction will be well-defined, but incorrect. Or one could simply draw a curve directly, trying to eyeball the shape of the curve, but the result would only be imprecise guesswork.

Once the finite set of points on the cissoid have been drawn, then line PC will probably not intersect one of these points exactly, but will pass between them, intersecting the cissoid of Diocles at some point whose exact location has not been constructed, but has only been approximated. An alternative is to keep adding constructed points to the cissoid which get closer and closer to the intersection with line PC, but the number of steps may very well be infinite, and the Greeks did not recognize approximations as limits of infinite steps (so they were very puzzled by Zeno's paradoxes).

One could also construct a cissoid of Diocles by means of a mechanical tool specially designed for that purpose, but this violates the rule of only using compass and straightedge. This rule was established for reasons of logical — axiomatic — consistency. Allowing construction by new tools would be like adding new axioms, but axioms are supposed to be simple and self-evident, but such tools are not. So by the rules of classical, synthetic geometry, Diocles did not solve the Delian problem, which actually can not be solved by such means.

On the other hand, if one accepts that cissoids of Diocles do exist, then there must exist at least one example of such a cissoid. This cissoid could then be translated, rotated, and expanded or contracted in size (without changing its proportional shape) at will to fit into any position. Then one would readily admit that such a cissoid can be used to correctly solve the Delian problem.

Roulette

This curve is also a roulette. Take two congruent parabolas, set them vertex-to-vertex, and roll one along the other; the vertex of the rolling parabola will trace the cissoid.

Figure 1. A pair of parabolas face each other symmetrically: one on top and one on the bottom. Then the top parabola is rolled without slipping along the bottom one, and its successive positions are shown in the animation. Then the path traced by the vertex of the top parabola as it rolls is a roulette shown in red, which happens to be a cissoid of Diocles.

Define a pair of parabolas whose equations are

$y = x^2, \$

$y = -x^2. \$

These parabolas face each other symmetrically across the x-axis, and are the ones shown in Figure 1. Then pick a point (a, a²) from the top parabola. The slope of the tangent to the top parabola at this point is

${d (x^2) \over dx} = 2 x. \$

The distance measured along the top parabola from point (0,0) to point (a, a²) is equivalent to the distance measured along the bottom parabola from point (0,0) to point (a, −a²). Thus, when the top parabola rolls, its point which was originally at (a, a²) will eventually come into tangential contact with the point (a, −a²) of the bottom parabola. This is true for all values of a.

When the two such points are in contact, their tangents coincide and have the same slope, which is −2 a. Let θ be the angle which the slope 2 a makes with the x-axis, so that

$\tan \theta = 2 a \qquad \qquad (1)$.

Then the top parabola must rotate by an angle of 2 θ in order for its point originally at (a, a²) to come into contact with the bottom parabola's point at (a, −a²).

This rotation can be performed by means of the rotation matrix R(−2 θ), viz.

$R(- 2 \theta) = \begin{bmatrix} \cos 2 \theta & \sin 2 \theta \\ -\sin 2 \theta & \cos 2 \theta \end{bmatrix}.$

Let the pivoting point of the rotation be point (a, a²). This pivoting vector must be subtracted from all the points on the top parabola before all these points are operated upon by the rotation matrix. Then, after the rotation is performed, this pivoting point will be at the origin, and the slope of the rotated top parabola at the origin will be −2 a, which corresponds to the slope of the point (a, −a²) of the bottom parabola. These two points must come into contact, so the rotated top parabola will be moved by vector (a, −a²) to its new position in contact with the bottom parabola. Thus the rolled top parabola will be described by

$\begin{bmatrix} \cos 2 \theta & \sin 2 \theta \\ -\sin 2 \theta & \cos 2 \theta \end{bmatrix} \begin{bmatrix} x - a \\ x^2 - a^2 \end{bmatrix} + \begin{bmatrix} a \\ -a^2 \end{bmatrix}$

where a may be called a "rolling parameter" and x is the pre-rotated abscissa.

Applying the trigonometric identities

$\cos \, 2 \theta = 2 \cos^2 \theta - 1 \$

$\sin \, 2 \theta = 2 \sin \theta \cos \theta \$

yields a locus of points of the form

$\begin{bmatrix} 2 \cos^2 \theta - 1 & 2 \sin \theta \cos \theta \\ -2 \sin \theta \cos \theta & 2 \cos^2 \theta - 1 \end{bmatrix} \begin{bmatrix} x - a \\ x^2 - a^2 \end{bmatrix} + \begin{bmatrix} a \\ -a^2 \end{bmatrix},$

which, through application of equation (1), becomes

$\begin{bmatrix} 2 \cos^2 (\tan^{-1} (2 a)) - 1 & 2 \sin (\tan^{-1} (2 a)) \cos(\tan^{-1} (2 a)) \\ -2 \sin (\tan^{-1} (2 a)) \cos (\tan^{-1} (2 a)) & 2 \cos^2 (\tan^{-1} (2 a)) - 1 \end{bmatrix} \begin{bmatrix} x - a \\ x^2 - a^2 \end{bmatrix} + \begin{bmatrix} a \\ -a^2 \end{bmatrix}.$

Then, applying the identities

$\cos \tan^{-1} x = {1 \over \sqrt{1 + x^2}}$

$\sin \tan^{-1} x = {x \over \sqrt{1 + x^2}}$

produces the set of points of the form

$\begin{bmatrix} {2 \over 1 + 4 a^2} - 1 & 2 \left( {2 a \over \sqrt{1 + 4 a^2}} \right) \left( {1 \over \sqrt{1 + 4 a^2}} \right) \\ - {4 a \over 1 + 4 a^2} & {2 \over 1 + 4 a^2} - 1 \end{bmatrix} \begin{bmatrix} x - a \\ x^2 - a^2 \end{bmatrix} + \begin{bmatrix} a \\ -a^2 \end{bmatrix}$

$= \begin{bmatrix} {1 - 4 a^2 \over 1 + 4 a^2} & {4 a \over 1 + 4 a^2} \\ {-4 a \over 1 + 4 a^2} & {1 - 4 a^2 \over 1 + 4 a^2} \end{bmatrix} \begin{bmatrix} x - a \\ x^2 - a^2 \end{bmatrix} + \begin{bmatrix} a \\ -a^2 \end{bmatrix}$

$= \begin{bmatrix} {(1 - 4 a^2) (x - a) + 4 a (x^2 - a^2) \over 1 + 4 a^2} + a \\ {-4 a (x - a) + (x^2 - a^2) (1 - 4 a^2) \over 1 + 4 a^2} - a^2 \end{bmatrix}$

$= \begin{bmatrix} {4 a^3 + 4 a x^2 - 4 a^2 x + x \over 1 + 4 a^2} \\ {2 a^2 + x^2 - 4 a^2 x^2 - 4 a x \over 1 + 4 a^2} \end{bmatrix}.$

The vertex of the rolled top parabola is specified by letting x = 0, which results in the set of points which depend only on the rolling parameter a and whose coordinates are

$X(a) = {4 a^3 \over 1 + 4 a^2}, \qquad \qquad (2)$

$Y(a) = {2 a^2 \over 1 + 4 a^2}. \qquad \qquad (3)$

This curve of points (X(a), Y(a)) is the roulette, and now it only remains to be shown that it is a cissoid of Diocles. The roulette is a cissoid whose equation is

$X^2 = {Y^3 \over {1 \over 2} - Y} \qquad \qquad (4)$.

To demonstrate this, plug in the values of X and Y given in equations (2) and (3) into equation (4) and see if it leads to a tautology:

$\left[ {4 a^3 \over 1 + 4 a^2} \right]^2 = { \left[ {2 a^2 \over 1 + 4 a^2} \right]^3 \over {1 \over 2} - \left[ {2 a^2 \over 1 + 4 a^2} \right]}$

${16 a^6 \over (1 + 4 a^2)^2} = { \left[ {8 a^6 \over (1 + 4 a^2)^3} \right] \over {1 \over 2} - {2 a^2 \over 1 + 4 a^2}}$

${16 a^6 \over (1 + 4 a^2)^2} = { 8 a^6 / (1 + 4 a^2)^3 \over {1 + 4 a^2 \over 2 (1 + 4 a^2)} - {4 a^2 \over 2 (1 + 4 a^2)}}$

${16 a^6 \over (1 + 4 a^2)^2} = {8 a^6 / (1 + 4 a^2)^3 \over {1 \over 2 (1 + 4 a^2)} } = {16 a^6 \over (1 + 4 a^2)^2}$

which is true for all values of a, the rolling parameter.

The cissoid of Diocles as a pedal curve

THEOREM: The pedal curve of a parabola with respect to its vertex is a cissoid of Diocles.

Proof: Any parabola can be rotated and translated so that it will end up being described by the equation

$y = a x^2, \,$

whose slope at point (x, y) is given by the derivative

${dy \over dx} = 2 a x.$

Then the set of points which form the line tangent to the parabola at point (b, a b²) is

$L_1(b) = \{ (b, a b^2) + (u, 2 a b u) = (b + u, a b^2 + 2 a b u) : u \in \mathbb{R} \}$

and the set of points which form the line which is perpendicular to L₁(b) and which passes through the origin is

$L_2(b) = \left\{ \left(v, -{v \over 2 a b} \right) : v \in \mathbb{R} \right\}.$

Notice that L₂(b)′s slope is −1/(2ab) which is perpendicular to L₁(b)′s slope 2ab.

The intersection L₁(b) ∩ L₂(b) can be found by setting up the following system of equations

$b + u = v, \$

$a b^2 + 2 a b u = - {v \over 2 a b}.$

Now solve for u:

$a b^2 + 2 a b u = - {b + u \over 2 a b} = -{1 \over 2 a} - {u \over 2 a b},$

$a b^2 + {1 \over 2 a} = - u \left( 2 a b + {1 \over 2 a b} \right),$

$u = {- a b^2 - {1 \over 2 a} \over 2 a b + {1 \over 2 a b}} = {-2 a^2 b^2 - 1 \over 4 a^2 b + {1 \over b}}$

so that the abscissa v is

$v = b + u = {2 a^2 b^2 \over 4 a^2 b + {1 \over b}}$

and the ordinate is

$-{v \over 2 a b} = { - a b \over 4 a^2 b + {1 \over b}}.$

Thus, the point of intersection is

$\left( {2 a^2 b^2 \over 4 a^2 b + {1 \over b}}, {- a b \over 4 a^2 b + {1 \over b}} \right) = \left( {2 a^2 b^3 \over 4 a^2 b^2 + 1}, {- a b^2 \over 4 a^2 b^2 + 1} \right)$

and this point belongs to the pedal curve of the parabola.

Let

$X = {2 a^2 b^3 \over 4 a^2 b^2 + 1},$

$Y = {- a b^2 \over 4 a^2 b^2 + 1}.$

Then the question is: is there a constant k which does not depend on b (but only on a) such that

$X^2 = {Y^3 \over 2 k - Y}$?

To find out, substitute the values for X and Y:

${4 a^4 b^6 \over (4 a^2 b^2 + 1)^2} = {- a^3 b^6 / (4 a^2 b^2 + 1)^3 \over 2 k + {a b^2 \over 4 a^2 b^2 + 1}}.$

Multiply the numerator and denominator on the right side by (4 a² b² + 1)³,

${4 a^4 b^6 \over (4 a^2 b^2 + 1)^2} = {-a^3 b^6 \over 2 k (4 a^2 b^2 + 1)^3 + a b^2 (4 a^2 b^2 + 1)^2}.$

Cross-multiply,

$8 k a^4 b^6 (4 a^2 b^2 + 1)^3 + 4 a^5 b^8 (4 a^2 b^2 + 1)^2 = - a^3 b^6 (4 a^2 b^2 + 1)^2. \$

Divide by (4 a² b² + 1)²,

$8 k a^4 b^6 (4 a^2 b^2 + 1) + 4 a^5 b^8 = - a^3 b^6. \$

Distribute,

$32 k a^6 b^8 + 8 k a^4 b^6 + 4 a^5 b^8 = - a^3 b^6. \$

Divide both sides by a³ b⁶,

$32 k a^3 b^2 + 8 k a + 4 a^2 b^2 = -1. \,$

Subtract 4 a² b² from both sides, then factor out 8 a k on the left side,

$8 a k (1 + 4 a^2 b^2) = -(1 + 4 a^2 b^2). \,$

Cancel out the common factor on both sides, then solve for k,

$k = - {1 \over 8 a}.$

k does not depend on b, so, for a given parabola (with fixed value of a), k is a constant, and the pedal curve is a cissoid of Diocles.

Inversion

The cissoid of Diocles also be defined as the inverse curve of a parabola with the center of inversion at the vertex. To see this, take the parabola to be x=y². In polar coordinates this becomes

$r=\frac{\cos\theta}{\sin^2\theta}$,

and the inverse curve then has equation

$r=\frac{\sin^2\theta}{\cos\theta} = \sin\theta \tan\theta$

which is a special case of the equation defining the cissoid of Diocles on polar coordinates.

References

1. ^ See Basset for the derivation, many other sources give the construction.
2. ^ Proof is a slightly modified version of that given in Basset.

• J. Dennis Lawrence (1972). A catalog of special plane curves. Dover Publications. pp. 95, 98–100. ISBN 0-486-60288-5. 
• Weisstein, Eric W., "Cissoid of Diocles" from MathWorld.
• "Cissoid of Diocles" at Visual Dictionary Of Special Plane Curves
• "Cissoid of Diocles" at MacTutor's Famous Curves Index
• "Cissoid" on 2dcurves.com
• "Cissoïde de Dioclès ou Cissoïde Droite" at Encyclopédie des Formes Mathématiques Remarquables (in French)
• "The Cissoid" An elementary treatise on cubic and quartic curves Alfred Barnard Basset (1901) Cambridge pp. 85ff