- Origin (mathematics)
-
The origin of a Cartesian coordinate systemIn mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect. In Euclidean geometry, the origin may be chosen freely as any convenient point of reference.
The most common coordinate systems are two-dimensional (contained in a plane) and three-dimensional (contained in a space), composed of two and three perpendicular axes, respectively. The origin divides each of these axes into two halves, a positive and a negative semiaxis. Points can then be located with reference to the origin by giving their numerical coordinates—that is, the positions of their projections along each axis, either in the positive or negative direction. The coordinates of the origin are always all zero, for example (0,0) in two dimensions and (0,0,0) in three.
The origin of the complex plane can be referred as the point where real axis and imaginary axis intersect each other. In other words, it is the point representing 0 + 0i.
Symmetry with respect to the origin
This graph is symmetric with respect to the origin because when reflected over both the x-axis and the y-axis, the graph looks unchanged.
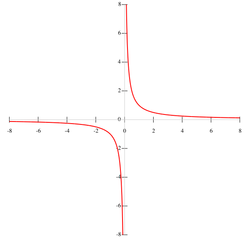
When a graph is symmetric with respect to the origin, it describes a graph that looks the same before and after the graph is rotated 180 degrees. Formally, a graph is symmetric with respect to the origin if it is unchanged when reflected across both the x-axis and y-axis.
The graphs of an invertible function and its inverse always have the line y = x which definitely passes through the origin as the axis of symmetry.
This geometry-related article is a stub. You can help Wikipedia by expanding it.
