Pedal curve

Geometric construction of the pedal of C with respect to P

In the differential geometry of curves, a pedal curve is a curve derived by construction from a given curve (as is, for example, the involute).

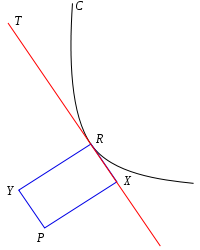
Let C be a given curve and P a fixed point (called the pedal point). At any point R on C let T be the tangent line at R. There is then a unique point X on T which is either P (in case P lies on T) or forms with P a line perpendicular to T. The pedal curve is the set of all such X for all R on C. (The point X is called the foot of the perpendicular to T from P.) Similarly, there is a unique point Y on the line normal to C at R so that PY is perpendicular to the normal, so PXRY is a (possibly degenerate) rectangle. The locus of points Y is called the contrapedal curve.

The orthotomic of a curve is its pedal magnified by a factor of 2 so that the center of similarity is P. This is locus of the reflection of P through the tangent line L

Geometrical properties

Consider a right angle moving rigidly so that one leg remains on the point P and the other leg is tangent to the curve. Then the vertex of this angle is X and traces out the pedal curve. As the angle moves, its direction of motion at P is parallel to PX and its direction of motion at R is parallel to the tangent T = RX. Therefore the instant center of rotation is the intersection of the line perpendicular to PX at P and perpendicular to RX at R, and this point is Y. If follows that the tangent to the pedal at X is perpendicular to XY.

Draw a circle with diameter PR, then it circumscribes rectangle PXRY and XY is another diameter. The circle and the pedal are both perpendicular to XY so they are tangent at X. Hence the pedal is the envelope of the circles with diameters PR where R lies on the curve.

The line YR is normal to the curve and the envelope of such normals is its evolute. Therefore YR is tangent to the evolute and the point Y is the foot of the perpendicular from P to this tangent, in other words Y is on the pedal of the evolute. It follows that the contrapedal of a curve is the pedal of its evolute.

Let C′ be the curve obtained by shrinking C by a factor of 2 toward P. Then the point R′ corresponding to R is the center of the rectangle PXRY, and the tangent to C′ at R′ bisects this rectangle parallel to PY and XR. A ray of light starting from P and reflected by C′ at R' will then pass through Y. The reflected ray, when extended, is the line XY which is perpendicular to the pedal of C. The envelope of lines perpendicular to the pedal is then the envelope of reflected rays or the catacaustic of C′. This proves that the catacaustic of a curve is the evolute of its orthotomic.

As noted earlier, the circle with diameter PR is tangent to the pedal. The center of this circle is R′ which follows the curve C′. It follows that the envelope of circles through a fixed point and whose centers lie on a given curve is the orthotomic of the curve.

Let D′ be a curve congruent to C′ and let D′ roll without slipping, as in the definition of a roulette, on C′ so that D′ is always the reflection of C′ with respect to the line to which they are mutually tangent. Then when the curves touch at R′ the point corresponding to P on the moving plane is X, and so the roulette is the pedal curve. Equivalently, the orthotomic of a curve is the roulette of the curve on its mirror image.

Example

Limaçon — pedal curve of a circle

When C is a circle the above discussion shows that the following definitions of a limaçon are equivalent:

• It is the pedal of a circle.
• It is the envelope of circles whose diameters have one endpoint on a fixed point and another endpoint which follow a circle.
• It is the envelope of circles through a fixed point whose centers follow a circle.
• It is the roulette formed by a circle rolling around a circle with the same radius.

We also have shown that the catacaustic of a circle is the evolute of a limaçon.

Equations

Another example : pedal curve of an ellipse

Contrapedal of the same ellipse

Pedal of the evolute of the ellipse : same as the contrapedal of the original ellipse

Let $\vec{v} = P - R$ be the vector for R to P and write

$\vec{v} = \vec{v}_{\parallel}+\vec{v}_\perp$,

the tangential and normal components of $\vec{v}$ with respect to the curve. Then $\vec{v}_{\parallel}$ is the vector from R to X from which the position of X can be computed.

Specifically, if c is a parametrization of the curve then

$t\mapsto c(t)+{ c'(t) \cdot (P-c(t))\over|c'(t)|^2} c'(t)$

parametrises the pedal curve (disregarding points where c' is zero or undefined).

For a parametrically defined curve, its pedal curve with pedal point (0;0) is defined as

$X[x,y]=\frac{(xy'-yx')y'}{x'^2 + y'^2}$

$Y[x,y]=\frac{(yx'-xy')x'}{x'^2 + y'^2}.$

The contrapedal curve is given by:

$t\mapsto P-{ c'(t) \cdot (P-c(t))\over|c'(t)|^2} c'(t)$

With the same pedal point, the contrapedal curve is the pedal curve of the evolute of the given curve.

given curve	pedal point	pedal curve	contrapedal curve
line	any	point	parallel line
circle	on circumference	cardioid	—
parabola	on axis	conchoid of de Sluze	—
parabola	on tangent of vertex	ophiuride	—
parabola	focus	line	—
other conic section	focus	circle	—
logarithmic spiral	pole	congruent log spiral	congruent log spiral
epicycloid hypocycloid	center	rose	rose
involute of circle	center of circle	Archimedean spiral	the circle

Example

Pedal curves of unit circle:

$c(t)=\begin{bmatrix} \cos(t) \\ \sin(t) \end{bmatrix}$

$c'(t)=\begin{bmatrix} -\sin(t) \\ \cos(t) \end{bmatrix}$   and   | c'(t) | = 1

${ c'(t) \cdot ((x,y)-c(t))\over|c'(t)|^2}=y\cos(t)-x\sin(t)$

thus, the pedal curve with pedal point (x,y) is:

$\begin{bmatrix} \cos(t)-y\cos(t)\sin(t)+x\sin(t)^2 \\ \sin(t)-x\sin(t)\cos(t)+y\cos(t)^2 \end{bmatrix}$

If the pedal point is at the center (i.e. (0,0)), the circle is its own pedal curve. If the pedal point is (1,0) the pedal curve is

$\begin{bmatrix} \cos(t)+\sin(t)^2 \\ \sin(t)-\sin(t)\cos(t)\end{bmatrix}=\begin{bmatrix} 1 \\ 0\end{bmatrix}+(1-\cos(t))\begin{bmatrix} \cos(t) \\ \sin(t) \end{bmatrix}$

i.e. a pedal point on the circumference gives a cardioid.

See also

• List of curves

References

• Weisstein, Eric W., "Pedal Curve" from MathWorld.
• Weisstein, Eric W., "Contrapedal Curve" from MathWorld.
• Weisstein, Eric W., "Orthotomic" from MathWorld.
• Differential and integral calculus: with applications by George Greenhill (1891) p326 ff. (Google books)
• "Podaire d'une Courbe" at Encyclopédie des Formes Mathématiques Remarquables
• "Note on the Problem of Pedal Curves" by Arthur Cayley
• J. Dennis Lawrence (1972). A catalog of special plane curves. Dover Publications. p. 60. ISBN 0-486-60288-5.