Orbit of the Moon

Not to be confused with Lunar orbit in the sense of a selenocentric orbit, that is, an orbit around the Moon

The Moon completes its orbit around the Earth in approximately 27.3 days (a sidereal month). The Earth and Moon orbit about their barycentre (common centre of mass), which lies about 4700 km from Earth's centre (about three quarters of the Earth's radius). On average, the Moon is at a distance of about 385000 km from the centre of the Earth, which corresponds to about 60 Earth radii. With a mean orbital velocity of 1.023 km/s, the Moon moves relative to the stars each hour by an amount roughly equal to its angular diameter, or by about 0.5°. The Moon differs from most satellites of other planets in that its orbit is close to the plane of the ecliptic, and not to the Earth's equatorial plane. The lunar orbit plane is inclined to the ecliptic by about 5.1°, whereas the Moon's spin axis is inclined by only 1.5°.

Property	Value
Semi-major axis [1]	384748 km [2]
mean distance [3]	385000 km [4]
inverse sine parallax [5]	384400 km
Distance at perigee	~362600 km (356400-370400 km)
Distance at apogee	~405400 km (404000-406700 km)
Mean eccentricity	0.0549006 (0.026 – 0.077)[6]
Mean inclination of orbit to ecliptic	5.14° (4.99 – 5.30)[6]
Mean obliquity	6.58°
Mean inclination of lunar equator to ecliptic	1.543°
Period of precession of nodes	18.5996 years
Period of recession of line of apsides	8.8504 years

Properties

Lunar perigee–apogee size comparison

Earth's lunar orbit perturbation basics

Definition of orbital parameters.

The properties of the orbit described in this section are approximations. The Moon's orbit around the Earth has many irregularities (perturbations), whose study (lunar theory) has a long history.^[7]

Elliptic shape

The orbit of the Moon is distinctly elliptical with an average eccentricity of 0.0549. The non-circular form of the lunar orbit causes variations in the Moon's angular speed and apparent size as it moves towards and away from an observer on Earth. The mean angular daily movement relative to an imaginary observer at the barycentre is 13.176° to the east (Julian Day 2000.0 rate).

Line of apsides

The orientation of the orbit is not fixed in space, but precesses over time. The nearest and farthest points in the orbit are the perigee and apogee respectively. The line joining these two points (the line of apsides) rotates slowly in the same direction as the Moon itself (direct motion), making one complete revolution in 3232.6054 days or about 8.85 solar orbits.

Elongation

The Moon's elongation is its angular distance east of the Sun at any time. At new moon it is zero and the Moon is said to be in conjunction. At full moon the elongation is 180° and it is said to be in opposition. In both cases the Moon is in syzygy, that is, the Sun, Moon and Earth are nearly aligned. When elongation is either 90° or 270° the Moon is said to be in quadrature.

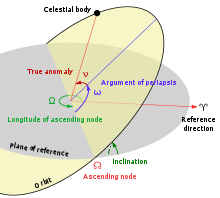
Nodes

The nodes are points at which the Moon's orbit crosses the ecliptic. The Moon crosses the same node every 27.2122 days, an interval called the draconic or draconitic month. The line of nodes is the intersection between the two respective planes. It has a retrograde motion: for an observer on Earth it rotates westward along the ecliptic with a period of 18.6 years, or 19°21′ per year. When viewed from celestial north, the nodes move clockwise around the Earth, opposite the Earth's own spin and its rotation around the Sun. Lunar and solar eclipses can only occur when the line of nodes points toward the Sun, roughly every 5.4 months. The type of the eclipse depends on Moon's orbital position in that time window.

Inclination

The mean inclination of the lunar orbit to the ecliptic plane is 5.145°. The rotation axis of the Moon is also not perpendicular to its orbital plane, so the lunar equator is not in the plane of its orbit, but is inclined to it by a constant value of 6.688° (this is the obliquity). One might be tempted to think that as a result of the precession of the Moon's orbital plane, the angle between the lunar equator and the ecliptic would vary between the sum (11.833°) and difference (1.543°) of these two angles. However, as was discovered by Jacques Cassini in 1721, the rotation axis of the Moon precesses with the same rate as its orbital plane, but is 180° out of phase (see Cassini's Laws). Thus, although the rotation axis of the Moon is not fixed with respect to the stars, the angle between the ecliptic and the lunar equator is always 1.543°.

Lunar standstill

When the ascending node of the Moon's orbit coincides with the vernal equinox in the northern hemisphere, the declination of the Moon in the sky reaches a maximum at 23°29′ + 5°9′ or 28°36′. This is called the major standstill. Nine and a half years later, when the descending node has come to the same point, the angle is only 23°28′ − 5°8′ or 18°19′, and the declination of the Moon is a minimum. This is the minor standstill.

Double planet?

Some consider the Earth–Moon system to be a double planet because of the relatively large size of the Moon; the Earth–Moon mass ratio, about 81:1, is much smaller than that of most other natural satellites in the Solar System. An informal criterion for a double planet system is that its barycentre must be exterior to both bodies. By that criterion, the Earth and Moon are an ordinary planet–moon system, because their mutual distance is about 60 Earth radii but their mass ratio is 81:1 so their centre of mass always lies well within the Earth.

The Moon orbiting Earth with sizes and distances to scale. Each pixel represents 500 km.

History of observations and measurements

About 3000 years ago, the Babylonians were the first human civilization to keep a consistent record of lunar observations. Clay tablets from that time period found over the territory of present-day Iraq are inscribed with cuneiform recording the times and dates of moonrises and moonsets, the stars that the Moon passed close by, and the time differences between rising and setting of both the Sun and the Moon around the time of the full moon. The Babylonians discovered the three main periods of the Moon's motion and used data analysis to build lunar calendars that extended well into the future.^[7] This use of detailed, systematic observations to make predictions based on experimental data may be classified as the first scientific study in human history. However, Babylonians seem to have lacked any geometrical or physical interpretation of their data, and they could not predict future lunar eclipses (although "warnings" were issued before likely eclipse times).

Ancient Greek astronomers were the first to introduce and analyze mathematical models of the motion of objects in the sky. Ptolemy described lunar motion by using a well-defined geometric model of epicycles and evection.^[7]

Isaac Newton was the first to develop a complete theory of motion, mechanics. The sheer wealth of humanity's observations of the lunar motion was the main testbed of his theory.^[7]

Lunar periods

See also: Month

Name	Value (days)	Definition
sidereal month	27.32166155	with respect to the distant stars (13.36874634 passes per solar orbit)
synodic month	29.53058886	with respect to the Sun (phases of the Moon, 12.36874634 passes per solar orbit)
tropical month	27.321582	with respect to the vernal point (precesses in ~26,000 years)
anomalistic month	27.554550	with respect to the perigee (recesses in 3232.6054 days = 8.8504 years)
draconic (nodical) month	27.212220815	with respect to the ascending node (precesses in 6793.4765 days = 18.5996 years)

There are several ways to measure how much time it takes the Moon to complete one orbit. The sidereal month is the time it takes to make one complete orbit with respect to the fixed stars, which is about 27.3 days. In contrast, the synodic month is the time it takes the Moon to reach the same phase, which takes about 29.5 days. The synodic period is longer than the sidereal period because the Earth–Moon system moves a finite distance in its orbit around the Sun during each sidereal month, and a longer time is required to achieve the same relative geometry. Other definitions for the duration of a lunar month include the time it takes to go from perigee to perigee (the anomalistic month), from ascending node to ascending node (the draconic month), and from two successive passes of the same ecliptic longitude (the tropical month). As a result of the slow precession of the lunar orbit, these latter three periods are only slightly different from the sidereal month. The average length of a calendric month (¹⁄₁₂ of a year) is about 30.4 days.

Tidal evolution

See also: Tide, Tidal acceleration, and Axial tilt#Long period variations

The gravitational attraction that the Moon exerts on Earth is the major cause of tides in the sea; the Sun has a lesser tidal influence. If the Earth possessed a global ocean of uniform depth, the Moon would act to deform both the solid earth (by a small amount) and ocean in the shape of an ellipsoid with high points directly beneath the Moon and on the opposite side of the Earth. However, as a result of the irregular coastline and varying ocean depths, this idealization is only partially realized. While the tidal flow period is generally synchronized to the Moon's orbit around Earth, its phase can vary. In some places on Earth there is only one high tide per day, though this is somewhat rare.

The tidal bulges on Earth are carried ahead of the Earth–Moon axis by a small amount as a result of the Earth's rotation. This is a direct consequence of friction and the dissipation of energy as water moves over the ocean bottom and into or out of bays and estuaries. Each bulge exerts a small amount of gravitational attraction on the Moon, with the bulge closest to the Moon pulling in a direction slightly forward along the Moon's orbit, because the Earth's rotation has carried the bulge forward. The opposing bulge has the opposite effect, but the closer bulge dominates due to its comparative closer distance to the Moon. As a result, some of the Earth's rotational momentum is gradually being transferred to the Moon's orbital momentum, and this causes the Moon to slowly recede from Earth at the rate of approximately 38 millimetres per year. In keeping with the conservation of angular momentum, the Earth's rotation is gradually slowing, and the Earth's day thus lengthens by about 23 microseconds every year (excluding glacial rebound). Both figures are valid only for the current configuration of the continents. Tidal rhythmites from 620 million years ago show that over hundreds of millions of years the Moon receded at an average rate of 22 millimetres per year and the day lengthened at an average rate of 12 microseconds per year, both about half of their current values. See tidal acceleration for a more detailed description and references.

The Moon is gradually receding from the Earth into a higher orbit, and calculations^[8][9] suggest that this would continue for about fifty billion years. By that time, the Earth and Moon would become caught up in what is called a "spin–orbit resonance" in which the Moon will circle the Earth in about 47 days (currently 27 days), and both Moon and Earth would rotate around their axes in the same time, always facing each other with the same side. However, the slowdown of the Earth's rotation is not occurring fast enough for the rotation to lengthen to a month before other effects change the situation: about 2.1 billion years from now, the increase of the Sun's radiation will have caused the Earth's oceans to vaporize, removing the bulk of the tidal friction and acceleration.^{[citation needed]}

Libration

Animation of the Moon as it cycles through its phases. The apparent wobbling of the Moon is known as libration.

The Moon is in synchronous rotation, meaning that it keeps the same face turned toward the Earth at all times. This synchronous rotation is only true on average, because the Moon's orbit has a definite eccentricity. As a result, the angular velocity of the Moon varies as it moves around the Earth, and is hence not always equal to the Moon's rotational velocity. When the Moon is at its perigee, its rotation is slower than its orbital motion, and this allows us to see up to eight degrees of longitude of its eastern (right) far side. Conversely, when the Moon reaches its apogee, its rotation is faster than its orbital motion and this reveals eight degrees of longitude of its western (left) far side. This is referred to as longitudinal libration.

Because the lunar orbit is also inclined to the Earth's ecliptic plane by 5.1°, the rotation axis of the Moon seems to rotate towards and away from us during one complete orbit. This is referred to as latitudinal libration, which allows one to see almost 7° of latitude beyond the pole on the far side. Finally, because the Moon is only about 60 Earth radii away from the Earth's centre of mass, an observer at the equator who observes the Moon throughout the night moves laterally by one Earth diameter. This gives rise to a diurnal libration, which allows one to view an additional one degree's worth of lunar longitude. For the same reason, observers at both geographical poles of the Earth would be able to see one additional degree's worth of libration in latitude.

Path of Earth and Moon around Sun

The Moon's orbital path around the Sun (accompanying the Earth in its own path around the Sun) is always convex outwards.^[10] (In this diagram, the Sun is below and to the left of the frame.)

When viewed from the north celestial pole, i.e. from the star Polaris, the Moon orbits the Earth counterclockwise, the Earth orbits the Sun counterclockwise, and the Moon and Earth rotate on their own axes counterclockwise.

The right-hand rule may be used instead. If the thumb of the right hand points to the north celestial pole, its fingers curl in the direction that the Moon orbits the Earth, the Earth orbits the Sun, and the direction the Moon and Earth rotate on their own axes.

In representations of the Solar System, it is common to draw the trajectory of the Earth from the point of view of the Sun, and the trajectory of the Moon from the point of view of the Earth. This could give the impression that the Moon circles around the Earth in such a way that sometimes it goes backwards when viewed from the Sun's perspective. Since the orbital velocity of the Moon about the Earth (1 km/s) is small compared to the orbital velocity of the Earth about the Sun (30 km/s), this never occurs.

Considering the Earth-Moon system as a binary planet, their mutual centre of gravity is within the Earth, about 4624 km from its centre or 72.6% of its radius. This centre of gravity remains in line towards the Moon as the Earth completes its diurnal rotation. It is this mutual centre of gravity which defines the path of the Earth-Moon system in solar orbit. Consequently the Earth's centre veers inside and outside the orbital path during each synodic month as the Moon moves in the opposite direction.

Unlike most other moons in the Solar System, the trajectory of the Moon is very similar to that of its planet. The Sun's gravitational pull on the Moon is over twice as great as the Earth's pull on the Moon; consequently, the Moon's trajectory is always convex^[11][12] (as seen when looking inward at the entire Moon/Earth/Sun system from a great distance off), and is nowhere concave (from the perspective just mentioned) or looped.^[10][11][13] If the gravitational attraction of the Sun could be "turned off" while maintaining the Earth-Moon gravitational attraction, the Moon would continue to orbit the Earth once every sidereal month.

See also

Moon portal

• Lunar theory
• Ernest William Brown
• Orbital elements
• Lunar Laser Ranging Experiment
• List of orbits
• Milankovitch cycles
• Supermoon

References

1. ^ The geometric mean distance in the orbit (of ELP)
2. ^ M. Chapront-Touzé, J. Chapront (1983). "The lunar ephemeris ELP-2000". Astronomy & Astrophysics 124: 54. Bibcode 1983A&A...124...50C. 
3. ^ The constant in the ELP expressions for the distance, which is the mean distance averaged over time
4. ^ M. Chapront-Touzé, J. Chapront (1988). "ELP2000-85: a semi-analytical lunar ephemeris adequate for historical times". Astronomy & Astrophysics 190: 351. Bibcode 1988A&A...190..342C. 
5. ^ This often quoted value for the mean distance is actually the inverse of the mean of the inverse of the distance, which is not the same as the mean distance itself.
6. ^ ^{a b} Jean Meeus, Mathematical astronomy morsels (Richmond, VA: Willmann-Bell, 1997) 11–12.
7. ^ ^{a b c d} Martin C. Gutzwiller (1998). "Moon-Earth-Sun: The oldest three-body problem". Reviews of Modern Physics 70 (2): 589–639. Bibcode 1998RvMP...70..589G. doi:10.1103/RevModPhys.70.589. 
8. ^ C.D. Murray & S.F. Dermott (1999). Solar System Dynamics. Cambridge University Press. p. 184. 
9. ^ Dickinson, Terence (1993). From the Big Bang to Planet X. Camden East, Ontario: Camden House. pp. 79–81. ISBN 0-921820-71-2. 
10. ^ ^{a b} The reference by H L Vacher (2001)(details separately cited in this list) describes this as 'convex outward', while older references such as "The Moon's Orbit Around the Sun, Turner, A. B. Journal of the Royal Astronomical Society of Canada, Vol. 6, p.117, 1912JRASC...6..117T"; and "H Godfray, Elementary Treatise on the Lunar Theory" describe the same geometry by the words concave to the sun.
11. ^ ^{a b} "The Orbit of the Moon around the Sun is Convex!". http://www.math.nus.edu.sg/aslaksen/teaching/convex.html. Retrieved 2006-04-21. 
12. ^ The Moon Always Veers Toward the Sun at MathPages
13. ^ Vacher, H.L. (November 2001). "Computational Geology 18 - Definition and the Concept of Set" (PDF). Journal of Geoscience Education 49 (5): 470–479. http://www.nagt.org/files/nagt/jge/columns/CG18-v49n5p470.pdf. Retrieved 2006-04-21.