Celestial coordinate system

For other uses of "Celestial", see Celestial (disambiguation).

Orientation of Astronomical Coordinates

Orientation of the galactic, ecliptic and equatorial coordinate systems, projected on the celestial sphere, showing the galactic equator (black), north galactic pole (NGP), the ecliptic (orange), north ecliptic pole (NEP), the celestial equator (blue) and north celestial pole (NCP). Sun and earth not shown to scale but to indicate sun's orbital direction around the galactic center and earth's orbital direction around the sun.

In astronomy, a celestial coordinate system is a coordinate system for mapping positions on the celestial sphere. There are different celestial coordinate systems each using a system of spherical coordinates projected on the celestial sphere, in analogy to the geographic coordinate system used on the surface of the Earth.^[1] The coordinate systems differ only in their choice of the fundamental plane, which divides the sky into two equal hemispheres along a great circle. For example, the fundamental plane of the geographic system is the Earth's equator. Each coordinate system is named for its choice of fundamental plane.

Coordinate systems

The following table lists the standard coordinate systems in use by the astronomy community. The fundamental plane divides the sphere into two equal hemispheres and defines the baseline for the equivalent latitude in the coordinates. This defines equivalent to the equator in the geographic coordinate system (GCS). The two points located 90° from the fundamental plane are termed the poles. The coordinate column gives the coordinate system's equivalents to the latitude and longitude in GCS, respectively.

Coordinate system [2]	Fundamental plane	Poles	Coordinates
Horizontal (also called Alt/Az or Az/El)	horizon	zenith/nadir	elevation (also called altitude) - azimuth - meridian
Equatorial	celestial equator	celestial poles	declination - right ascension or hour angle
Ecliptic	ecliptic	ecliptic poles	ecliptic latitude - ecliptic longitude
Galactic	galactic plane	galactic poles	galactic latitude - galactic longitude
Supergalactic	supergalactic plane	Supergalactic poles	supergalactic latitude, supergalactic longitude

Horizontal system

Main article: Horizontal coordinate system

The horizontal, or altitude-azimuth, system is based on the position of the observer on Earth, which revolves around its own axis once per sidereal day (23.hours, 56 minutes and 4.091 seconds) in relation to the "fixed" star background. The positioning of a celestial object by the horizontal system varies with time, but is a useful coordinate system for locating and tracking objects for observers on earth. It is based on the position of stars relative to an observer's ideal horizon.

Equatorial system

Main article: Equatorial coordinate system

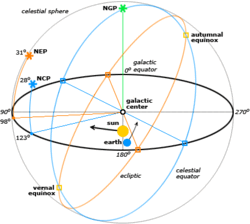
The equatorial coordinate system is centered at Earth's center, but fixed relative to distant stars and galaxies. The coordinates are based on the location of stars relative to Earth's equator if it were projected out to an infinite distance. The equatorial describes the sky as seen from the solar system, and modern star maps almost exclusively use equatorial coordinates.

The equatorial system is the normal coordinate system for most professional and many amateur astronomers having an equatorial mount that follows the movement of the sky during the night. Celestial objects are found by adjusting the telescope's or other instrument's scales so that they match the equatorial coordinates of the selected object to observe.

Popular choices of pole and equator are the older B1950 and the modern J2000 systems, but a pole and equator "of date" can also be used, meaning one appropriate to the date under consideration, such as that at which a measurement of the position of a planet or spacecraft is made. There are also subdivisions into "mean of date" coordinates, which average out or ignore nutation, and "true of date," which include nutation.

Ecliptical system

Main article: Ecliptic coordinate system

The ecliptic system was one of the old coordinate systems used for star maps before astronomy and astrology divorced, particularly in the West.

The ecliptic system describes the planets' orbital movement around the sun, and centers on the barycenter of the solar system (i.e. very close to the sun). The fundamental plane is the plane of the Earth's orbit, called the ecliptic plane. The system is primarily used for computing the positions of planets and other solar system bodies, as well as defining their orbital elements.

Galactic system

Main article: Galactic coordinate system

The galactic coordinate system uses the approximate plane of our galaxy as its fundamental plane. The solar system is still the center of the coordinate system, and the zero point is defined as the direction towards the galactic center. Galactic latitude resembles the elevation above the galactic plane and galactic longitude determines direction relative to the center of the galaxy.

Supergalactic system

Main article: Supergalactic coordinate system

The supergalactic coordinate system corresponds to a fundamental plane which contains a higher than average number of local galaxies in the sky as seen from Earth.

Converting coordinates

Equatorial to horizontal coordinates

Let H be the hour angle and δ the declination in equatorial coordinates. Suppose the need is to compute the altitude a and the azimuth A in horizontal coordinates. Then, for an observer at latitude Φ, the conversion equations are:

$\sin \mathrm{a} = \cos \theta = \sin \phi \cdot \sin \delta + \cos \phi \cdot \cos \delta \cdot \cos H$

$\cos \mathrm{A} = \frac{\cos \phi \cdot \sin \delta - \sin \phi \cdot \cos \delta \cdot \cos H}{\cos \mathrm{a}}.$

where θ is the zenith angle (or zenith distance, i.e. the 90° complement of Altitude). The inverse trigonometric functions are then used to get the values of the coordinates.

NOTE: Inverse cosine is dual valued, i.e. 160° and 200° both have the same cosine. The above needs to be corrected. If H < 180 (or Pi radians) then Az = 360 - Az as derived from the above equation.

See also

• Axial tilt
• Azimuth
• Inclination
• Kozai effect
• Orbital inclination change

References

1. ^ Schombert, James. "Earth Coordinate System". University of Oregon Department of Physics. http://abyss.uoregon.edu/~js/ast121/lectures/lec03.html. Retrieved 19 March 2011. 
2. ^ Majewski, Steve. "Coordinate Systems". UVa Department of Astronomy. http://www.astro.virginia.edu/class/majewski/astr551/lectures/COORDS/coords.html. Retrieved 19 March 2011. 

External links

• This article was originally based on Jason Harris' Astroinfo which comes along with KStars, a KDE Desktop Planetarium for Linux/KDE.