Axial tilt

"Obliquity" redirects here. For the book, see Obliquity (book).

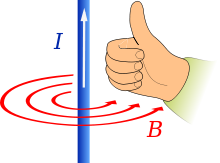To understand axial tilt, consider this blue solenoid in right hand grip rule as the rotational axis of Earth, the counter-clockwise direction of the magnetic field as the 'orbital plane' of Earth and the direction of the thumb pointing toward the north pole of Earth. In this figure, 'axial tilt' is zero degrees because the rotational axis is perpendicular to the orbital plane. If this blue solenoid (rotational axis) is tilted while the orbital plane remains fixed, then it is called the axial tilt of the planet or celestial body.

In astronomy, axial tilt (also called obliquity) is the angle between an object's rotational axis, and a line perpendicular to its orbital plane. It differs from inclination.

To measure obliquity, use the right hand grip rule for both the rotation and the orbital motion, i.e.: the line from the vertex at the object's centre to its north pole (above which the object appears to rotate counter-clockwise); and the line drawn from the vertex in the direction of the normal to its orbital plane, (above which the object moves counter-clockwise in its orbit). At zero degrees, these lines point in the same direction.

The planet Venus has an axial tilt of 177.3° because it is rotating in retrograde direction, opposite to other planets like Earth. The north pole of Venus is pointed 'downward' (our southward). The planet Uranus is rotating on its side in such a way that its rotational axis, and hence its north pole, is pointed almost in the direction of its orbit around the Sun. Hence the axial tilt of Uranus is 97°.^[1]

Over the course of an orbit, while the angle of the axial tilt does not change, the orientation of a planet's axial tilt moves through 360 degrees (one complete orbit around the Sun), relative to a line between the planet and the Sun, causing seasons on Earth.

Obliquity

Earth's axial tilt is 23.44°.^[2]

In the solar system, the Earth's orbital plane is known as the ecliptic plane, and so the Earth's axial tilt is officially called the obliquity of the ecliptic. It is denoted by the Greek letter ε.

The Earth currently has an axial tilt of about 23.5°.^[2] The axis remains tilted in the same direction towards the stars throughout a year and this means that when a hemisphere (a northern or southern half of the earth) is pointing away from the Sun at one point in the orbit then half an orbit later (half a year later) this hemisphere will be pointing towards the Sun. This effect is the main cause of the seasons (see effect of sun angle on climate). Whichever hemisphere is currently tilted toward the Sun experiences more hours of sunlight each day, and the sunlight at midday also strikes the ground at an angle nearer the vertical and thus delivers more energy per unit surface area.

Lower obliquity causes polar regions to receive less seasonally contrasting solar radiation, producing conditions more favorable to glaciation. Like changes in precession and eccentricity, changes in tilt influence the relative strength of the seasons, but the effects of the tilt cycle are particularly pronounced in the high latitudes where the great ice ages began.^[3] Obliquity is a major factor in glacial/interglacial fluctuations (see Milankovitch cycles).

The obliquity of the ecliptic is not a fixed quantity but changing over time in a cycle with a period of 41,000 years (see below). Note that the obliquity and the precession of the equinoxes are calculated from the same theory and are thus related to each other. A smaller ε means a larger p (precession in longitude) and vice versa. Yet the two movements act independent from each other, going in mutually perpendicular directions.

Measurement

Knowledge of the obliquity of the ecliptic (ε) is critical for astronomical calculations and observations from the surface of the Earth (Earth-based, positional astronomy).

To quickly grasp an idea of its numerical value one can look at how the Sun's angle above the horizon varies with the seasons. The measured difference between the angles of the Sun above the horizon at noon on the longest and shortest days of the year gives twice the obliquity.

To an observer on the equator standing all year long looking above, the sun will be directly overhead at noon on the March Equinox, then swing north until it is over the Tropic of Cancer, 23° 26’ away from the equator on the Northern Solstice. On the September Equinox it will be back overhead, then swing south until it is over the Tropic of Capricorn, 23° 26’ away from the equator on the Southern Solstice.

Example: an observer at 50° latitude (either north or south) will see the Sun 63° 26’ above the horizon at noon on the longest day of the year, but only 16° 34’ on the shortest day. The difference is 2ε = 46° 52’, and so ε = 23° 26’.

(90° - 50°) + 23.4394° = 63.4394° when measuring angles from the horizon (90° - 50°) − 23.4394° = 16.5606°

At the Equator, this would be 90° + 23.4394° = 113.4394° and 90° − 23.4394° = 66.5606° (measuring always from the southern horizon).

Abu-Mahmud Khojandi measured the Earth's axial tilt in the 10th century using this principle with a giant sextant and noted that his value was lower than those of earlier astronomers, thus discovering that the axial tilt is not constant.^[4]

Values

The Earth's axial tilt varies between 22.1° and 24.5° (but see below), with a 41,000 year period, and at present, the tilt is decreasing. In addition to this steady decrease there are much smaller short term (18.6 years) variations, known as nutation, mainly due to the changing plane of the moon's orbit. This can shift the Earth's axial tilt by plus or minus 0.005 degree.

Simon Newcomb's calculation at the end of the nineteenth century for the obliquity of the ecliptic gave a value of 23° 27’ 8.26” (epoch of 1900), and this was generally accepted until improved telescopes allowed more accurate observations, and electronic computers permitted more elaborate models to be calculated. Lieske developed an updated model in 1976 with ε equal to 23° 26’ 21.448” (epoch of 2000), which is part of the approximation formula recommended by the International Astronomical Union in 2000:

ε = 84381.448 − 46.84024T − (59 × 10⁻⁵)T² + (1.813 × 10⁻³)T³, measured in seconds of arc, with T being the time in Julian centuries (that is, 36,525 days) since the ephemeris epoch of 2000 (which occurred on Julian day 2,451,545.0). A straight application of this formula to 1900 (T=-1) returns 23° 27’ 8.29”, which is very close to Newcomb's value.

With the linear term in T being negative, at present the obliquity is slowly decreasing. It is implicit that this expression gives only an approximate value for ε and is only valid for a certain range of values of T. If not, ε would approach infinity as T approaches infinity. Computations based on a numerical model of the solar system show that ε has a period of about 41,000 years, the same as the constants of the precession p of the equinoxes (although not of the precession itself).

Other theoretical models may come with values for ε expressed with higher powers of T, but since no (finite) polynomial can ever represent a periodic function, they all go to either positive or negative infinity for large enough T. In that respect one can understand the decision of the International Astronomical Union to choose the simplest equation which agrees with most models. For up to 5,000 years in the past and the future all formulas agree, and up to 9,000 years in the past and the future, most agree to reasonable accuracy. For eras farther out discrepancies get too large.

Long period variations

See also: Orbit of the Moon (Tidal evolution of the lunar orbit).

Nevertheless extrapolation of the average polynomials gives a fit to a sine curve with a period of 41,013 years, which, according to Wittmann, is equal to:

ε = A + B sin(C(T + D)); with A = 23.496932° ± 0.001200°, B = − 0.860° ± 0.005°, C = 0.01532 ± 0.0009 radian/Julian century, D = 4.40 ± 0.10 Julian centuries, and T, the time in centuries from the epoch of 2000 as above.

This means a range of the obliquity from 22° 38’ to 24° 21’, the last maximum was reached in 8700 BC, the mean value occurred around 1550 and the next minimum will be in 11800. This formula should give a reasonable approximation for the previous and next million years or so. Yet it remains an approximation in which the amplitude of the wave remains the same, while in reality, as seen from the results of the Milankovitch cycles, irregular variations occur. The quoted range for the obliquity is from 21° 30’ to 24° 30’, but the low value may have been a one-time overshot of the normal 22° 30’.^{[citation needed]}

Over the last 5 million years, the obliquity of the ecliptic (or more accurately, the obliquity of the Equator on the moving ecliptic of date) has varied from 22.0425° to 24.5044°, but for the next one million years, the range will be only from 22.2289° to 24.3472°.^{[citation needed]}

Other planets may have a variable obliquity, too; for example, on Mars, the range is believed to be between 11° and 49° as a result of gravitational perturbations from other planets.^[5] The relatively small range for the Earth is due to the stabilizing influence of the Moon, but it will not remain so. According to W.R. Ward, the orbit of the Moon (which is continuously increasing due to tidal effects) will have gone from the current 60 to approximately 66.5 Earth radii in about 1.5 billion years. Once this occurs, a resonance from planetary effects will follow, causing swings of the obliquity between 22° and 38°. Further, in approximately 2 billion years, when the Moon reaches a distance of 68 Earth radii, another resonance will cause even greater oscillations, between 27° and 60°. This would have extreme effects on climate.

Axial tilt of selected objects in the solar system

Object	Axial tilt (°)	Axial tilt (radians)
Sun	7.25	0.1265
Mercury	0.0352	0.000614
Venus	177.4	3.096
Earth	23.44	0.4091
Moon	6.688†	0.1167
Mars	25.19	0.4396
Ceres	~4	~0.07
Pallas	~60	~1
Jupiter	3.13	0.0546
Saturn	26.73	0.4665
Uranus	97.77	1.7064
Neptune	28.32	0.4943
Pluto	119.61	2.0876

† Tilt to its orbit in the Earth-Moon system. Moon's tilt is 1.5424° (0.02692 radians) to ecliptic

See also

Celestial equator Celestial pole Ecliptic Milankovitch cycles Nutation

Orbital plane Polar motion Retrograde motion Rotation axis True polar wander

Solar System portal

References

1. ^ http://nssdc.gsfc.nasa.gov/planetary/factsheet/planetfact_notes.html
2. ^ ^{a b} Staff (2007-08-07). "Useful Constants". International Earth Rotation and Reference Systems Service (IERS). http://hpiers.obspm.fr/eop-pc/models/constants.html. Retrieved 2008-09-23. 
3. ^ Paleo Slide Sets
4. ^ Al-Khujandī, Abū Maḥmūd Ḥāmid Ibn Al-Khiḍr, Complete Dictionary of Scientific Biography, 2008
5. ^ Touma, Jihad; Wisdom, Jack (1993). "The Chaotic Obliquity of Mars". Science 259 (5099): 1294. Bibcode 1993Sci...259.1294T. doi:10.1126/science.259.5099.1294. PMID 17732249. 

External links

• Explanatory supplement to "the Astronomical ephemeris" and the American Ephemeris and Nautical Almanac
• A comparison of values predicted by different theories at tenspheres.com
• Berger, A. L. "Obliquity & precession for the last 5 million years". Astronomy & Astrophysics 51, 127 (1976)
• Wittmann, A. "The obliquity of the ecliptic". Astronomy & Astrophysics 73, 129-131 (1979)
• Ward, W. R. "Comments on the long-term stability of the Earth's obliquity". Icarus 1982, 50, 444
• National Space Science Data Center
• Bryant, Jeff. Axial Tilts of Planets, Wolfram Demonstrations Project