- Cryptographic hash function
-
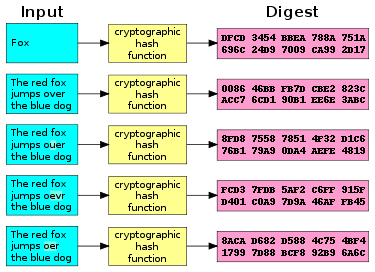 A cryptographic hash function (specifically, SHA-1) at work. Note that even small changes in the source input (here in the word "over") drastically change the resulting output, by the so-called avalanche effect.
A cryptographic hash function (specifically, SHA-1) at work. Note that even small changes in the source input (here in the word "over") drastically change the resulting output, by the so-called avalanche effect.
A cryptographic hash function is a deterministic procedure that takes an arbitrary block of data and returns a fixed-size bit string, the (cryptographic) hash value, such that an accidental or intentional change to the data will change the hash value. The data to be encoded is often called the "message," and the hash value is sometimes called the message digest or simply digest.
The ideal cryptographic hash function has four main or significant properties:
- it is easy (but not necessarily quick) to compute the hash value for any given message
- it is infeasible to generate a message that has a given hash
- it is infeasible to modify a message without changing the hash
- it is infeasible to find two different messages with the same hash
Cryptographic hash functions have many information security applications, notably in digital signatures, message authentication codes (MACs), and other forms of authentication. They can also be used as ordinary hash functions, to index data in hash tables, for fingerprinting, to detect duplicate data or uniquely identify files, and as checksums to detect accidental data corruption. Indeed, in information security contexts, cryptographic hash values are sometimes called (digital) fingerprints, checksums, or just hash values, even though all these terms stand for functions with rather different properties and purposes.
Contents
Properties
Most cryptographic hash functions are designed to take a string of any length as input and produce a fixed-length hash value.
A cryptographic hash function must be able to withstand all known types of cryptanalytic attack. As a minimum, it must have the following properties:
- Preimage resistance
- Given a hash
 it should be difficult to find any message
it should be difficult to find any message  such that
such that  . This concept is related to that of one-way function. Functions that lack this property are vulnerable to preimage attacks.
. This concept is related to that of one-way function. Functions that lack this property are vulnerable to preimage attacks.
- Given a hash
- Second-preimage resistance
- Given an input
 it should be difficult to find another input
it should be difficult to find another input  — where
— where  — such that
— such that  . This property is sometimes referred to as weak collision resistance, and functions that lack this property are vulnerable to second-preimage attacks.
. This property is sometimes referred to as weak collision resistance, and functions that lack this property are vulnerable to second-preimage attacks.
- Given an input
- Collision resistance
- It should be difficult to find two different messages
 and
and  such that
such that  . Such a pair is called a cryptographic hash collision. This property is sometimes referred to as strong collision resistance. It requires a hash value at least twice as long as that required for preimage-resistance, otherwise collisions may be found by a birthday attack.
. Such a pair is called a cryptographic hash collision. This property is sometimes referred to as strong collision resistance. It requires a hash value at least twice as long as that required for preimage-resistance, otherwise collisions may be found by a birthday attack.
- It should be difficult to find two different messages
These properties imply that a malicious adversary cannot replace or modify the input data without changing its digest. Thus, if two strings have the same digest, one can be very confident that they are identical.
A function meeting these criteria may still have undesirable properties. Currently popular cryptographic hash functions are vulnerable to length-extension attacks: given
 and
and  but not
but not  , by choosing a suitable
, by choosing a suitable  an attacker can calculate
an attacker can calculate  where | | denotes concatenation.[citation needed] This property can be used to break naive authentication schemes based on hash functions. The HMAC construction works around these problems.
where | | denotes concatenation.[citation needed] This property can be used to break naive authentication schemes based on hash functions. The HMAC construction works around these problems.Ideally, one may wish for even stronger conditions. It should be impossible for an adversary to find two messages with substantially similar digests; or to infer any useful information about the data, given only its digest. Therefore, a cryptographic hash function should behave as much as possible like a random function while still being deterministic and efficiently computable.
Checksum algorithms, such as CRC32 and other cyclic redundancy checks, are designed to meet much weaker requirements, and are generally unsuitable as cryptographic hash functions. For example, a CRC was used for message integrity in the WEP encryption standard, but an attack was readily discovered which exploited the linearity of the checksum.
Degree of difficulty
In cryptographic practice, “difficult” generally means “almost certainly beyond the reach of any adversary who must be prevented from breaking the system for as long as the security of the system is deemed important.” The meaning of the term is therefore somewhat dependent on the application, since the effort that a malicious agent may put into the task is usually proportional to his expected gain. However, since the needed effort usually grows very quickly with the digest length, even a thousand-fold advantage in processing power can be neutralized by adding a few dozen bits to the latter.
In some theoretical analyses “difficult” has a specific mathematical meaning, such as not solvable in asymptotic polynomial time. Such interpretations of difficulty are important in the study of provably secure cryptographic hash functions but do not usually have a strong connection to practical security. For example, an exponential time algorithm can sometimes still be fast enough to make a feasible attack. Conversely, a polynomial time algorithm (e.g. one that requires n20 steps for n-digit keys) may be too slow for any practical use.
Illustration
An illustration of the potential use of a cryptographic hash is as follows: Alice poses a tough math problem to Bob, and claims she has solved it. Bob would like to try it himself, but would yet like to be sure that Alice is not bluffing. Therefore, Alice writes down her solution, appends a random nonce, computes its hash and tells Bob the hash value (whilst keeping the solution and nonce secret). This way, when Bob comes up with the solution himself a few days later, Alice can prove that she had the solution earlier by revealing the nonce to Bob. (This is an example of a simple commitment scheme; in actual practice, Alice and Bob will often be computer programs, and the secret would be something less easily spoofed than a claimed puzzle solution).
Applications
Verifying the integrity of files or messages
An important application of secure hashes is verification of message integrity. Determining whether any changes have been made to a message (or a file), for example, can be accomplished by comparing message digests calculated before, and after, transmission (or any other event).
For this reason, most digital signature algorithms only confirm the authenticity of a hashed digest of the message to be "signed." Verifying the authenticity of a hashed digest of the message is considered proof that the message itself is authentic.
A related application is password verification. Passwords are usually not stored in cleartext, for obvious reasons, but instead in digest form. To authenticate a user, the password presented by the user is hashed and compared with the stored hash.
File or data identifier
A message digest can also serve as a means of reliably identifying a file; several source code management systems, including Git, Mercurial and Monotone, use the sha1sum of various types of content (file content, directory trees, ancestry information, etc.) to uniquely identify them. Hashes are used to identify files on peer-to-peer filesharing networks. For example, in an ed2k link, an MD4-variant hash is combined with the file size, providing sufficient information for locating file sources, downloading the file and verifying its contents. Magnet links are another example. Such file hashes are often the top hash of a hash list or a hash tree which allows for additional benefits.
One of the main applications of a hash function is to allow the fast look-up of a data in a hash table. Being hash functions of a particular kind, cryptographic hash functions lend themselves well to this application too.
However, compared with standard hash functions, cryptographic hash functions tend to be much more expensive computationally. For this reason, they tend to be used in contexts where it is necessary for users to protect themselves against the possibility of forgery (the creation of data with the same digest as the expected data) by potentially malicious participants.
Pseudorandom generation and key derivation
Hash functions can also be used in the generation of pseudorandom bits, or to derive new keys or passwords from a single, secure key or password.
Hash functions based on block ciphers
There are several methods to use a block cipher to build a cryptographic hash function, specifically a one-way compression function.
The methods resemble the block cipher modes of operation usually used for encryption. All well-known hash functions, including MD4, MD5, SHA-1 and SHA-2 are built from block-cipher-like components designed for the purpose, with feedback to ensure that the resulting function is not bijective. SHA-3 finalists include functions with block-cipher-like components (e.g., Skein, BLAKE) and functions based on other designs (e.g., JH, Keccak).
A standard block cipher such as AES can be used in place of these custom block ciphers; that might be useful when an embedded system needs to implement both encryption and hashing with minimal code size or hardware area. However, that approach can have costs in efficiency and security. The ciphers in hash functions are built for hashing: they use large keys and blocks, can efficiently change keys every block, and have been designed and vetted for resistance to related-key attacks. General-purpose ciphers tend to have different design goals. In particular, AES has key and block sizes that make it nontrivial to use to generate long hash values; AES encryption becomes less efficient when the key changes each block; and related-key attacks make it potentially less secure for use in a hash function than for encryption.
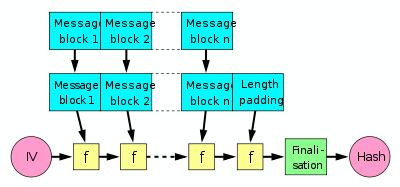
Merkle–Damgård construction
A hash function must be able to process an arbitrary-length message into a fixed-length output. This can be achieved by breaking the input up into a series of equal-sized blocks, and operating on them in sequence using a one-way compression function. The compression function can either be specially designed for hashing or be built from a block cipher. A hash function built with the Merkle–Damgård construction is as resistant to collisions as is its compression function; any collision for the full hash function can be traced back to a collision in the compression function.
The last block processed should also be unambiguously length padded; this is crucial to the security of this construction. This construction is called the Merkle–Damgård construction. Most widely used hash functions, including SHA-1 and MD5, take this form.
The construction has certain inherent flaws, including length-extension and generate-and-paste attacks, and cannot be parallelized. As a result, many entrants in the current NIST hash function competition are built on different, sometimes novel, constructions.
Use in building other cryptographic primitives
Hash functions can be used to build other cryptographic primitives. For these other primitives to be cryptographically secure, care must be taken to build them correctly.
Message authentication codes (MACs) (also called keyed hash functions) are often built from hash functions. HMAC is such a MAC.
Just as block ciphers can be used to build hash functions, hash functions can be used to build block ciphers. Luby-Rackoff constructions using hash functions can be provably secure if the underlying hash function is secure. Also, many hash functions (including SHA-1 and SHA-2) are built by using a special-purpose block cipher in a Davies-Meyer or other construction. That cipher can also be used in a conventional mode of operation, without the same security guarantees. See SHACAL, BEAR and LION.
Pseudorandom number generators (PRNGs) can be built using hash functions. This is done by combining a (secret) random seed with a counter and hashing it.
Some hash functions, such as Skein, Keccak, and RadioGatún output an arbitrarily long stream and can be used as a stream cipher, and stream ciphers can also be built from fixed-length digest hash functions. Often this is done by first building a cryptographically secure pseudorandom number generator and then using its stream of random bytes as keystream. SEAL is a stream cipher that uses SHA-1 to generate internal tables, which are then used in a keystream generator more or less unrelated to the hash algorithm. SEAL is not guaranteed to be as strong (or weak) as SHA-1.
Concatenation of cryptographic hash functions
Concatenating outputs from multiple hash functions provides collision resistance as good as the strongest of the algorithms included in the concatenated result. For example, older versions of TLS/SSL use concatenated MD5 and SHA-1 sums; that ensures that a method to find collisions in one of the functions doesn't allow forging traffic protected with both functions.
For Merkle-Damgård hash functions, the concatenated function is as collision-resistant as its strongest component,[1] but not more collision-resistant.[2] Joux[3] noted that 2-collisions lead to n-collisions: if it is feasible to find two messages with the same MD5 hash, it is effectively no more difficult to find as many messages as the attacker desires with identical MD5 hashes. Among the n messages with the same MD5 hash, there is likely to be a collision in SHA-1. The additional work needed to find the SHA-1 collision (beyond the exponential birthday search) is polynomial. This argument is summarized by Finney. A more current paper and full proof of the security of such a combined construction gives a clearer and more complete explanation of the above.[4]
Cryptographic hash algorithms
There is a long list of cryptographic hash functions, although many have been found to be vulnerable and should not be used. Even if a hash function has never been broken, a successful attack against a weakened variant thereof may undermine the experts' confidence and lead to its abandonment. For instance, in August 2004 weaknesses were found in a number of hash functions that were popular at the time, including SHA-0, RIPEMD, and MD5. This has called into question the long-term security of later algorithms which are derived from these hash functions — in particular, SHA-1 (a strengthened version of SHA-0), RIPEMD-128, and RIPEMD-160 (both strengthened versions of RIPEMD). Neither SHA-0 nor RIPEMD are widely used since they were replaced by their strengthened versions.
As of 2009, the two most commonly used cryptographic hash functions are MD5 and SHA-1. However, MD5 has been broken; an attack against it was used to break SSL in 2008.[5]
The SHA-0 and SHA-1 hash functions were developed by the NSA. In February 2005, a successful attack on SHA-1 was reported, finding collisions in about 269 hashing operations, rather than the 280 expected for a 160-bit hash function. In August 2005, another successful attack on SHA-1 was reported, finding collisions in 263 operations. Theoretical weaknesses of SHA-1 exist as well,[6][7] suggesting that it may be practical to break within years. New applications can avoid these problems by using more advanced members of the SHA family, such as SHA-2, or using techniques such as randomized hashing[8][9] that do not require collision resistance.
However, to ensure the long-term robustness of applications that use hash functions, there is a competition to design a replacement for SHA-2, which will be given the name SHA-3 and become a FIPS standard around 2012.[10]
Some of the following algorithms are used often in cryptography; consult the article for each specific algorithm for more information on the status of each algorithm. Note that this list does not include candidates in the current NIST hash function competition. For additional hash functions see the box at the bottom of the page.
Algorithm Output size (bits) Internal state size Block size Length size Word size Collision attacks (complexity) Preimage attacks (complexity) GOST 256 256 256 256 32 Yes (2105) Yes (2192) HAVAL 256/224/192/160/128 256 1024 64 32 Yes MD2 128 384 128 No 32 Yes (263.3) Yes (273) MD4 128 128 512 64 32 Yes (3) Yes (270.4) MD5 128 128 512 64 32 Yes (220.96) Yes (2123.4) PANAMA 256 8736 256 No 32 Yes RadioGatún up to 608/1216 (19 words) 58 words 3 words No 1-64 With flaws (2352 or 2704) RIPEMD 128 128 512 64 32 Yes (218) RIPEMD-128/256 128/256 128/256 512 64 32 No RIPEMD-160/320 160/320 160/320 512 64 32 No SHA-0 160 160 512 64 32 Yes (233.6) SHA-1 160 160 512 64 32 Yes (251) No SHA-256/224 256/224 256 512 64 32 No No SHA-512/384 512/384 512 1024 128 64 No No Tiger(2)-192/160/128 192/160/128 192 512 64 64 Yes (262:19) Yes (2184.3) WHIRLPOOL 512 512 512 256 8 Yes ([1]) Note: The internal state here means the "internal hash sum" after each compression of a data block. Most hash algorithms also internally use some additional variables such as length of the data compressed so far since that is needed for the length padding in the end. See the Merkle-Damgård construction for details.
See also
- Avalanche effect
- Comparison of cryptographic hash functions
- CRYPTREC and NESSIE - Projects which recommend hash functions
- Keyed-hash message authentication code
- MD5CRK
- Message authentication code
- PGP word list
- Provably secure cryptographic hash function
- SHA-3
- UOWHF - Universal One Way Hash Functions
- Hash chain
References
- ^ Note that any two messages that collide the concatenated function also collide each component function, by the nature of concatenation. For example, if concat(sha1(message1), md5(message1)) == concat(sha1(message2), md5(message2)) then sha1(message1) == sha1(message2) and md5(message1)==md5(message2). The concatenated function could have other problems that the strongest hash lacks -- for example, it might leak information about the message when the strongest component does not, or it might be detectably nonrandom when the strongest component is not -- but it can't be less collision-resistant.
- ^ More generally, if an attack can produce a collision in one hash function's internal state, attacking the combined construction is only as difficult as a birthday attack against the other function(s). For the detailed argument, see the Joux and Finney references that follow.
- ^ Antoine Joux. Multicollisions in Iterated Hash Functions. Application to Cascaded Constructions. LNCS 3152/2004, pages 306-316 Full text.
- ^ Jonathan J. Hoch and Adi Shamir (2008-02-20). On the Strength of the Concatenated Hash Combiner when all the Hash Functions are Weak. http://eprint.iacr.org/2008/075.pdf.
- ^ Alexander Sotirov, Marc Stevens, Jacob Appelbaum, Arjen Lenstra, David Molnar, Dag Arne Osvik, Benne de Weger, MD5 considered harmful today: Creating a rogue CA certificate, accessed March 29, 2009
- ^ Xiaoyun Wang, Yiqun Lisa Yin, and Hongbo Yu, Finding Collisions in the Full SHA-1
- ^ Bruce Schneier, Cryptanalysis of SHA-1 (summarizes Wang et al. results and their implications)
- ^ Shai Halevi, Hugo Krawczyk, Update on Randomized Hashing
- ^ Shai Halevi and Hugo Krawczyk, Randomized Hashing and Digital Signatures
- ^ NIST.gov - Computer Security Division - Computer Security Resource Center
Further reading
- Bruce Schneier. Applied Cryptography. John Wiley & Sons, 1996. ISBN 0-471-12845-7.
- Christof Paar, Jan Pelzl, "Hash Functions", Chapter 11 of "Understanding Cryptography, A Textbook for Students and Practitioners". (companion web site contains online cryptography course that covers hash functions), Springer, 2009.
Cryptographic hash functions and message authentication codes (MACs) Common functions Functions SHA-3 finalists BLAKE · Grøstl · JH · Keccak · SkeinMAC algorithms Authenticated
encryption modesAttacks Misc. Standardization Cryptography Symmetric-key algorithm · Block cipher · Stream cipher · Public-key cryptography · Cryptographic hash function · Message authentication code · Random numbers · SteganographyCategories:- Cryptography
- Cryptographic primitives
- Cryptographic hash functions
- Hashing
Wikimedia Foundation. 2010.