Checksum

Effect of a typical checksum function (the Unix cksum utility).

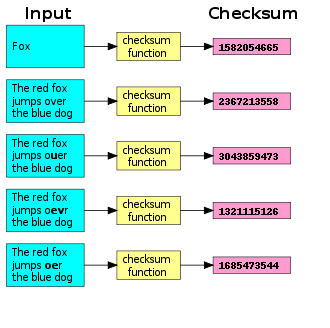
A checksum or hash sum is a fixed-size datum computed from an arbitrary block of digital data for the purpose of detecting accidental errors that may have been introduced during its transmission or storage. The integrity of the data can be checked at any later time by recomputing the checksum and comparing it with the stored one. If the checksums match, the data were almost certainly not altered (either intentionally or unintentionally).

The procedure that yields the checksum from the data is called a checksum function or checksum algorithm. A good checksum algorithm will yield a different result with high probability when the data is accidentally corrupted; if the checksums match, the data is very likely to be free of accidental errors.

Checksum functions are related to hash functions, fingerprints, randomization functions, and cryptographic hash functions. However, each of those concepts has different applications and therefore different design goals. Check digits and parity bits are special cases of checksums, appropriate for small blocks of data (such as Social Security numbers, bank account numbers, computer words, single bytes, etc.). Some error-correcting codes are based on special checksums that not only detect common errors but also allow the original data to be recovered in certain cases.

Checksum algorithms

Parity byte or parity word

The simplest checksum algorithm is the so-called longitudinal parity check, which breaks the data into "words" with a fixed number n of bits, and then computes the exclusive or of all those words. The result is appended to the message as an extra word. To check the integrity of a message, the receiver computes the exclusive or of all its words, including the checksum; if the result is not a word with n zeros, the receiver knows that a transmission error occurred.

With this checksum, any transmission error that flips a single bit of the message, or an odd number of bits, will be detected as an incorrect checksum. However, an error that affects two bits will not be detected if those bits lie at the same position in two distinct words. If the affected bits are independently chosen at random, the probability of a two-bit error being undetected is 1/n.

Modular sum

A variant of the previous algorithm is to add all the "words" as unsigned binary numbers, discarding any overflow bits, and append the two's complement of the total as the checksum. To validate a message, the receiver adds all the words in the same manner, including the checksum; if the result is not a word full of zeros, an error must have occurred. This variant too detects any single-bit error, but the probability that a two-bit error will go undetected is a little less than 1/n.

Position-dependent checksums

The simple checksums described above fail to detect some common errors that affect many bits at once, such as changing the order of data words, or inserting or deleting words with all bits set to zero. The checksum algorithms that are most used in practice, such as Fletcher's checksum, Adler-32, and cyclic redundancy checks (CRCs), address these weaknesses by considering not only the value of each word but also its position in the sequence. This feature generally increases the cost of computing the checksum.

General considerations

A message that is m bits long can be viewed as a corner of the m-dimensional hypercube. The effect of a checksum algorithm that yields an n-bit checksum is to map each m-bit message to a corner of a larger hypercube, with dimension m+n. The 2^m+n corners of this hypercube represent all possible received messages. The valid received messages (those that have the correct checksum) comprise a smaller set, with only 2^m corners.

A single-bit transmission error then corresponds to a displacement from a valid corner (the correct message and checksum) to one of the m adjacent corners. An error that affects k bits moves the message to a corner that is k steps removed from its correct corner. The goal of a good checksum algorithm is to spread the valid corners as far from each other as possible, so as to increase the likelihood that "typical" transmission errors will end up in an invalid corner.

Checksum tools

• cksum, a Unix command that generates both a 32-bit CRC and a byte count for any given input file.
• Bitser, a free Microsoft Windows application that calculates MD5, SHA-1 and SHA-256 sums for any given input file.
• md5sum, a Unix command that generates an MD5 sum
• jdigest, a Java GUI tool that generates and checks MD5 and SHA sums
• Jacksum, a Java API, usable both through a GUI and a CLI, which incorporates many checksum implementations and allows to extend with as many as you need.
• jcksum, a Java library, that can be used by developers in Java applications to calculate checksums using different algorithms.

See also

• Check digit
• File verification
• Hamming code
• List of hash functions
• Luhn algorithm
• Verhoeff algorithm
• Parity bit
• Frame check sequence
• Bit rot
• ZFS A file system that performs automatic file integrity checking using checksums

External links

• Additive Checksums (C)