- Digital signature
-
This article is about secure cryptographic signatures. For simple signatures in digital form, see Electronic signature.
A digital signature or digital signature scheme is a mathematical scheme for demonstrating the authenticity of a digital message or document. A valid digital signature gives a recipient reason to believe that the message was created by a known sender, and that it was not altered in transit. Digital signatures are commonly used for software distribution, financial transactions, and in other cases where it is important to detect forgery or tampering.
Contents
Explanation
Digital signatures are often used to implement electronic signatures, a broader term that refers to any electronic data that carries the intent of a signature,[1] but not all electronic signatures use digital signatures.[2][3][4] In some countries, including the United States, India,[5] and members of the European Union, electronic signatures have legal significance. However, laws concerning electronic signatures do not always make clear whether they are digital cryptographic signatures in the sense used here, leaving the legal definition, and so their importance, somewhat confused.
Digital signatures employ a type of asymmetric cryptography. For messages sent through a nonsecure channel, a properly implemented digital signature gives the receiver reason to believe the message was sent by the claimed sender. Digital signatures are equivalent to traditional handwritten signatures in many respects; properly implemented digital signatures are more difficult to forge than the handwritten type. Digital signature schemes in the sense used here are cryptographically based, and must be implemented properly to be effective. Digital signatures can also provide non-repudiation, meaning that the signer cannot successfully claim they did not sign a message, while also claiming their private key remains secret; further, some non-repudiation schemes offer a time stamp for the digital signature, so that even if the private key is exposed, the signature is valid nonetheless. Digitally signed messages may be anything representable as a bitstring: examples include electronic mail, contracts, or a message sent via some other cryptographic protocol.
Definition
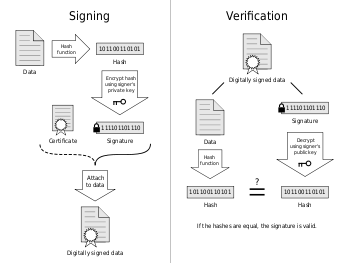
Main article: Public-key cryptographyA digital signature scheme typically consists of three algorithms:
- A key generation algorithm that selects a private key uniformly at random from a set of possible private keys. The algorithm outputs the private key and a corresponding public key.
- A signing algorithm that, given a message and a private key, produces a signature.
- A signature verifying algorithm that, given a message, public key and a signature, either accepts or rejects the message's claim to authenticity.
Two main properties are required. First, a signature generated from a fixed message and fixed private key should verify the authenticity of that message by using the corresponding public key. Secondly, it should be computationally infeasible to generate a valid signature for a party who does not possess the private key.
History
In 1976, Whitfield Diffie and Martin Hellman first described the notion of a digital signature scheme, although they only conjectured that such schemes existed.[6][7] Soon afterwards, Ronald Rivest, Adi Shamir, and Len Adleman invented the RSA algorithm, which could be used to produce primitive digital signatures[8] (although only as a proof-of-concept—"plain" RSA signatures are not secure[9]). The first widely marketed software package to offer digital signature was Lotus Notes 1.0, released in 1989, which used the RSA algorithm.[citation needed]
To create RSA signature keys, generate an RSA key pair containing a modulus N that is the product of two large primes, along with integers e and d such that e d ≡ 1 (mod φ(N)), where φ is the Euler phi-function. The signer's public key consists of N and e, and the signer's secret key contains d.
To sign a message m, the signer computes σ ≡ md (mod N). To verify, the receiver checks that σe ≡ m (mod N).
As noted earlier, this basic scheme is not very secure. To prevent attacks, one can first apply a cryptographic hash function to the message m and then apply the RSA algorithm described above to the result. This approach can be proven secure in the so-called random oracle model[clarification needed].
Other digital signature schemes were soon developed after RSA, the earliest being Lamport signatures,[10] Merkle signatures (also known as "Merkle trees" or simply "Hash trees"),[11] and Rabin signatures.[12]
In 1988, Shafi Goldwasser, Silvio Micali, and Ronald Rivest became the first to rigorously define the security requirements of digital signature schemes.[13] They described a hierarchy of attack models for signature schemes, and also present the GMR signature scheme, the first that can be proven to prevent even an existential forgery against a chosen message attack.[13]
Most early signature schemes were of a similar type: they involve the use of a trapdoor permutation, such as the RSA function, or in the case of the Rabin signature scheme, computing square modulo composite n. A trapdoor permutation family is a family of permutations, specified by a parameter, that is easy to compute in the forward direction, but is difficult to compute in the reverse direction without already knowing the private key. However, for every parameter there is a "trapdoor" (private key) which when known, easily decrypts the message. Trapdoor permutations can be viewed as public-key encryption systems, where the parameter is the public key and the trapdoor is the secret key, and where encrypting corresponds to computing the forward direction of the permutation, while decrypting corresponds to the reverse direction. Trapdoor permutations can also be viewed as digital signature schemes, where computing the reverse direction with the secret key is thought of as signing, and computing the forward direction is done to verify signatures. Because of this correspondence, digital signatures are often described as based on public-key cryptosystems, where signing is equivalent to decryption and verification is equivalent to encryption, but this is not the only way digital signatures are computed.
Used directly, this type of signature scheme is vulnerable to a key-only existential forgery attack. To create a forgery, the attacker picks a random signature σ and uses the verification procedure to determine the message m corresponding to that signature.[14] In practice, however, this type of signature is not used directly, but rather, the message to be signed is first hashed to produce a short digest that is then signed. This forgery attack, then, only produces the hash function output that corresponds to σ, but not a message that leads to that value, which does not lead to an attack. In the random oracle model, this hash-and-decrypt form of signature is existentially unforgeable, even against a chosen-message attack.[7][clarification needed]
There are several reasons to sign such a hash (or message digest) instead of the whole document.
- For efficiency: The signature will be much shorter and thus save time since hashing is generally much faster than signing in practice.
- For compatibility: Messages are typically bit strings, but some signature schemes operate on other domains (such as, in the case of RSA, numbers modulo a composite number N). A hash function can be used to convert an arbitrary input into the proper format.
- For integrity: Without the hash function, the text "to be signed" may have to be split (separated) in blocks small enough for the signature scheme to act on them directly. However, the receiver of the signed blocks is not able to recognize if all the blocks are present and in the appropriate order.
Notions of security
In their foundational paper, Goldwasser, Micali, and Rivest lay out a hierarchy of attack models against digital signatures[13]:
- In a key-only attack, the attacker is only given the public verification key.
- In a known message attack, the attacker is given valid signatures for a variety of messages known by the attacker but not chosen by the attacker.
- In an adaptive chosen message attack, the attacker first learns signatures on arbitrary messages of the attacker's choice.
They also describe a hierarchy of attack results[13]:
- A total break results in the recovery of the signing key.
- A universal forgery attack results in the ability to forge signatures for any message.
- A selective forgery attack results in a signature on a message of the adversary's choice.
- An existential forgery merely results in some valid message/signature pair not already known to the adversary.
The strongest notion of security, therefore, is security against existential forgery under an adaptive chosen message attack.
Uses of digital signatures
As organizations move away from paper documents with ink signatures or authenticity stamps, digital signatures can provide added assurances of the evidence to provenance, identity, and status of an electronic document as well as acknowledging informed consent and approval by a signatory. The United States Government Printing Office (GPO) publishes electronic versions of the budget, public and private laws, and congressional bills with digital signatures. Universities including Penn State, University of Chicago, and Stanford are publishing electronic student transcripts with digital signatures.
Below are some common reasons for applying a digital signature to communications:
Authentication
Although messages may often include information about the entity sending a message, that information may not be accurate. Digital signatures can be used to authenticate the source of messages. When ownership of a digital signature secret key is bound to a specific user, a valid signature shows that the message was sent by that user. The importance of high confidence in sender authenticity is especially obvious in a financial context. For example, suppose a bank's branch office sends instructions to the central office requesting a change in the balance of an account. If the central office is not convinced that such a message is truly sent from an authorized source, acting on such a request could be a grave mistake.
Integrity
In many scenarios, the sender and receiver of a message may have a need for confidence that the message has not been altered during transmission. Although encryption hides the contents of a message, it may be possible to change an encrypted message without understanding it. (Some encryption algorithms, known as nonmalleable ones, prevent this, but others do not.) However, if a message is digitally signed, any change in the message after signature will invalidate the signature. Furthermore, there is no efficient way to modify a message and its signature to produce a new message with a valid signature, because this is still considered to be computationally infeasible by most cryptographic hash functions (see collision resistance).
Non-repudiation
Non-repudiation, or more specifically non-repudiation of origin, is an important aspect of digital signatures. By this property an entity that has signed some information cannot at a later time deny having signed it. Similarly, access to the public key only does not enable a fraudulent party to fake a valid signature.
Additional security precautions
Putting the private key on a smart card
All public key / private key cryptosystems depend entirely on keeping the private key secret. A private key can be stored on a user's computer, and protected by a local password, but this has two disadvantages:
- the user can only sign documents on that particular computer
- the security of the private key depends entirely on the security of the computer
A more secure alternative is to store the private key on a smart card. Many smart cards are designed to be tamper-resistant (although some designs have been broken, notably by Ross Anderson and his students). In a typical digital signature implementation, the hash calculated from the document is sent to the smart card, whose CPU encrypts the hash using the stored private key of the user, and then returns the encrypted hash. Typically, a user must activate his smart card by entering a personal identification number or PIN code (thus providing two-factor authentication). It can be arranged that the private key never leaves the smart card, although this is not always implemented. If the smart card is stolen, the thief will still need the PIN code to generate a digital signature. This reduces the security of the scheme to that of the PIN system, although it still requires an attacker to possess the card. A mitigating factor is that private keys, if generated and stored on smart cards, are usually regarded as difficult to copy, and are assumed to exist in exactly one copy. Thus, the loss of the smart card may be detected by the owner and the corresponding certificate can be immediately revoked. Private keys that are protected by software only may be easier to copy, and such compromises are far more difficult to detect.
Using smart card readers with a separate keyboard
Entering a PIN code to activate the smart card commonly requires a numeric keypad. Some card readers have their own numeric keypad. This is safer than using a card reader integrated into a PC, and then entering the PIN using that computer's keyboard. Readers with a numeric keypad are meant to circumvent the eavesdropping threat where the computer might be running a keystroke logger, potentially compromising the PIN code. Specialized card readers are also less vulnerable to tampering with their software or hardware and are often EAL3 certified.
Other smart card designs
Smart card design is an active field, and there are smart card schemes which are intended to avoid these particular problems, though so far with little security proofs.
Using digital signatures only with trusted applications
One of the main differences between a digital signature and a written signature is that the user does not "see" what he signs. The user application presents a hash code to be encrypted by the digital signing algorithm using the private key. An attacker who gains control of the user's PC can possibly replace the user application with a foreign substitute, in effect replacing the user's own communications with those of the attacker. This could allow a malicious application to trick a user into signing any document by displaying the user's original on-screen, but presenting the attacker's own documents to the signing application.
To protect against this scenario, an authentication system can be set up between the user's application (word processor, email client, etc.) and the signing application. The general idea is to provide some means for both the user app and signing app to verify each other's integrity. For example, the signing application may require all requests to come from digitally signed binaries.
WYSIWYS
Main article: WYSIWYSTechnically speaking, a digital signature applies to a string of bits, whereas humans and applications "believe" that they sign the semantic interpretation of those bits. In order to be semantically interpreted the bit string must be transformed into a form that is meaningful for humans and applications, and this is done through a combination of hardware and software based processes on a computer system. The problem is that the semantic interpretation of bits can change as a function of the processes used to transform the bits into semantic content. It is relatively easy to change the interpretation of a digital document by implementing changes on the computer system where the document is being processed. From a semantic perspective this creates uncertainty about what exactly has been signed. WYSIWYS (What You See Is What You Sign) [15] means that the semantic interpretation of a signed message cannot be changed. In particular this also means that a message cannot contain hidden information that the signer is unaware of, and that can be revealed after the signature has been applied. WYSIWYS is a desirable property of digital signatures that is difficult to guarantee because of the increasing complexity of modern computer systems.
Digital signatures vs. ink on paper signatures
An ink signature could be replicated from one document to another by copying the image manually or digitally, but to have credible signature copies that can resist some scrutiny is a significant manual or technical skill, and to produce ink signature copies that resist professional scrutiny is very difficult.
Digital signatures cryptographically bind an electronic identity to an electronic document and the digital signature cannot be copied to another document. Paper contracts sometimes have the ink signature block on the last page, and the previous pages may be replaced after a signature is applied. Digital signatures can be applied to an entire document, such that the digital signature on the last page will indicate tampering if any data on any of the pages have been altered, but this can also be achieved by signing with ink all pages of the contract.
Additionally, most digital certificates provided by certificate authorities to end users to sign documents can be obtained by at most gaining access to a victim's email inbox.
Important paper documents are signed in ink with all involved parties meeting in person, with additional identification forms other than the actual presence (like driver's licence, passports, fingerprints, etc.), and most usually with the presence of a respected notary that knows the involved parties, the signing often happens in a building which has security cameras and other forms of identification and physical security. The security that is added by these type of ink on paper signatures cannot be currently matched by digital only signatures.
Some digital signature algorithms
- RSA-based signature schemes, such as RSA-PSS
- DSA and its elliptic curve variant ECDSA
- ElGamal signature scheme as the predecessor to DSA, and variants Schnorr signature and Pointcheval–Stern signature algorithm
- Rabin signature algorithm
- Pairing-based schemes such as BLS
- Undeniable signatures
- Aggregate signature - a signature scheme that supports aggregation: Given n signatures on n messages from n users, it is possible to aggregate all these signatures into a single signature whose size is constant in the number of users. This single signature will convince the verifier that the n users did indeed sign the n original messages.
The current state of use — legal and practical
Digital signature schemes share basic prerequisites that— regardless of cryptographic theory or legal provision— they need to have meaning:
-
- Quality algorithms
- Some public-key algorithms are known to be insecure, practicable attacks against them having been discovered.
-
- Quality implementations
- An implementation of a good algorithm (or protocol) with mistake(s) will not work.
-
- The private key must remain private
- if it becomes known to any other party, that party can produce perfect digital signatures of anything whatsoever.
-
- The public key owner must be verifiable
- A public key associated with Bob actually came from Bob. This is commonly done using a public key infrastructure and the public key
 user association is attested by the operator of the PKI (called a certificate authority). For 'open' PKIs in which anyone can request such an attestation (universally embodied in a cryptographically protected identity certificate), the possibility of mistaken attestation is non trivial. Commercial PKI operators have suffered several publicly known problems. Such mistakes could lead to falsely signed, and thus wrongly attributed, documents. 'closed' PKI systems are more expensive, but less easily subverted in this way.
user association is attested by the operator of the PKI (called a certificate authority). For 'open' PKIs in which anyone can request such an attestation (universally embodied in a cryptographically protected identity certificate), the possibility of mistaken attestation is non trivial. Commercial PKI operators have suffered several publicly known problems. Such mistakes could lead to falsely signed, and thus wrongly attributed, documents. 'closed' PKI systems are more expensive, but less easily subverted in this way.
-
- Users (and their software) must carry out the signature protocol properly.
Only if all of these conditions are met will a digital signature actually be any evidence of who sent the message, and therefore of their assent to its contents. Legal enactment cannot change this reality of the existing engineering possibilities, though some such have not reflected this actuality.
Legislatures, being importuned by businesses expecting to profit from operating a PKI, or by the technological avant-garde advocating new solutions to old problems, have enacted statutes and/or regulations in many jurisdictions authorizing, endorsing, encouraging, or permitting digital signatures and providing for (or limiting) their legal effect. The first appears to have been in Utah in the United States, followed closely by the states Massachusetts and California. Other countries have also passed statutes or issued regulations in this area as well and the UN has had an active model law project for some time. These enactments (or proposed enactments) vary from place to place, have typically embodied expectations at variance (optimistically or pessimistically) with the state of the underlying cryptographic engineering, and have had the net effect of confusing potential users and specifiers, nearly all of whom are not cryptographically knowledgeable. Adoption of technical standards for digital signatures have lagged behind much of the legislation, delaying a more or less unified engineering position on interoperability, algorithm choice, key lengths, and so on what the engineering is attempting to provide.
- See also: ABA digital signature guidelines
Industry standards
Some industries have established common interoperability standards for the use of digital signatures between members of the industry and with regulators. These include the Automotive Network Exchange for the automobile industry and the SAFE-BioPharma Association for the healthcare industry.
Using separate key pairs for signing and encryption
In several countries, a digital signature has a status somewhat like that of a traditional pen and paper signature, like in the EU digital signature legislation. Generally, these provisions mean that anything digitally signed legally binds the signer of the document to the terms therein. For that reason, it is often thought best to use separate key pairs for encrypting and signing. Using the encryption key pair, a person can engage in an encrypted conversation (e.g., regarding a real estate transaction), but the encryption does not legally sign every message he sends. Only when both parties come to an agreement do they sign a contract with their signing keys, and only then are they legally bound by the terms of a specific document. After signing, the document can be sent over the encrypted link. If a signing key is lost or compromised, it can be revoked to mitigate any future transactions. If an encryption key is lost, a backup or key escrow should be utilized to continue viewing encrypted content. Signing keys should never be backed up or escrowed.
See also
- Digital certificate
- Public key infrastructure
- Digital signatures and law
- Electronic signature
- Global Trust Center
- GNU Privacy Guard
Notes
- ^ US ESIGN Act of 2000
- ^ The University of Virginia
- ^ State of WI
- ^ National Archives of Australia
- ^ The Information Technology Act, 2000. http://www.dot.gov.in/Acts/itbill2000.pdf.
- ^ "New Directions in Cryptography", IEEE Transactions on Information Theory, IT-22(6):644–654, Nov. 1976.
- ^ a b "Signature Schemes and Applications to Cryptographic Protocol Design", Anna Lysyanskaya, PhD thesis, MIT, 2002.
- ^ Rivest, R.; A. Shamir; L. Adleman (1978). "A Method for Obtaining Digital Signatures and Public-Key Cryptosystems". Communications of the ACM 21 (2): 120–126. doi:10.1145/359340.359342. http://theory.lcs.mit.edu/~rivest/rsapaper.pdf.
- ^ For example any integer r "signs" m=re and the product s1s2 of any two valid signatures s1, s2 of m1, m2 is a valid signature of the product m1m2.
- ^ "Constructing digital signatures from a one-way function.", Leslie Lamport, Technical Report CSL-98, SRI International, Oct. 1979.
- ^ "A certified digital signature", Ralph Merkle, In Gilles Brassard, ed., Advances in Cryptology – CRYPTO '89, vol. 435 of Lecture Notes in Computer Science, pp. 218–238, Spring Verlag, 1990.
- ^ "Digitalized signatures as intractable as factorization." Michael O. Rabin, Technical Report MIT/LCS/TR-212, MIT Laboratory for Computer Science, Jan. 1979
- ^ a b c d "A digital signature scheme secure against adaptive chosen-message attacks.", Shafi Goldwasser, Silvio Micali, and Ronald Rivest. SIAM Journal on Computing, 17(2):281–308, Apr. 1988.
- ^ "Modern Cryptography: Theory & Practice", Wenbo Mao, Prentice Hall Professional Technical Reference, New Jersey, 2004, pg. 308. ISBN 0-13-066943-1
- ^ A. Jøsang, D. Povey and A. Ho. "What You See is Not Always What You Sign". Proceedings of the Australian Unix User Group Symposium (AUUG2002), Melbourne, September 2002. PDF
Books
- J. Katz and Y. Lindell, "Introduction to Modern Cryptography" (Chapman & Hall/CRC Press, 2007)
For books in English on electronic signatures, see:
- Jeremiah S. Buckley, John P. Kromer, Margo H. K. Tank, and R. David Whitaker, The Law of Electronic Signatures (3rd Edition, West Publishing, 2010);
- Lorna Brazell, Electronic Signatures and Identities Law and Regulation (2nd edn, London: Sweet & Maxwell, 2008);
- Stephen Mason, Electronic Signatures in Law (2nd edition, Tottel, 2007);
- Dennis Campbell, editor, E-Commerce and the Law of Digital Signatures (Oceana Publications, 2005);
- M. H. M Schellenkens, Electronic Signatures Authentication Technology from a Legal Perspective, (TMC Asser Press, 2004).
For translations of electronic signature cases from Europe, Brazil, China and Colombia into English, see the Digital Evidence and Electronic Signature Law Review.
Public-key cryptography Algorithms Benaloh · Blum–Goldwasser · Cayley–Purser · CEILIDH · Cramer–Shoup · Damgård–Jurik · DH · DSA · EPOC · ECDH · ECDSA · EKE · ElGamal (encryption · signature scheme) · GMR · Goldwasser–Micali · HFE · IES · Lamport · McEliece · Merkle–Hellman · MQV · Naccache–Stern · NTRUEncrypt · NTRUSign · Paillier · Rabin · RSA · Okamoto–Uchiyama · Schnorr · Schmidt–Samoa · SPEKE · SRP · STS · Three-pass protocol · XTR
Theory Standardization ANS X9F1 · CRYPTREC · IEEE P1363 · NESSIE · NSA Suite B
Topics Digital signature · OAEP · Fingerprint · PKI · Web of trust · Key size
Cryptography Categories:- Asymmetric-key cryptosystems
- Cryptography
- Electronic documents
- Key management
- Public-key cryptography
- Notary
Wikimedia Foundation. 2010.