- Diffie–Hellman key exchange
-
Diffie–Hellman key exchange (D–H)[nb 1] is a specific method of exchanging keys. It is one of the earliest practical examples of key exchange implemented within the field of cryptography. The Diffie–Hellman key exchange method allows two parties that have no prior knowledge of each other to jointly establish a shared secret key over an insecure communications channel. This key can then be used to encrypt subsequent communications using a symmetric key cipher.
The scheme was first published by Whitfield Diffie and Martin Hellman in 1976, although it later emerged that it had been separately invented a few years earlier within GCHQ, the British signals intelligence agency, by Malcolm J. Williamson but was kept classified. In 2002, Hellman suggested the algorithm be called Diffie–Hellman–Merkle key exchange in recognition of Ralph Merkle's contribution to the invention of public-key cryptography (Hellman, 2002).
Although Diffie–Hellman key agreement itself is an anonymous (non-authenticated) key-agreement protocol, it provides the basis for a variety of authenticated protocols, and is used to provide perfect forward secrecy in Transport Layer Security's ephemeral modes (referred to as EDH or DHE depending on the cipher suite).
Contents
History of the protocol
The Diffie–Hellman key agreement was invented in 1976 during a collaboration between Whitfield Diffie and Martin Hellman and was the first practical method for establishing a shared secret over an unprotected communications channel. Ralph Merkle's work on public key distribution was an influence. John Gill suggested application of the discrete logarithm problem. It had first been invented by Malcolm Williamson of GCHQ in the UK some years previously, but GCHQ chose not to make it public until 1997, by which time it had no influence on research in academia.
The method was followed shortly afterwards by RSA, another implementation of public key cryptography using asymmetric algorithms.
In 2002, Martin Hellman wrote:
The system...has since become known as Diffie–Hellman key exchange. While that system was first described in a paper by Diffie and me, it is a public key distribution system, a concept developed by Merkle, and hence should be called 'Diffie–Hellman–Merkle key exchange' if names are to be associated with it. I hope this small pulpit might help in that endeavor to recognize Merkle's equal contribution to the invention of public key cryptography. [1]
U.S. Patent 4,200,770, now expired, describes the algorithm and credits Hellman, Diffie, and Merkle as inventors.
Description
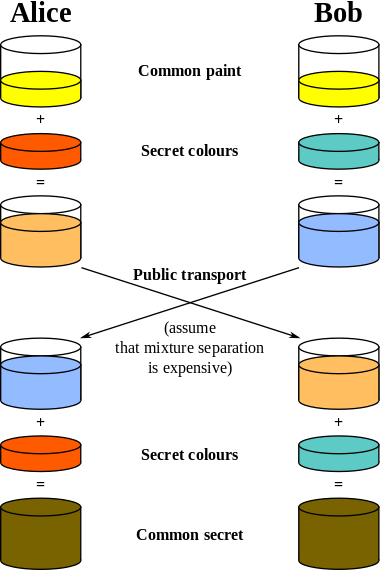
Diffie–Hellman establishes a shared secret that can be used for secret communications by exchanging data over a public network. The following diagram illustrates the general idea of the key exchange:
Here is an explanation which includes the encryption's mathematics:
The simplest, and original, implementation of the protocol uses the multiplicative group of integers modulo p, where p is prime and g is primitive root mod p. Here is an example of the protocol, with non-secret values in green, and secret values in boldface red:Alice Bob Secret Public Calculates Sends Calculates Public Secret a p, g p,g 
b a p, g, A ga mod p = A A 
p, g b a p, g, A  B
Bgb mod p = B p, g, A, B b a, s p, g, A, B Ba mod p = s Ab mod p = s p, g, A, B b, s - Alice and Bob agree to use a prime number p=23 and base g=5.
- Alice chooses a secret integer a=6, then sends Bob A = ga mod p
- A = 56 mod 23
- A = 15,625 mod 23
- A = 8
- Bob chooses a secret integer b=15, then sends Alice B = gb mod p
- B = 515 mod 23
- B = 30,517,578,125 mod 23
- B = 19
- Alice computes s = B a mod p
- s = 196 mod 23
- s = 47,045,881 mod 23
- s = 2
- Bob computes s = A b mod p
- s = 815 mod 23
- s = 35,184,372,088,832 mod 23
- s = 2
- Alice and Bob now share a secret: s = 2. This is because 6*15 is the same as 15*6. So somebody who had known both these private integers might also have calculated s as follows:
- s = 56*15 mod 23
- s = 515*6 mod 23
- s = 590 mod 23
- s = 807,793,566,946,316,088,741,610,050,849,573,099,185,363,389,551,639,556,884,765,625 mod 23
- s = 2
Both Alice and Bob have arrived at the same value, because (ga)b and (gb)a are equal mod p. Note that only a, b and gab = gba mod p are kept secret. All the other values – p, g, ga mod p, and gb mod p – are sent in the clear. Once Alice and Bob compute the shared secret they can use it as an encryption key, known only to them, for sending messages across the same open communications channel. Of course, much larger values of a, b, and p would be needed to make this example secure, since it is easy to try all the possible values of gab mod 23. There are only 23 possible integers as the result of mod 23. If p were a prime of at least 300 digits, and a and b were at least 100 digits long, then even the best algorithms known today could not find a given only g, p, gb mod p and ga mod p, even using all of mankind's computing power. The problem is known as the discrete logarithm problem. Note that g need not be large at all, and in practice is usually either 2 or 5.
Here's a more general description of the protocol:
- Alice and Bob agree on a finite cyclic group G and a generating element g in G. (This is usually done long before the rest of the protocol; g is assumed to be known by all attackers.) We will write the group G multiplicatively.
- Alice picks a random natural number a and sends ga to Bob.
- Bob picks a random natural number b and sends gb to Alice.
- Alice computes (gb)a.
- Bob computes (ga)b.
Both Alice and Bob are now in possession of the group element gab, which can serve as the shared secret key. The values of (gb)a and (ga)b are the same because groups are power associative. (See also exponentiation.)
In order to decrypt a message m, sent as mgab, Bob (or Alice) must first compute (gab)-1, as follows:
Bob knows |G|, b, and ga. A result from group theory establishes that from the construction of G, x|G| = 1 for all x in G.
Bob then calculates (ga)|G|-b = ga(|G|-b) = ga|G|-ab = ga|G|g-ab = (g|G|)ag-ab=1ag-ab=g-ab=(gab)-1.
When Alice sends Bob the encrypted message, mgab, Bob applies (gab)-1 and recovers mgab(gab)-1 = m(1) = m.
Chart
Here is a chart to help simplify who knows what. (Eve is an eavesdropper—she watches what is sent between Alice and Bob, but she does not alter the contents of their communications.)
- Let s = shared secret key. s = 2
- Let g = public base. g = 5
- Let p = public (prime) number. p = 23
- Let a = Alice's private key. a = 6
- Let A = Alice's public key. A = ga mod p = 8
- Let b = Bob's private key. b = 15
- Let B = Bob's public key. B = gb mod p = 19
Alice knows doesn't know p = 23 b = ? base g = 5 a = 6 A = 56 mod 23 = 8 B = 5b mod 23 = 19 s = 196 mod 23 = 2 s = 8b mod 23 = 2 s = 196 mod 23 = 8b mod 23 s = 2 Bob knows doesn't know p = 23 a = ? base g = 5 b = 15 B = 515 mod 23 = 19 A = 5a mod 23 = 8 s = 815 mod 23 = 2 s = 19a mod 23 = 2 s = 815 mod 23 = 19a mod 23 s = 2 Eve knows doesn't know p = 23 a = ? base g = 5 b = ? s = ? A = 5a mod 23 = 8 B = 5b mod 23 = 19 s = 19a mod 23 s = 8b mod 23 s = 19a mod 23 = 8b mod 23 Note: It should be difficult for Alice to solve for Bob's private key or for Bob to solve for Alice's private key. If it is not difficult for Alice to solve for Bob's private key (or vice versa), Eve may simply substitute her own private / public key pair, plug Bob's public key into her private key, produce a fake shared secret key, and solve for Bob's private key (and use that to solve for the shared secret key. Eve may attempt to choose a public / private key pair that will make it easy for her to solve for Bob's private key). A demonstration of Diffie-Hellman (using numbers too small for practical use) is given here
Operation with more than two parties
Diffie-Hellman key agreement is not limited to negotiating a key shared by only two participants. Any number of users can take part in an agreement by performing iterations of the agreement protocol and exchanging intermediate data (which does not itself need to be kept secret). For example, Alice, Bob, and Carol could participate in a Diffie-Hellman agreement as follows, with all operations taken to be modulo p:
- The parties agree on the algorithm parameters p and g.
- The parties generate their private keys, named a, b, and c.
- Alice computes ga and sends it to Bob.
- Bob computes (ga)b = gab and sends it to Carol.
- Carol computes (gab)c = gabc and uses it as her secret.
- Bob computes gb and sends it to Carol.
- Carol computes (gb)c = gbc and sends it to Alice.
- Alice computes (gbc)a = gbca = gabc and uses it as her secret.
- Carol computes gc and sends it to Alice.
- Alice computes (gc)a = gca and sends it to Bob.
- Bob computes (gca)b = gcab = gabc and uses it as his secret.
An eavesdropper has been able to see ga, gb, gc, gab, gac, and gbc, but cannot use any combination of these to reproduce gabc.
To extend this mechanism to larger groups, two basic principles must be followed:
- Starting with an “empty” key consisting only of g, the secret is made by raising the current value to every participant’s private exponent once, in any order (the first such exponentiation yields the participant’s own public key).
- Any intermediate value (having up to N − 1 exponents applied, where N is the number of participants in the group) may be revealed publicly, but the final value (having had all N exponents applied) constitutes the shared secret and hence must never be revealed publicly. Thus, each user must obtain their copy of the secret by applying their own private key last (otherwise there would be no way for the last contributor to communicate the final key to its recipient, as that last contributor would have turned the key into the very secret the group wished to protect).
These principles leave open various options for choosing in which order participants contribute to keys. The simplest and most obvious solution is to arrange the N participants in a circle and have N keys rotate around the circle, until eventually every key has been contributed to by all N participants (ending with its owner) and each participant has contributed to N keys (ending with their own). However, this requires that every participant perform N modular exponentiations.
By choosing a more optimal order, and relying on the fact that keys can be duplicated, it is possible to reduce the number of modular exponentiations performed by each participant to log 2N + 1 using a divide-and-conquer-style approach, given here for eight participants:
- Participants A, B, C, and D each perform one exponentiation, yielding gabcd; this value is sent to E, F, G, and H. In return, participants A, B, C, and D receive gefgh.
- Participants A and B each perform one exponentiation, yielding gefghab, which they send to C and D, while C and D do the same, yielding gefghcd, which they send to A and B.
- Participant A performs an exponentiation, yielding gefghcda, which it sends to B; similarly, B sends gefghcdb to A. C and D do similarly.
- Participant A performs one final exponentiation, yielding the secret gefghcdba = gabcdefgh, while B does the same to get gefghcdab = gabcdefgh; again, C and D do similarly.
- Participants E through H simultaneously perform the same operations using gabcd as their starting point.
Upon completing this algorithm, all participants will possess the secret gabcdefgh, but each participant will have performed only four modular exponentiations, rather than the eight implied by a simple circular arrangement.
Security
The protocol is considered secure against eavesdroppers if G and g are chosen properly. The eavesdropper ("Eve") would have to solve the Diffie–Hellman problem to obtain gab. This is currently considered difficult. An efficient algorithm to solve the discrete logarithm problem would make it easy to compute a or b and solve the Diffie–Hellman problem, making this and many other public key cryptosystems insecure.
The order of G should be prime or have a large prime factor to prevent use of the Pohlig–Hellman algorithm to obtain a or b. For this reason, a Sophie Germain prime q is sometimes used to calculate p=2q+1, called a safe prime, since the order of G is then only divisible by 2 and q. g is then sometimes chosen to generate the order q subgroup of G, rather than G, so that the Legendre symbol of ga never reveals the low order bit of a.
If Alice and Bob use random number generators whose outputs are not completely random and can be predicted to some extent, then Eve's task is much easier.
The secret integers a and b are discarded at the end of the session. Therefore, Diffie–Hellman key exchange by itself trivially achieves perfect forward secrecy because no long-term private keying material exists to be disclosed.
In the original description, the Diffie–Hellman exchange by itself does not provide authentication of the communicating parties and is thus vulnerable to a man-in-the-middle attack. A person in the middle may establish two distinct Diffie–Hellman key exchanges, one with Alice and the other with Bob, effectively masquerading as Alice to Bob, and vice versa, allowing the attacker to decrypt (and read or store) then re-encrypt the messages passed between them. A method to authenticate the communicating parties to each other is generally needed to prevent this type of attack. Variants of Diffie-Hellman, such as STS, may be used instead to avoid these types of attacks.
Other uses
Password-authenticated key agreement
When Alice and Bob share a password, they may use a password-authenticated key agreement (PAKE) form of Diffie–Hellman to prevent man-in-the-middle attacks. One simple scheme is to make the generator g the password. A feature of these schemes is that an attacker can only test one specific password on each iteration with the other party, and so the system provides good security with relatively weak passwords. This approach is described in ITU-T Recommendation X.1035, which is used by the G.hn home networking standard.
Public Key
It is also possible to use Diffie–Hellman as part of a public key infrastructure. Alice's public key is simply (gamod p,g,p). To send her a message Bob chooses a random b, and then sends Alice gbmod p (un-encrypted) together with the message encrypted with symmetric key (ga)bmod p. Only Alice can decrypt the message because only she has a. A preshared public key also prevents man-in-the-middle attacks.
In practice, Diffie–Hellman is not used in this way, with RSA being the dominant public key algorithm. This is largely for historical and commercial reasons, namely that RSA created a Certificate Authority that became Verisign. Diffie–Hellman cannot be used to sign certificates, although the ElGamal and DSA signature algorithms are related to it. However, it is related to MQV, STS and the IKE component of the IPsec protocol suite for securing Internet Protocol communications.
See also
- Key exchange
- Cryptography portal
- Modular arithmetic
- Elliptic curve Diffie–Hellman
- Public-key cryptography
- ElGamal encryption
- Diffie–Hellman problem
- MQV
- Password-authenticated key agreement
- Secure Remote Password Protocol
Notes
- ^ Synonyms of Diffie–Hellman key exchange include:
- Diffie–Hellman key agreement
- Diffie–Hellman key establishment
- Diffie–Hellman key negotiation
- Exponential key exchange
- Diffie–Hellman protocol
- Diffie–Hellman handshake
References
- Dieter Gollmann (2006). Computer Security Second Edition West Sussex, England: John Wiley & Sons, Ltd.
- The possibility of Non-Secret digital encryption J. H. Ellis, January 1970.
- Non-Secret Encryption Using a Finite Field MJ Williamson, January 21, 1974.
- Thoughts on Cheaper Non-Secret Encryption MJ Williamson, August 10, 1976.
- New Directions in Cryptography W. Diffie and M. E. Hellman, IEEE Transactions on Information Theory, vol. IT-22, Nov. 1976, pp: 644–654.
- Cryptographic apparatus and method Martin E. Hellman, Bailey W. Diffie, and Ralph C. Merkle, U.S. Patent #4,200,770, 29 April 1980
- The History of Non-Secret Encryption JH Ellis 1987 (28K PDF file) (HTML version)
- The First Ten Years of Public-Key Cryptography Whitfield Diffie, Proceedings of the IEEE, vol. 76, no. 5, May 1988, pp: 560–577 (1.9MB PDF file)
- Menezes, Alfred; van Oorschot, Paul; Vanstone, Scott (1997). Handbook of Applied Cryptography Boca Raton, Florida: CRC Press. ISBN 0-8493-8523-7. (Available online)
- Singh, Simon (1999) The Code Book: the evolution of secrecy from Mary Queen of Scots to quantum cryptography New York: Doubleday ISBN 0-385-49531-5
- An Overview of Public Key Cryptography Martin E. Hellman, IEEE Communications Magazine, May 2002, pp:42–49. (123kB PDF file)
External links
- Oral history interview with Martin Hellman, Charles Babbage Institute, University of Minnesota. Leading cryptography scholar Martin Hellman discusses the circumstances and fundamental insights of his invention of public key cryptography with collaborators Whitfield Diffie and Ralph Merkle at Stanford University in the mid-1970s.
- RFC 2631 – Diffie–Hellman Key Agreement Method E. Rescorla June 1999.
- Summary of ANSI X9.42: Agreement of Symmetric Keys Using Discrete Logarithm Cryptography[dead link] (64K PDF file) (Description of ANSI 9 Standards)
- Diffie–Hellman Key Exchange – A Non-Mathematician’s Explanation by Keith Palmgren
- Crypt::DH Perl module from CPAN
- Hands-on Diffie–Hellman demonstration
- C implementation using GNU Multiple Precision Arithmetic Library[dead link]
- Diffie Hellman in 2 lines of Perl (using dc)
- Smart Account Management (SAcct) (using DH key exchange to derive session key)
- Talk by Martin Hellman in 2007, Google video
Public-key cryptography Algorithms Benaloh · Blum–Goldwasser · Cayley–Purser · CEILIDH · Cramer–Shoup · Damgård–Jurik · DH · DSA · EPOC · ECDH · ECDSA · EKE · ElGamal (encryption · signature scheme) · GMR · Goldwasser–Micali · HFE · IES · Lamport · McEliece · Merkle–Hellman · MQV · Naccache–Stern · NTRUEncrypt · NTRUSign · Paillier · Rabin · RSA · Okamoto–Uchiyama · Schnorr · Schmidt–Samoa · SPEKE · SRP · STS · Three-pass protocol · XTR
Theory Standardization ANS X9F1 · CRYPTREC · IEEE P1363 · NESSIE · NSA Suite B
Topics Digital signature · OAEP · Fingerprint · PKI · Web of trust · Key size
Cryptography Categories:- Cryptographic protocols
- Asymmetric-key cryptosystems
Wikimedia Foundation. 2010.