- Merkle–Damgård construction
-
In cryptography, the Merkle–Damgård construction or Merkle–Damgård hash function is a method to build collision-resistant cryptographic hash functions from collision-resistant one-way compression functions.[1]:145 This construction was used in the design of many popular hash algorithms such as MD5, SHA1 and SHA2.
The Merkle–Damgård construction was described in Ralph Merkle's Ph.D. thesis in 1979.[2] Ralph Merkle and Ivan Damgård independently proved that the structure is sound: that is, if an appropriate padding scheme is used and the compression function is collision-resistant, then the hash function will also be collision resistant.[3][4]
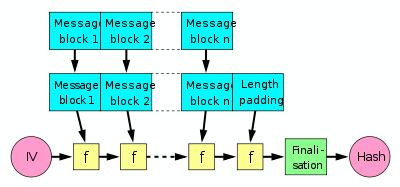
The Merkle–Damgård hash function first applies an MD-compliant padding function to create an output whose size is a multiple of a fixed number (e.g. 512 or 1024) — this is because compression functions cannot handle inputs of arbitrary size. The hash function then breaks the result into blocks of fixed size, and processes them one at a time with the compression function, each time combining a block of the input with the output of the previous round.[1]:146 In order to make the construction secure, Merkle and Damgård proposed that messages be padded with a padding that encodes the length of the original message. This is called length padding or Merkle–Damgård strengthening (see MD-compliant padding).
In the diagram, the one-way compression function is denoted by f, and transforms two fixed length inputs to an output of the same size as one of the inputs. The algorithm starts with an initial value, the initialization vector (IV). The IV is a fixed value (algorithm or implementation specific). For each message block, the compression (or compacting) function f takes the result so far, combines it with the message block, and produces an intermediate result. The last block is padded with zeros as needed and bits representing the length of the entire message are appended. (See below for a detailed length padding example.)
To harden the hash further the last result is then sometimes fed through a finalisation function. The finalisation function can have several purposes such as compressing a bigger internal state (the last result) into a smaller output hash size or to guarantee a better mixing and avalanche effect on the bits in the hash sum. The finalisation function is often built by using the compression function[citation needed] (Note that in some documents instead the act of length padding is called "finalisation".).
Contents
Security characteristics
The popularity of this construction is due to the fact, proven by Merkle and Damgård, that if the one-way compression function f is collision resistant, then so is the hash function constructed using it. Unfortunately, this construction also has several undesirable properties:
- Length extension — once an attacker has one collision, he can find more very cheaply.
- Second preimage attacks against long messages are always much more efficient than brute force.
- Multicollisions (many messages with the same hash) can be found with only a little more work than collisions.[5]
- "Herding attacks" (first committing to an output h, then mapping messages with arbitrary starting values to h) are possible for more work than finding a collision, but much less than would be expected to do this for a random oracle.[6]
- "Extension attacks": Given the hash H(X) of an unknown input X, it is easy to find the value of H(pad(X) || Y), where pad is the padding function of the hash. That is, it is possible to find hashes of inputs related to X even though X remains unknown.[7] A random oracle would not have this property, and this may lead to simple attacks even for natural schemes proven secure in the random oracle model.[8]
Wide pipe construction
Due to several structural weaknesses of Merkle–Damgård construction, especially the length extension problem and multicollision attacks, Stefan Lucks proposed the use of the wide-pipe hash[9] instead of Merkle–Damgård construction. The wide-pipe hash is very similar to the Merkle–Damgård construction but has a larger internal state size, meaning that the bit-length that is internally used is larger than the output bit-length. If a hash of n bit is desired, the compression function f takes 2n bit of chaining falue and m bit of the message and compresses this to an output of 2n bit.
Therefore, in final step a second compression function compresses the last internal hash value (2n bit) to the final hash value (n bit). This can be done as simple as to discard half of the last 2n-bit-output. SHA-224 and SHA-384 take this form since they are derived from SHA-256 and SHA-512, respectively.
Fast wide pipe construction
It has been demonstrated by Mridul Nandi and Souradyuti Paul that the Widepipe hash function can be made approximately twice faster, if the widepipe state can be divided in half in the following manner: one half is inputted to the succeeding compression function when the other half is combined with the output of that compression function.[10]
The main idea of the hash construction is to feed-forward half of the previous chaining value to XOR it to the output of the compression function. In so doing the construction takes in longer messageblock every iteration than original widepipe. Using the same function f as before, it takes n bit chaining value and n+m bit of the message. However, the price to pay is the extra memory used in the construction for feed-forward.
MD-compliant padding
As mentioned in the introduction, the padding scheme used in the Merkle–Damgård construction must be chosen carefully to ensure the security of the scheme. Mihir Bellare gives sufficient conditions for a padding scheme to possess to ensure that the MD construction is secure: the scheme must be "MD-compliant" (the original length-padding scheme used by Merkle is an example of MD-compliant padding).[1]:145 Conditions:
- M is a prefix of

- If | M1 | = | M2 | then

- If
 then the last block of
then the last block of  is different from the last block of
is different from the last block of 
With these conditions in place, we find a collision in the MD hash function exactly when we find a collision in the underlying compression function. Therefore, the Merkle–Damgård construction is provably secure when the underlying compression function is secure.[1]:147
Length padding example
To be able to feed the message to the compression function, the last block needs to be padded with constant data (generally with zeroes) to a full block.
- For example, let's say the message to be hashed is "HashInput" and the block size of the compression function is 8 bytes (64 bits). So we get two blocks looking like this:
- HashInpu t0000000
But this is not enough since it would mean that distinct messages starting by the same data and terminated by zero or more bytes from the padding constant data would get fed into the reduction function using exactly the same blocks, producing the same final hash sum.
- In our example, for instance, the modified message "HashInput00" would generate the same blocks as the original message "HashInput".
To prevent this, the first bit of the padded constant data must be changed. As the constant padding is generally made of zeroes, the first padding bit will be mandatorily changed into "1".
- In our example, we get something like this:
- HashInpu t1000000
To harden the hash even further also, the length of the message can be added in an extra block.
- So in our example, we would get three blocks like this:
- HashInpu t1000000 00000009
To avoid ambiguity, the message length value must be itself resistant to length extensions. Most common implementations use a fixed bit-size (generally 64 or 128 bits in modern algorithms) and a fixed position at end of the last block for encoding the message length value.
Now that is a bit wasteful since it means hashing one full extra block for the length value. So there is a slight speed optimisation that most hash algorithms use. If there is space enough among the zeros padded to the last block the length value can instead be padded there.
- Let's say here that, in our example the length value is encoded on 5 bytes (40 bits), thus it gets padded in the final block as "00009", not just "9" or with too many unnecessary zeroes. Like this:
- HashInpu t1000009
References
- Handbook of Applied Cryptography by Menezes, van Oorschot and Vanstone (2001), chapter 9.
- Introduction to Modern Cryptography, by Jonathan Katz and Yehuda Lindell. Chapman and Hall/CRC Press, August 2007, page 134 (construction 4.13).
- ^ a b c d Goldwasser, S. and Bellare, M. "Lecture Notes on Cryptography". Summer course on cryptography, MIT, 1996-2001
- ^ R.C. Merkle. Secrecy, authentication, and public key systems. Stanford Ph.D. thesis 1979, pages 13-15.
- ^ R.C. Merkle. A Certified Digital Signature. In Advances in Cryptology - CRYPTO '89 Proceedings, Lecture Notes in Computer Science Vol. 435, G. Brassard, ed, Springer-Verlag, 1989, pp. 218-238.
- ^ I. Damgård. A Design Principle for Hash Functions. In Advances in Cryptology - CRYPTO '89 Proceedings, Lecture Notes in Computer Science Vol. 435, G. Brassard, ed, Springer-Verlag, 1989, pp. 416-427.
- ^ Antoine Joux. Multicollisions in iterated hash functions. Application to cascaded construction. In Advances in Cryptology - CRYPTO '04 Proceedings, Lecture Notes in Computer Science, Vol. 3152, M. Franklin, ed, Springer-Verlag, 2004, pp. 306–316.
- ^ John Kelsey and Tadayoshi Kohno. Herding Hash Functions and the Nostradamus Attack In Eurocrypt 2006, Lecture Notes in Computer Science, Vol. 4004, pp. 183–200.
- ^ Yevgeniy Dodis, Thomas Ristenpart, Thomas Shrimpton. Salvaging Merkle–Damgård for Practical Applications. Preliminary version in Advances in Cryptology - EUROCRYPT '09 Proceedings, Lecture Notes in Computer Science Vol. 5479, A. Joux, ed, Springer-Verlag, 2009, pp. 371–388.
- ^ J.S. Coron, Y. Dodis, C. Malinaud, and P. Puniya. Merkle–Damgård Revisited: How to Construct a Hash Function. Advances in Cryptology – CRYPTO '05 Proceedings, Lecture Notes in Computer Science, Vol. 3621, Springer-Verlag, 2005, pp. 21–39.
- ^ S. Lucks, Design Principles for Iterated Hash Functions, In: Cryptology ePrint Archive, Report 2004/253, 2004.
- ^ Mridul Nandi and Souradyuti Paul. Speeding Up the Widepipe: Secure and Fast Hashing. In Guang Gong and Kishan Gupta, editor, Indocrypt 2010, Springer, 2010.
Cryptographic hash functions and message authentication codes (MACs) Common functions Functions SHA-3 finalists BLAKE · Grøstl · JH · Keccak · SkeinMAC algorithms Authenticated
encryption modesAttacks Misc. Standardization Cryptography Categories:- Cryptographic hash functions
Wikimedia Foundation. 2010.