- Logic gate
-
A logic gate is an idealized or physical device implementing a Boolean function, that is, it performs a logical operation on one or more logic inputs and produces a single logic output. Depending on the context, the term may refer to an ideal logic gate, one that has for instance zero rise time and unlimited fan-out, or it may refer to a non-ideal physical device.[1] (see Ideal and real op-amps for comparison)
Logic gates are primarily implemented using diodes or transistors acting as electronic switches, but can also be constructed using electromagnetic relays (relay logic), fluidic logic, pneumatic logic, optics, molecules, or even mechanical elements. With amplification, logic gates can be cascaded in the same way that Boolean functions can be composed, allowing the construction of a physical model of all of Boolean logic, and therefore, all of the algorithms and mathematics that can be described with Boolean logic.
Contents
Background
The simplest form of electronic logic is diode logic. This allows AND and OR gates to be built, but not inverters, and so is an incomplete form of logic. Further, without some kind of amplification it is not possible to have such basic logic operations cascaded as required for more complex logic functions. To build a functionally complete logic system, relays, valves (vacuum tubes), or transistors can be used. The simplest family of logic gates using bipolar transistors is called resistor-transistor logic (RTL). Unlike diode logic gates, RTL gates can be cascaded indefinitely to produce more complex logic functions. These gates were used in early integrated circuits. For higher speed, the resistors used in RTL were replaced by diodes, leading to diode-transistor logic (DTL). Transistor-transistor logic (TTL) then supplanted DTL with the observation that one transistor could do the job of two diodes even more quickly, using only half the space. In virtually every type of contemporary chip implementation of digital systems, the bipolar transistors have been replaced by complementary field-effect transistors (MOSFETs) to reduce size and power consumption still further, thereby resulting in complementary metal–oxide–semiconductor (CMOS) logic.
For small-scale logic, designers now use prefabricated logic gates from families of devices such as the TTL 7400 series by Texas Instruments and the CMOS 4000 series by RCA, and their more recent descendants. Increasingly, these fixed-function logic gates are being replaced by programmable logic devices, which allow designers to pack a large number of mixed logic gates into a single integrated circuit. The field-programmable nature of programmable logic devices such as FPGAs has removed the 'hard' property of hardware; it is now possible to change the logic design of a hardware system by reprogramming some of its components, thus allowing the features or function of a hardware implementation of a logic system to be changed.
Electronic logic gates differ significantly from their relay-and-switch equivalents. They are much faster, consume much less power, and are much smaller (all by a factor of a million or more in most cases). Also, there is a fundamental structural difference. The switch circuit creates a continuous metallic path for current to flow (in either direction) between its input and its output. The semiconductor logic gate, on the other hand, acts as a high-gain voltage amplifier, which sinks a tiny current at its input and produces a low-impedance voltage at its output. It is not possible for current to flow between the output and the input of a semiconductor logic gate.
Another important advantage of standardized integrated circuit logic families, such as the 7400 and 4000 families, is that they can be cascaded. This means that the output of one gate can be wired to the inputs of one or several other gates, and so on. Systems with varying degrees of complexity can be built without great concern of the designer for the internal workings of the gates, provided the limitations of each integrated circuit are considered.
The output of one gate can only drive a finite number of inputs to other gates, a number called the 'fanout limit'. Also, there is always a delay, called the 'propagation delay', from a change in input of a gate to the corresponding change in its output. When gates are cascaded, the total propagation delay is approximately the sum of the individual delays, an effect which can become a problem in high-speed circuits. Additional delay can be caused when a large number of inputs are connected to an output, due to the distributed capacitance of all the inputs and wiring and the finite amount of current that each output can provide.
Logic gates
All other types of Boolean logic gates (i.e., AND, OR, NOT, XOR, XNOR) can be created from a suitable network of NAND gates. Similarly all gates can be created from a network of NOR gates. Historically, NAND gates were easier to construct from MOS technology and thus NAND gates served as the first pillar of Boolean logic in electronic computation.
For an input of 2 boolean variables, there are 16 possible boolean algebraic functions. These 16 functions are enumerated below, together with their outputs for each combination of input variables.
INPUT A 0 0 1 1 Meaning B 0 1 0 1 OUTPUT FALSE 0 0 0 0 Whatever A and B, the output is false. Contradiction. A AND B 0 0 0 1 Output is true if and only if (iff) both A and B are true. A  B
B0 0 1 0 A doesn't imply B. True if A but not B. A 0 0 1 1 True whenever A is true. A  B
B0 1 0 0 A is not implied by B. True if not A but B. B 0 1 0 1 True whenever B is true. A XOR B 0 1 1 0 True if A is not equal to B. A OR B 0 1 1 1 True if A is true, or B is true, or both. A NOR B 1 0 0 0 True if neither A nor B. A XNOR B 1 0 0 1 True if A is equal to B. NOT B 1 0 1 0 True if B is false. A  B
B1 0 1 1 A is implied by B. False if not A but B, otherwise true. NOT A 1 1 0 0 True if A is false. A  B
B1 1 0 1 A implies B. False if A but not B, otherwise true. A NAND B 1 1 1 0 A and B are not both true. TRUE 1 1 1 1 Whatever A and B, the output is true. Tautology. The four functions denoted by arrows are the logical implication functions. These functions are not usually implemented as elementary circuits, but rather as combinations of a gate with an inverter at one input.
Symbols
There are two sets of symbols for elementary logic gates in common use, both defined in ANSI/IEEE Std 91-1984 and its supplement ANSI/IEEE Std 91a-1991. The "distinctive shape" set, based on traditional schematics, is used for simple drawings, and derives from MIL-STD-806 of the 1950s and 1960s. It is sometimes unofficially described as "military", reflecting its origin. The "rectangular shape" set, based on IEC 60617-12 and other early industry standards, has rectangular outlines for all types of gate, and allows representation of a much wider range of devices than is possible with the traditional symbols. The IEC's system has been adopted by other standards, such as EN 60617-12:1999 in Europe and BS EN 60617-12:1999 in the United Kingdom.
The goal of IEEE Std 91-1984 was to provide a uniform method of describing the complex logic functions of digital circuits with schematic symbols. These functions were more complex than simple AND and OR gates. They could be medium scale circuits such as a 4-bit counter to a large scale circuits such as a microprocessor. IEC 617-12 and its successor IEC 60617-12 do not explicitly show the "distinctive shape" symbols, but do not prohibit them. [1] These are, however, shown in ANSI/IEEE 91 (and 91a) with this note: "The distinctive-shape symbol is, according to IEC Publication 617, Part 12, not preferred, but is not considered to be in contradiction to that standard." This compromise was reached between the respective IEEE and IEC working groups to permit the IEEE and IEC standards to be in mutual compliance with one another.
In the 1980s, schematics were the predominant method to design both circuit boards and custom ICs known as gate arrays. Today custom ICs and the field-programmable gate array are typically designed with Hardware Description Languages (HDL) such as Verilog or VHDL.
Type Distinctive shape Rectangular shape Boolean algebra between A & B Truth table AND 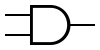


INPUT OUTPUT A B A AND B 0 0 0 0 1 0 1 0 0 1 1 1 OR 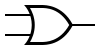

A + B INPUT OUTPUT A B A OR B 0 0 0 0 1 1 1 0 1 1 1 1 NOT 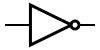

INPUT OUTPUT A NOT A 0 1 1 0 In electronics a NOT gate is more commonly called an inverter. The circle on the symbol is called a bubble, and is used in logic diagrams to indicate a logic negation between the external logic state and the internal logic state (1 to 0 or vice versa). On a circuit diagram it must be accompanied by a statement asserting that the positive logic convention or negative logic convention is being used (high voltage level = 1 or high voltage level = 0, respectively). The wedge is used in circuit diagrams to directly indicate an active-low (high voltage level = 0) input or output without requiring a uniform convention throughout the circuit diagram. This is called Direct Polarity Indication. See IEEE Std 91/91A and IEC 60617-12. Both the bubble and the wedge can be used on distinctive-shape and rectangular-shape symbols on circuit diagrams, depending on the logic convention used. On pure logic diagrams, only the bubble is meaningful. NAND 


INPUT OUTPUT A B A NAND B 0 0 1 0 1 1 1 0 1 1 1 0 NOR 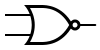


INPUT OUTPUT A B A NOR B 0 0 1 0 1 0 1 0 0 1 1 0 XOR 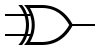


INPUT OUTPUT A B A XOR B 0 0 0 0 1 1 1 0 1 1 1 0 XNOR 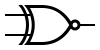

 or
or 
INPUT OUTPUT A B A XNOR B 0 0 1 0 1 0 1 0 0 1 1 1 Two more gates are the exclusive-OR or XOR function and its inverse, exclusive-NOR or XNOR. The two input Exclusive-OR is true only when the two input values are different, false if they are equal, regardless of the value. If there are more than two inputs, the gate generates a true at its output if the number of trues at its input is odd ([2]). In practice, these gates are built from combinations of simpler logic gates.
Universal logic gates
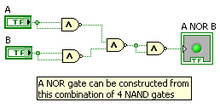
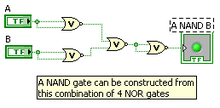
Charles Sanders Peirce (winter of 1880–81) showed that NOR gates alone (or alternatively NAND gates alone) can be used to reproduce the functions of all the other logic gates, but his work on it was unpublished until 1933.[2] The first published proof was by Henry M. Sheffer in 1913, so the NAND logical operation is sometimes called Sheffer stroke; the logical NOR is sometimes called Peirce's arrow.[3] Consequently, these gates are sometimes called universal logic gates.[4]
De Morgan equivalent symbols
By use of De Morgan's theorem, an AND function is identical to an OR function with negated inputs and outputs. Likewise, an OR function is identical to an AND function with negated inputs and outputs. Similarly, a NAND gate is equivalent to an OR gate with negated inputs, and a NOR gate is equivalent to an AND gate with negated inputs.
This leads to an alternative set of symbols for basic gates that use the opposite core symbol (AND or OR) but with the inputs and outputs negated or inverted. Use of these alternative symbols can make logic circuit diagrams much clearer and help to show accidental connection of an active high output to an active low input or vice-versa. Any connection that has logic negations at both ends can be replaced by a negationless connection and a suitable change of gate or vice-versa. Any connection that has a negation at one end and no negation at the other can be made easier to interpret by instead using the De Morgan equivalent symbol at either of the two ends. When negation or polarity indicators on both ends of a connection match, there is no logic negation in that path (effectively, bubbles "cancel"), making it easier to follow logic states from one symbol to the next. This is commonly seen in real logic diagrams - thus the reader must not get into the habit of associating the shapes exclusively as OR or AND shapes, but also take into account the bubbles at both inputs and outputs in order to determine the "true" logic function indicated.
All logic relations can be realized by using NAND gates (this can also be done using NOR gates). De Morgan's theorem is most commonly used to transform all logic gates to NAND gates or NOR gates. This is done mainly since it is easy to buy logic gates in bulk and because many electronics labs stock only NAND and NOR gates.
Data storage
Logic gates can also be used to store data. A storage element can be constructed by connecting several gates in a "latch" circuit. More complicated designs that use clock signals and that change only on a rising or falling edge of the clock are called edge-triggered "flip-flops". The combination of multiple flip-flops in parallel, to store a multiple-bit value, is known as a register. When using any of these gate setups the overall system has memory; it is then called a sequential logic system since its output can be influenced by its previous state(s).
These logic circuits are known as computer memory. They vary in performance, based on factors of speed, complexity, and reliability of storage, and many different types of designs are used based on the application.
Three-state logic gates
Main article: Tri-state bufferThree-state, or 3-state, logic gates are a type of logic gates that have three states of the output: high (H), low (L) and high-impedance (Z). The high-impedance state plays no role in the logic, which remains strictly binary. These devices are used on buses also known as the Data Buses of the CPU to allow multiple chips to send data. A group of three-states driving a line with a suitable control circuit is basically equivalent to a multiplexer, which may be physically distributed over separate devices or plug-in cards.
In electronics, a high output would mean the output is sourcing current from the positive power terminal (positive voltage). A low output would mean the output is sinking current to the negative power terminal (zero voltage). High impedance would mean that the output is effectively disconnected from the circuit.
'Tri-state', a widely-used synonym of 'three-state', is a trademark of the National Semiconductor Corporation.
Miscellaneous
Logic circuits include such devices as multiplexers, registers, arithmetic logic units (ALUs), and computer memory, all the way up through complete microprocessors, which may contain more than 100 million gates. In practice, the gates are made from field-effect transistors (FETs), particularly MOSFETs (metal–oxide–semiconductor field-effect transistors).
Compound logic gates AND-OR-Invert (AOI) and OR-AND-Invert (OAI) are often employed in circuit design because their construction using MOSFET's is simpler and more efficient than the sum of the individual gates.[5]
In reversible logic, Toffoli gates are used.
History and development
In a 1886 letter, Charles Sanders Peirce described how logical operations could be carried out by electrical switching circuits.[6] Starting in 1898, Nikola Tesla filed for patents of devices containing electro-mechanical logic gate circuits (see List of Tesla patents). Eventually, vacuum tubes replaced relays for logic operations. Lee De Forest's modification, in 1907, of the Fleming valve can be used as AND logic gate. Ludwig Wittgenstein introduced a version of the 16-row truth table, which is shown above, as proposition 5.101 of Tractatus Logico-Philosophicus (1921). Claude E. Shannon introduced the use of Boolean algebra in the analysis and design of switching circuits in 1937. Walther Bothe, inventor of the coincidence circuit, got part of the 1954 Nobel Prize in physics, for the first modern electronic AND gate in 1924. Active research is taking place in molecular logic gates.
Implementations
Since the 1990s, most logic gates are made of CMOS transistors (i.e. NMOS and PMOS transistors are used). Often millions of logic gates are packaged in a single integrated circuit.
There are several logic families with different characteristics (power consumption, speed, cost, size) such as: RDL (resistor-diode logic), RTL (resistor-transistor logic), DTL (diode-transistor logic), TTL (transistor-transistor logic) and CMOS (complementary metal oxide semiconductor). There are also sub-variants, e.g. standard CMOS logic vs. advanced types using still CMOS technology, but with some optimizations for avoiding loss of speed due to slower PMOS transistors.
Non-electronic implementations are varied, though few of them are used in practical applications. Many early electromechanical digital computers, such as the Harvard Mark I, were built from relay logic gates, using electro-mechanical relays. Logic gates can be made using pneumatic devices, such as the Sorteberg relay or mechanical logic gates, including on a molecular scale.[7] Logic gates have been made out of DNA (see DNA nanotechnology)[8] and used to create a computer called MAYA (see MAYA II). Logic gates can be made from quantum mechanical effects (though quantum computing usually diverges from boolean design). Photonic logic gates use non-linear optical effects
See also
- And-inverter graph
- Boolean algebra topics
- Boolean function
- Digital circuit
- Espresso heuristic logic minimizer
- Fanout
- Flip-flop (electronics)
- Karnaugh map
- Combinational logic
- Logic family
- Logical graph
- NMOS logic
- Propositional calculus
- Race hazard
- Reversible computing
- Truth table
References
- ^ Jaeger, Microelectronic Circuit Design, McGraw-Hill 1997, ISBN 0-07-032482-4, pp. 226-233
- ^ Peirce, C. S. (manuscript winter of 1880–81), "A Boolean Algebra with One Constant", published 1933 in Collected Papers v. 4, paragraphs 12–20. Reprinted 1989 in Writings of Charles S. Peirce v. 4, pp. 218-21, Google Preview. See Roberts, Don D. (2009), The Existential Graphs of Charles S. Peirce, p. 131.
- ^ Hans Kleine Büning; Theodor Lettmann (1999). Propositional logic: deduction and algorithms. Cambridge University Press. p. 2. ISBN 9780521630177. http://books.google.com/books?id=3oJE9yczr3EC&pg=PA2.
- ^ John Bird (2007). Engineering mathematics. Newnes. p. 532. ISBN 9780750685559. http://books.google.com/books?id=1-fBmsEBNUoC&pg=PA532.
- ^ Tinder, Richard F. (2000). Engineering digital design: Revised Second Edition. pp. 317–319. ISBN 0126912955. http://books.google.com/books?id=6x0pjjMKRh0C&pg=PT347&lpg=PT347&dq=AOI+gate&ct=result#PPT346,M1. Retrieved 2008-07-04.
- ^ Peirce, C. S., "Letter, Peirce to A. Marquand", dated 1886, Writings of Charles S. Peirce, v. 5, 1993, pp. 541–3. Google Preview. See Burks, Arthur W., "Review: Charles S. Peirce, The new elements of mathematics", Bulletin of the American Mathematical Society v. 84, n. 5 (1978), pp. 913–18, see 917. PDF Eprint.
- ^ Mechanical Logic gates (focused on molecular scale)
- ^ DNA Logic gates
Further reading
- Awschalom, D., D. Loss, and N. Samarth, Semiconductor Spintronics and Quantum Computation (2002), Springer-Verlag, Berlin, Germany.
- Bostock, Geoff, Programmable Logic Devices. Technology and Applications (1988), McGraw-Hill, New York, NY.
- Brown, Stephen D. et al., Field-Programmable Gate Arrays (1992), Kluwer Academic Publishers, Boston, MA.
External links
- Digital Logic Simulator v0.4 - Brad-Ware Studios' free program that supports real-time edit and simulation, as well as abstracting. Include entire scenes that you have created, as a single chip.
- Using Logic Gates
- Online logic gate simulator
- Java applet of NOT gate
- LogicCircuit – is free educational software for designing and simulating digital logic circuits.
- Logic Gate Simulator in Adobe Flex
- Redstone circuits on the minecraft wiki (a specific type of simulated logic circuitry).
- Wireless Remote Control and the Electronic Computer Logic Gate, 21st Century Books, Colorado.
Digital systems Components - Logic gate
- Combinational logic
- Sequential logic
- Digital circuit
- Integrated circuit (IC)
Theory Applications Categories:- Logic gates
Wikimedia Foundation. 2010.