Radiocarbon dating

Radiocarbon dating (sometimes simply known as carbon dating) is a radiometric dating method that uses the naturally occurring radioisotope carbon-14 (¹⁴C) to estimate the age of carbon-bearing materials up to about 58,000 to 62,000 years.^[1] Raw, i.e. uncalibrated, radiocarbon ages are usually reported in radiocarbon years "Before Present" (BP), "Present" being defined as 1950. Such raw ages can be calibrated to give calendar dates. One of the most frequent uses of radiocarbon dating is to estimate the age of organic remains from archaeological sites. When plants fix atmospheric carbon dioxide (CO₂) into organic material during photosynthesis they incorporate a quantity of ¹⁴C that approximately matches the level of this isotope in the atmosphere (a small difference occurs because of isotope fractionation, but this is corrected after laboratory analysis^{[citation needed]}). After plants die or they are consumed by other organisms (for example, by humans or other animals) the ¹⁴C fraction of this organic material declines at a fixed exponential rate due to the radioactive decay of ¹⁴C. Comparing the remaining ¹⁴C fraction of a sample to that expected from atmospheric ¹⁴C allows the age of the sample to be estimated.

The technique of radiocarbon dating was developed by Willard Libby and his colleagues at the University of Chicago in 1949. Emilio Segrè asserted in his autobiography that Enrico Fermi suggested the concept to Libby in a seminar at Chicago that year. Libby estimated that the steady state radioactivity concentration of exchangeable carbon-14 would be about 14 disintegrations per minute (dpm) per gram. In 1960, he was awarded the Nobel Prize in chemistry for this work. He demonstrated the accuracy of radiocarbon dating by accurately estimating the age of wood from a series of samples for which the age was known, including an ancient Egyptian royal barge of 1850 BC.^[2][3]

Basic physics

1: Formation of Carbon-14
2: Decay of Carbon-14
3: The equation is for living organisms, and the inequality is for dead organisms, in which the C-14 then decays (See 2).

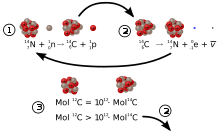
Carbon has two stable, nonradioactive isotopes: carbon-12 (¹²C), and carbon-13 (¹³C). In addition, there are trace amounts of the unstable isotope carbon-14 (¹⁴C) on Earth. Carbon-14 has a relatively short half-life of 5730 years, meaning that the amount of carbon-14 in a sample is halved over the course of 5730 years due to radioactive decay. Carbon-14 would have long ago vanished from Earth were it not for the unremitting cosmic ray flux interactions with the Earth's atmosphere, which create more of the isotope. The neutrons resulting from the cosmic ray interactions participate in the following nuclear reaction on the atoms of nitrogen molecules (N₂) in the atmosphere:

$n + \mathrm{^{14}_{7}N} \rightarrow \mathrm{^{14}_{6}C} + p$

The highest rate of carbon-14 production takes place at altitudes of 9 to 15 km (30,000 to 50,000 ft), and at high geomagnetic latitudes, but the carbon-14 spreads evenly throughout the atmosphere and reacts with oxygen to form carbon dioxide. Carbon dioxide also permeates the oceans, dissolving in the water. For approximate analysis it is assumed that the cosmic ray flux is constant over long periods of time; thus carbon-14 is produced at a constant rate and the proportion of radioactive to non-radioactive carbon is constant: ca. 1 part per trillion (600 billion atoms/mole). In 1958 Hessel de Vries showed that the concentration of carbon-14 in the atmosphere varies with time and locality.^[4] For the most accurate work, these variations are compensated by means of calibration curves. When these curves are used, their accuracy and shape are the factors that determine the accuracy of the age obtained for a given sample.^{[5] 14}C can also be produced at ground level at a rate of 1 x 10⁻⁴ g⁻¹s⁻¹, which is not considered significant enough to impact on dating without a known other source of neutrons.^[6]

Plants take up atmospheric carbon dioxide by photosynthesis, and are ingested by animals, so every living thing is constantly exchanging carbon-14 with its environment as long as it lives. Once it dies, however, this exchange stops, and the amount of carbon-14 gradually decreases through radioactive beta decay with a half-life of 5,730 ± 40 years ^[7]. Carbon-14 is stored in different amounts in different reservoirs because there is a dynamic equilibrium between ¹⁴C production and decay.^[6]

$\mathrm{~^{14}_{6}C}\rightarrow\mathrm{~^{14}_{7}N}+ e^{-} + \bar{\nu}_e$

Carbon-14 was discovered on February 27, 1940, by Martin Kamen and Sam Ruben at the University of California Radiation Laboratory at Berkeley.

Computation of ages and dates

The number of decays per time is proportional to the current number of radioactive atoms. This is expressed by the following differential equation, where N is the number of radioactive atoms and λ is a positive number called the decay constant:

$\frac{dN}{dt} = -\lambda N.$

As the solution to this equation, the number of radioactive atoms N can be written as a function of time

$N(t) = N_0e^{-\lambda t}\,$,

which describes an exponential decay over a timespan t with an initial condition of N₀ radioactive atoms at t = 0. Canonically, t is 0 when the decay started. In this case, N₀ is the initial number of ¹⁴C atoms when the decay started.

For radiocarbon dating a once living organism, the initial ratio of ¹⁴C atoms to the sum of all other carbon atoms at the point of the organism's death and hence the point when the decay started, is approximately the ratio in the atmosphere.

Two characteristic times can be defined:

• mean- or average-life: mean or average time each radiocarbon atom spends in a given sample until it decays.
• half-life: time lapsed for half the number of radiocarbon atoms in a given sample, to decay,

It can be shown that:

$t_{avg} \,$ = $\frac{1}{\lambda}$ = radiocarbon mean- or average-life = 8033 years (Libby value)

$t_\frac{1}{2} \,$ = $t_{avg} \cdot \ln 2$ = radiocarbon half-life = 5568 years (Libby value)

Notice that dates are customarily given in years BP which implies t(BP) = –t because the time arrow for dates runs in reverse direction from the time arrow for the corresponding ages. From these considerations and the above equation, it results:

For a raw radiocarbon date:

$t(BP) = \frac{1}{\lambda} {\ln \frac{N}{N_0}}$

and for a raw radiocarbon age:

$t(BP) = -\frac{1}{\lambda} {\ln \frac{N}{N_0}}$

After replacing values, the raw radiocarbon age becomes any of the following equivalent formulae:

using logs base e and the average life:

$t(BP) = -t_{avg}\cdot \ln{\frac{N}{N_0}}$

and

using logs base 2 and the half-life:

$t(BP) = -t_\frac{1}{2}\cdot \log_2 \frac{N}{N_0}$

Wiggle matching uses the non-linear relationship between the ¹⁴C age and calendar age to match the shape of a series of closely sequentially spaced ¹⁴C dates with the ¹⁴C calibration curve.

Measurements and scales

The use of accelerator mass spectrometers can improve the sensitivity of radiocarbon dating.

Measurements are traditionally made by counting the radioactive decay of individual carbon atoms by gas proportional counting or by liquid scintillation counting. For samples of sufficient size (several grams of carbon) this method is still widely used in the 2000s. Among others, all the tree ring samples used for the calibration curves (see below) were determined by these counting techniques. Such decay counting, however, is relatively insensitive and subject to large statistical uncertainties for small samples. When there is little carbon-14 to begin with, the long radiocarbon half-life means that very few of the carbon-14 atoms will decay during the time allotted for their detection, resulting in few disintegrations per minute.

The sensitivity of the method has been greatly increased by the use of accelerator mass spectrometry (AMS). With this technique ¹⁴C atoms can be detected and counted directly vs only detecting those atoms that decay during the time interval allotted for an analysis. AMS allows dating samples containing only a few milligrams of carbon.

Raw radiocarbon ages (i.e., those not calibrated) are usually reported in "years Before Present" (BP). This is the number of radiocarbon years before 1950, based on a nominal (and assumed constant – see "calibration" below) level of carbon-14 in the atmosphere equal to the 1950 level. These raw dates are also based on a slightly-off historic value for the radiocarbon half-life. Such value is used for consistency with earlier published dates (see "Radiocarbon half-life" below). See the section on computation for the basis of the calculations.

Radiocarbon dating laboratories generally report an uncertainty for each date. For example, 3000 ± 30 BP indicates a standard deviation of 30 radiocarbon years. Traditionally this included only the statistical counting uncertainty. However, some laboratories supplied an "error multiplier" that could be multiplied by the uncertainty to account for other sources of error in the measuring process. More recently, the laboratories try to quote the overall uncertainty, which is determined from control samples of known age and verified by international intercomparison exercises.^[8] In 2008, a typical uncertainty better than ±40 radiocarbon years can be expected for samples younger than 10,000 years. This, however, is only a small part of the uncertainty of the final age determination (see section Calibration below).

Samples older than the upper age-limit cannot be dated because the small number of remaining intrinsic ¹⁴C atoms will be obscured by ¹⁴C background atoms introduced into the samples while they still resided in the environment, during sample preparation, or in the detection instrument. As of 2007^[update], the limiting age for a 1 milligram sample of graphite is about ten half-lives, approximately 60,000 years.^[9] This age is derived from that of the calibration blanks used in an analysis, whose ¹⁴C content is assumed to be the result of contamination during processing (as a result of this, some facilities^[9] will not report an age greater than 60,000 years for any sample).

A variety of sample processing and instrument-based constraints have been postulated to explain the upper age-limit. To examine instrument-based background activities in the AMS instrument of the W. M. Keck Carbon Cycle Accelerator Mass Spectrometry Laboratory of the University of California, a set of natural diamonds were dated. Natural diamond samples from different sources within rock formations with standard geological ages in excess of 100 Ma yielded¹⁴C apparent ages 64,920 ± 430 BP to 80,000 ± 1100 BP as reported in 2007.^[10]

Calibration

The need for calibration

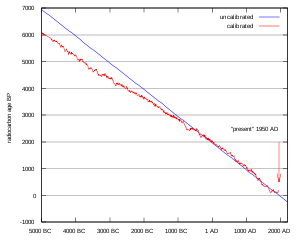Calibration curve for the radiocarbon dating scale. Data sources: Stuiver et al. (1998).^[11] Samples with a real date more recent than AD 1950 are dated and/or tracked using the N- & S-Hemisphere graphs. See following figure.

Atmospheric ¹⁴C, New Zealand^[12] and Austria.^[13] The New Zealand curve is representative for the Southern Hemisphere, the Austrian curve is representative for the Northern Hemisphere. Atmospheric nuclear weapon tests almost doubled the concentration of ¹⁴C in the Northern Hemisphere.^[14]

Dates may be expressed as either uncalibrated or calibrated years. A raw BP date cannot be used directly as a calendar date, because the level of atmospheric ¹⁴C has not been strictly constant during the span of time that can be radiocarbon dated. The level is affected by variations in the cosmic ray intensity which is in turn affected by variations in the Earth's magnetosphere.^[15] In addition, there are substantial reservoirs of carbon in organic matter, the ocean, ocean sediments (see methane hydrate), and sedimentary rocks. Changes in the Earth's climate can affect the carbon flows between these reservoirs and the atmosphere, leading to changes in the atmosphere's ¹⁴C fraction. As the graph to the right shows, there is an overstatement of the age of the sample of nearly 1000 years in an uncalibrated dating of 7000 BP.

Aside from these changes due to natural processes, the level has also been affected by human activities. From the beginning of the industrial revolution in the 18th century to the 1950s, the fractional level of ¹⁴C decreased because of the admixture of large quantities of CO₂ into the atmosphere, due to the excavated oil reserves and combustion production of fossil fuel. This decline is known as the Suess effect, and also affects the ¹³C isotope. However, atmospheric ¹⁴C was almost doubled during the 1950s and 1960s due to atmospheric atomic bomb tests.^[16]

Calibration methods

The raw radiocarbon dates, in BP years, are calibrated to give calendar dates. Standard calibration curves are available, based on comparison of radiocarbon dates of samples that can be dated independently by other methods such as examination of tree growth rings (dendrochronology), deep ocean sediment cores, lake sediment varves, coral samples, and speleothems (cave deposits).

The calibration curves can vary significantly from a straight line, so comparison of uncalibrated radiocarbon dates (e.g., plotting them on a graph or subtracting dates to give elapsed time) is likely to give misleading results. There are also significant plateaus in the curves, such as the one from 11,000 to 10,000 radiocarbon years BP, which is believed to be associated with changing ocean circulation during the Younger Dryas period. Over the historical period from 0 to 10,000 years BP, the average width of the uncertainty of calibrated dates was found to be 335 years, although in well-behaved regions of the calibration curve the width decreased to about 113 years while in ill-behaved regions it increased to a maximum of 801 years. Significantly, in the ill-behaved regions of the calibration curve, increasing the precision of the measurements does not have a significant effect on increasing the accuracy of the dates.^[17]

The 2004 version of the calibration curve extends back quite accurately to 26,000 years BP. Any errors in the calibration curve do not contribute more than ±16 years to the measurement error during the historic and late prehistoric periods (0–6,000 yrs BP) and no more than ±163 years over the entire 26,000 years of the curve, although its shape can reduce the accuracy as mentioned above.^[18]

In late 2009, the journal Radiocarbon announced agreement on the INTCAL09 standard, which extends a more accurate calibration curve to 50,000 years.^[19][20]

History

Carbon dating was developed by American scientist Willard Libby and his team at the University of Chicago. Libby calculated the half-life of carbon-14 as 5568 ± 30 years, a figure now known as the Libby half-life. Following a conference at the University of Cambridge in 1962, a more accurate figure of 5730 ± 40 years was agreed upon based on more recent experimental data (this figure is now known as the Cambridge half-life).

The chairman of the Cambridge conference, Harry Godwin, wrote to the scientific journal Nature, recommending that the Libby half-life continue to be used for the time being, as the Cambridge figure might itself be improved by future experiments.^[21] Laboratories today continue to use the Libby figure to avoid inconsistencies with earlier publications, although the Cambridge half-life is still the most accurate figure that is widely known and accepted. However, the inaccuracy of the Libby half-life is not relevant if calibration is applied: the mathematical term representing the half-life is canceled out as long as the same value is used throughout a calculation.

Carbon exchange reservoir

Libby's original exchange reservoir hypothesis assumes that the exchange reservoir is constant all over the world. The calibration method also assumes that the temporal variation in ¹⁴C level is global, such that a small number of samples from a specific year are sufficient for calibration.^[22] However, since Libby's early work was published (1950 to 1958), latitudinal and continental variations in the carbon exchange reservoir have been observed by Hessel de Vries (1958;^[4] as reviewed by Lerman et al.^[23]). Subsequently, methods have been developed that allow the correction of these so-called reservoir effects, including:

• When CO₂ is transferred from the atmosphere to the oceans, it initially shares the ¹⁴C concentration of the atmosphere. However, turnaround times of CO₂ in the ocean are similar to the half-life of ¹⁴C (making ¹⁴C also a dating tool for ocean water).^[24] Marine organisms feed on this "old" carbon, and thus their radiocarbon age reflects the time of CO₂ uptake by the ocean rather than the time of death of the organism. This marine reservoir effect is partly handled by a special marine calibration curve,^[25] but local deviations of several hundred years exist.

• Erosion and immersion of carbonate rocks (which are generally older than 80,000 years and so shouldn't contain measurable ¹⁴C) causes an increase in ¹²C and ¹³C in the exchange reservoir, which depends on local weather conditions and can vary the ratio of carbon that living organisms incorporate. This is believed negligible for the atmosphere and atmosphere-derived carbon since most erosion will flow into the sea.^[26] The atmospheric ¹⁴C concentration may differ substantially from the concentration in local water reservoirs. Eroded from CaCO₃ or organic deposits, old carbon may be assimilated easily and provide diluted ¹⁴C carbon into trophic chains. So the method is less reliable for such materials as well as for samples derived from animals with such plants in their food chain.

• Volcanic eruptions eject large amount of carbon into the air, causing an increase in ¹²C and ¹³C in the exchange reservoir and can vary the exchange ratio locally. This explains the often irregular dating achieved in volcanic areas.^[26]

• The earth is not affected evenly by cosmic radiation, the magnitude of the radiation depends on land altitude and earth's magnetic field strength at any given location, causing minor variation in the local ¹⁴C production. This is accounted for by having calibration curves for different locations of the globe. However this could not always be performed, as tree rings for calibration were only recoverable from certain locations in 1958.^[27] The rebuttals by Münnich et al.^[4] and by Barker^[28] both maintain that while variations of carbon-14 exist, they are about an order of magnitude smaller than those implied by Crowe's calculations.

These effects were first confirmed when samples of wood from around the world, which all had the same age (based on tree ring analysis), showed deviations from the dendrochronological age. Calibration techniques based on tree-ring samples have contributed to increased accuracy since 1962, when they were accurate to 700 years at worst.^[29]

Speleothem studies extend ¹⁴C calibration

Speleothems (such as stalagmites) are calcium carbonate deposits that form from drips in limestone caves. Individual speleothems can be tens of thousands of years old.^[30] Scientists are attempting to extend the record of atmospheric carbon-14 by measuring radiocarbon in speleothems which have been independently dated using uranium-thorium dating.^[31][32] These results are improving the calibration for the radiocarbon technique and extending its usefulness to 45,000 years into the past.^[33] Initial results from a cave in the Bahamas suggested a peak in the amount of carbon-14 which was twice as high as modern levels.^[34] A recent study does not reproduce this extreme shift and suggests that analytical problems may have produced the anomalous result.^[32]

Examples

• Ancient footprints of Acahualinca
• Chauvet Cave
• Dolaucothi
• Eve of Naharon
• Haraldskær Woman
• Kennewick Man
• Shroud of Turin
• Skeleton Lake
• Thera eruption
• Vinland map

See also

• Carbon sequestration
• Cosmogenic isotopes
• Environmental isotopes
• Discussion of half-life and average-life or mean-lifetime
• Arizona Accelerator Mass Spectrometry Laboratory

References

1. ^ Plastino, W.; Kaihola, L.; Bartolomei, P.; Bella, F. (2001). "Cosmic Background Reduction In The Radiocarbon Measurement By Scintillation Spectrometry At The Underground Laboratory Of Gran Sasso". Radiocarbon 43 (2A): 157–161. https://digitalcommons.library.arizona.edu/objectviewer?o=http%3A%2F%2Fradiocarbon.library.arizona.edu%2Fvolume43%2Fnumber2A%2Fazu_radiocarbon_v43_n2a_157_161_v.pdf. 
2. ^ Arnold, J. R.; Libby, W. F. (1949). "Age Determinations by Radiocarbon Content: Checks with Samples of Known Age". Science 110 (2869): 678–680. Bibcode 1949Sci...110..678A. doi:10.1126/science.110.2869.678. PMID 15407879. http://hbar.phys.msu.ru/gorm/fomenko/libby.htm. 
3. ^ Willard Frank Libby
4. ^ ^{a b c} Münnich KO, Östlund HG, de Vries H (1958). "Carbon-14 Activity during the past 5,000 Years". Nature 182 (4647): 1432–3. Bibcode 1958Natur.182.1432M. doi:10.1038/1821432a0. 
5. ^ McFadgen, B G et al. (1994). "Radiocarbon calibration curve variations and their implications for the interpretation of New Zealand prehistory". Radiocarbon 36 (2): 221–236. http://digitalcommons.arizona.edu/objectviewer?o=http%3A%2F%2Fradiocarbon.library.arizona.edu%2FVolume36%2FNumber2%2Fazu_radiocarbon_v36_n2_221_236_v.pdf.  "The shape of a distribution of calibrated ¹⁴C dates displays spurious peaks and troughs, brought about by changes in the slope of the calibration curve interacting with the spreading effect of the stochastic distribution of counting errors"
6. ^ ^{a b} Ramsey, C. Bronk (2008). "Radiocarbon dating: revolutions in understanding". Archaeometry 50 (2): 249-275. doi:10.1111/j.1475-4754.2008.00394.x.  edit
7. ^ http://hypertextbook.com/facts/1997/MargaretKong.shtml
8. ^ Scott, EM (2003). "The Fourth International Radiocarbon Intercomparison (FIRI).". Radiocarbon 45: 135–285. 
9. ^ ^{a b} "NOSAMS Radiocarbon Data and Calculations". Woods Hole Oceanographic Institution. http://www.nosams.whoi.edu/clients/data.html. 
10. ^ Taylor RE, Southon J (2007). "Use of natural diamonds to monitor ¹⁴C AMS instrument backgrounds". Nuclear Instruments and Methods in Physics Research B 259: 282–28. Bibcode 2007NIMPB.259..282T. doi:10.1016/j.nimb.2007.01.239. 
11. ^ Stuiver M, Reimer PJ, Braziunas TF (1998). "High-precision radiocarbon age calibration for terrestrial and marine samples". Radiocarbon 40: 1127–51. http://depts.washington.edu/qil/datasets/uwten98_14c.txt. 
12. ^ "Atmospheric δ¹⁴C record from Wellington". Carbon Dioxide Information Analysis Center. http://cdiac.esd.ornl.gov/trends/co2/welling.html. Retrieved 1 May 2008. 
13. ^ "δ¹⁴CO₂ record from Vermunt". Carbon Dioxide Information Analysis Center. http://cdiac.esd.ornl.gov/trends/co2/cent-verm.html. Retrieved 1 May 2008. 
14. ^ "Radiocarbon dating". Utrecht University. http://www1.phys.uu.nl/ams/Radiocarbon.htm. Retrieved 1 May 2008. 
15. ^ Kudela K. and Bobik P. (2004). "Long-Term Variations of Geomagnetic Rigidity Cutoffs". Solar Physics 224: 423–431. Bibcode 2004SoPh..224..423K. doi:10.1007/s11207-005-6498-9. 
16. ^ Reimer, Paula J.; Brown, Thomas A.; Reimer, Ron W. (2004). "Discussion: Reporting and Calibration of Post-Bomb ¹⁴C Data". Radiocarbon 46 (3): 1299–1304 
17. ^ These results were obtained from a Monte Carlo analysis calibrating simulated measurements of varying precision using the 1993 version of the calibration curve. The width of the uncertainty represents a 2σ uncertainty (that is, a likelihood of 95% that the date appears between these limits). Niklaus TR, Bonani G, Suter M, Wölfli W (1994). "Systematic investigation of uncertainties in radiocarbon dating due to fluctuations in the calibration curve". Nuclear Instruments and Methods in Physics Research 92: 194–200. Bibcode 1994NIMPB..92..194N. doi:10.1016/0168-583X(94)96004-6. 
18. ^ Reimer Paula J et al. (2004). "INTCAL04 Terrestrial Radiocarbon Age Calibration, 0–26 Cal Kyr BP". Radiocarbon 46 (3): 1029–1058. http://digitalcommons.library.arizona.edu/objectviewer?o=http://radiocarbon.library.arizona.edu/Volume46/Number3/azu_radiocarbon_v46_n3_1029_1058_v.pdf.  A web interface is here.
19. ^ Reimer, P.J.; et. al. (2009). "IntCal09 and Marine09 Radiocarbon Age Calibration Curves, 0–50,000 Years cal BP". Radiocarbon 51 (4): 1111–1150. http://researchcommons.waikato.ac.nz/bitstream/10289/3622/1/Hogg%20Intcal09%20and%20Marine09.pdf. 
20. ^ Balter, Michael (15 Jan 2010). "Radiocarbon Daters Tune Up Their Time Machine". ScienceNOW Daily News. http://sciencenow.sciencemag.org/cgi/content/full/2010/115/3. 
21. ^ Godwin, H. (1962). "Half-life of Radiocarbon". Nature 195 (4845): 984. Bibcode 1962Natur.195..984G. doi:10.1038/195984a0. 
22. ^ Libby WF (1955). Radiocarbon dating (2nd ed.). Chicago: University of Chicago Press. 
23. ^ Lerman, J. C.; Mook, W. G.; Vogel, J. C.; de Waard, H. (1969). "Carbon-14 in Patagonian Tree Rings". Science 165 (3898): 1123–1125. Bibcode 1969Sci...165.1123L. doi:10.1126/science.165.3898.1123. PMID 17779805. 
24. ^ McNichol AP, Schneider RJ, von Reden KF, Gagnon AR, Elder KL, NOSAMS, Key RM, Quay PD (October 2000). "Ten years after - The WOCE AMS radiocarbon program". Nuclear Instruments and Methods in Physics Research, Section B: Beam Interactions with Materials and Atoms 172 (1–4): 479–84. Bibcode 2000NIMPB.172..479M. doi:10.1016/S0168-583X(00)00093-8. 
25. ^ Stuiver M, Braziunas TF (1993). "Modelling atmospheric ¹⁴C influences and ¹⁴C ages of marine samples to 10,000 BC". Radiocarbon 35 (1): 137. 
26. ^ ^{a b} Kolchin BA, Shez YA (1972). Absolute archaeological datings and their problems. Moscow: Nauka. 
27. ^ Crowe C (1958). "Carbon-14 activity during the past 5000 years". Nature 182 (4633): 470–1. Bibcode 1958Natur.182..470C. doi:10.1038/182470a0. 
28. ^ Barker H (1958). "Carbon-14 Activity during the past 5,000 Years". Nature 182 (4647): 1433. Bibcode 1958Natur.182.1433B. doi:10.1038/1821433a0. 
29. ^ Libby WF (1962). "Radiocarbon; an atomic clock". Annual Science and Humanity Journal. 
30. ^ Wang YJ; Cheng, H; Edwards, RL; An, ZS; Wu, JY; Shen, CC; Dorale, JA (2001). "A High-Resolution Absolute-Dated Late Pleistocene Monsoon Record from Hulu Cave, China". Science 294 (5550): 2345–2348. Bibcode 2001Sci...294.2345W. doi:10.1126/science.1064618. PMID 11743199. 
31. ^ Beck JW; Richards, DA; Edwards, RL; Silverman, BW; Smart, PL; Donahue, DJ; Hererra-Osterheld, S; Burr, GS et al. (2001). "Extremely large variations of atmospheric C-14 concentration during the last glacial period". Science 292 (5526): 2453–2458. Bibcode 2001Sci...292.2453B. doi:10.1126/science.1056649. PMID 11349137. 
32. ^ ^{a b} Hoffmann DL; Beck, J. Warren; Richards, David A.; Smart, Peter L.; Singarayer, Joy S.; Ketchmark, Tricia; Hawkesworth, Chris J. (2010). "Towards radiocarbon calibration beyond 28 ka using speleothems from the Bahamas". Earth and Planetary Science Letters 289: 1–10. Bibcode 2010E&PSL.289....1H. doi:10.1016/j.epsl.2009.10.004. 
33. ^ Jensen MN (2001). "Peering deep into the past". University of Arizona, Department of Physics. http://www.physics.arizona.edu/physics/public/beck-citizen.html. 
34. ^ Pennicott K (10 May 2001). "Carbon clock could show the wrong time". PhysicsWeb. http://physicsworld.com/cws/article/news/2676. 

Further reading

• Bowman, Sheridan (1990). Interpreting the Past: Radiocarbon Dating. Berkeley: University of California Press. ISBN 0520070372. 
• Currie, L. (2004). "The Remarkable Metrological History of Radiocarbon Dating II". J. Res. Natl. Inst. Stand. Technol. 109: 185–217. http://nvl.nist.gov/pub/nistpubs/jres/109/2/j92cur.pdf. 
• Friedrich, M.; et al. (2004). "The 12,460-Year Hohenheim Oak and Pine Tree-Ring Chronology from Central Europe—a Unique Annual Record for Radiocarbon Calibration and Paleoenvironment Reconstructions". Radiocarbon 46: 1111–1122. 
• Gove, H. E. (1999) From Hiroshima to the Iceman. The Development and Applications of Accelerator Mass Spectrometry. Bristol: Institute of Physics Publishing.
• Kovar, Anton J. (1966). "Problems in Radiocarbon Dating at Teotihuacan". American Antiquity (Society for American Archaeology) 31 (3): 427–430. doi:10.2307/2694748. JSTOR 2694748. 
• Lorenz, R. D.; Jull, A. J. T.; Lunine, J. I.; Swindle, T. (2002). "Radiocarbon on Titan". Meteoritics and Planetary Science 37 (6): 867–874. Bibcode 2002M&PS...37..867L. doi:10.1111/j.1945-5100.2002.tb00861.x. 
• Mook, W. G.; van der Plicht, J. (1999). "Reporting ¹⁴C activities and concentrations". Radiocarbon 41: 227–239. http://digitalcommons.library.arizona.edu/index.php/objectviewer?o=http://radiocarbon.library.arizona.edu/Volume41/Number3/azu_radiocarbon_v41_n3_227_239_v.pdf. 
• Weart, S. (2004) The Discovery of Global Warming - Uses of Radiocarbon Dating.
• Willis, E.H. (1996) Radiocarbon dating in Cambridge: some personal recollections. A Worm's Eye View of the Early Days.

External links

• Radiocarbon - The main international journal of record for research articles and date lists relevant to 14C
• C14dating.com - General information on Radiocarbon dating
• calib.org - Calibration program, Marine Reservoir database, and bomb calibration
• NOSAMS: National Ocean Sciences Accelerator Mass Spectrometry Facility at the Woods Hole Oceanographic Institution
• Discussion of calibration (from U Oxford)
• Several calibration programs can be found at www.radiocarbon.org
• CalPal Online (Cologne Radiocarbon Calibration & Paleoclimate Research Package)
• OxCal program (Oxford Calibration)
• Fairbanks' Radiocarbon Calibration program (for prior to 12400 BP)
• Notes on radiocarbon dating, including movies illustrating the atomic physics (from UC Santa Barbara)
• Carbon Dating-How it works?