Axonometric projection

For axonometric projection in video games, see Video games with isometric graphics.

Part of a series on:
Graphical projection
Planar Parallel projection Orthographic projection Multiviews Plan, or floor plan Section Elevation Auxiliary Axonometric projection (i.e. pictorials) Isometric projection Dimetric projection Trimetric projection Oblique projection Cavalier projection Cabinet projection Perspective projection Linear perspective One-point perspective Two-point perspective Three-point perspective Zero-point perspective Curvilinear perspective Reverse perspective
Other 3D projection Stereographic projection Anamorphic projection
Views Bird's-eye view/Aerial view Detail view 3/4 perspective Cutaway drawing Exploded view drawing Fisheye Fixed 3D Panorama Top-down perspective Worm's-eye view Zoom
Topics Computer graphics Computer-aided design Descriptive geometry Engineering drawing Foreshortening Map projection Projective geometry Technical drawing Vanishing point Video game graphics
v · d · e

Axonometric projection is a type of parallel projection, more specifically a type of orthographic projection, used to create a pictorial drawing of an object, where the object is rotated along one or more of its axes relative to the plane of projection.^[1]

There are three main types of axonometric projection: isometric, dimetric, and trimetric projection.

"Axonometric" means "to measure along axes". Axonometric projection shows an image of an object as viewed from a skew direction in order to reveal more than one side in the same picture.Whereas the term orthographic is sometimes reserved specifically for depictions of objects where the axis or plane of the object is parallel with the projection plane,^[2] in axonometric projection the plane or axis of the object is always drawn not parallel to the projection plane.

With axonometric projections the scale of distant features is the same as for near features, such pictures will look distorted, as it is not how our eyes or photography work. This distortion is especially evident if the object to view is mostly composed of rectangular features. Despite this limitation, axonometric projection can be useful for purposes of illustration.

History

The concept of an isometric had existed in a rough empirical form for centuries, well before Professor William Farish (1759–1837) of Cambridge University was the first to provide detailed rules for isometric drawing.^[3][4]

Farish published his ideas in the 1822 paper "On Isometrical Perspective", in which he recognized the "need for accurate technical working drawings free of optical distortion. This would lead him to formulate isometry. Isometry means "equal measures" because the same scale is used for height, width, and depth".^[5]

From the middle of the 19th century, according to Jan Krikke (2006)^[5] isometry became an "invaluable tool for engineers, and soon thereafter axonometry and isometry were incorporated in the curriculum of architectural training courses in Europe and the U.S. The popular acceptance of axonometry came in the 1920s, when modernist architects from the Bauhaus and De Stijl embraced it".^[5] De Stijl architects like Theo van Doesburg used axonometry for their architectural designs, which caused a sensation when exhibited in Paris in 1923".^[5]

Since the 1920s axonometry, or parallel perspective, has provided an important graphic technique for artists, architects, and engineers. Like linear perspective, axonometry helps depict 3D space on the 2D picture plane. It usually comes as a standard feature of CAD systems and other visual computing tools.^[6]

According to Jan Krikke (2000)^[6] however, "axonometry originated in China. Its function in Chinese art was similar to linear perspective in European art.^{[clarification needed]} Axonometry, and the pictorial grammar that goes with it, has taken on a new significance with the advent of visual computing".^[6]

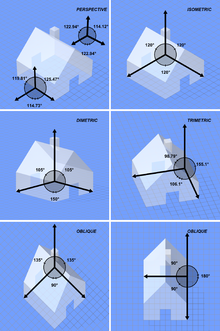Comparison of several types of graphical projection

• 

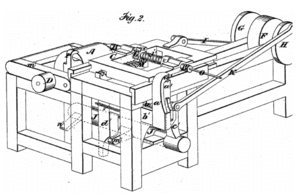
  Optical-grinding engine model (1822), drawn in 30° isometric perspective^[7]

• 

  Detail of the original version of Along the River During the Qingming Festival attributed to Zhang Zeduan (1085–1145)

• 

  Example of a dimetric axonometric drawing from a US Patent (1874)

• 

  Trimetric projection of the design of the Time Pyramid in Wemding, Germany

Three types of axonometric projections

The three types of axonometric projections are isometric projection, dimetric projection, and trimetric projection, depending on the exact angle at which the view deviates from the orthogonal.^[2][8] Typically in axonometric drawing, one axis of space is shown as the vertical.

• In isometric projection, the most commonly-used form of axonometric projection in engineering drawing,^[9] the direction of viewing is such that the three axes of space appear equally foreshortened, of which the displayed angles among them and also the scale of foreshortening are universally known. However in creating a final, isometric instrument drawing, in most cases a full-size scale, i.e., without using a foreshortening factor, is employed to good effect because the resultant distortion is difficult to perceive.^{[clarification needed]} Another advantage is that, in engineering drawings, 60° angles are more easily constructed using only a compass and straightedge.^{[clarification needed]}

• In dimetric projection, the direction of viewing is such that two of the three axes of space appear equally foreshortened, of which the attendant scale and angles of presentation are determined according to the angle of viewing; the scale of the third direction (vertical) is determined separately.

• In trimetric projection, the direction of viewing is such that all of the three axes of space appear unequally foreshortened. The scale along each of the three axes and the angles among them are determined separately as dictated by the angle of viewing. Trimetric perspective is seldom used,^[8] and is found in only a few video games (Fallout,^[10] SimCity 4^[11]).

Approximations are common in dimetric and trimetric drawings.^{[clarification needed]}

Limitations of axonometric projection

Drawing illustrating the limitations of axonometric projection

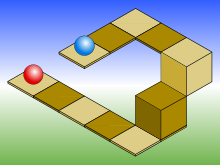
See also: Impossible object

As with all types of parallel projection, objects drawn with axonometric projection do not appear larger or smaller as they extend closer to or away from the viewer. While advantageous for architectural drawings, where measurements must be taken directly from the image, the result is a perceived distortion, since unlike perspective projection, this is not how our eyes or photography normally work. It also can easily result in situations where depth and altitude are difficult to gauge, as is shown in the illustration to the right.

In this isometric drawing, the blue sphere is two units higher than the red one. However, this difference in elevation is not apparent if one covers the right half of the picture, as the boxes (which serve as clues suggesting height) are then obscured.

This visual ambiguity has been exploited in op art, including "impossible object" drawings. M. C. Escher's Waterfall (1961) is a well-known example, in which a channel of water seems to travel unaided along a downward path, only to then paradoxically fall once again as it returns to its source. The water thus appears to disobey the law of conservation of energy.

References

1. ^ Gary R. Bertoline et al. (2002) Technical Graphics Communication‎. McGraw-Hill Professional, 2002. ISBN 0073655988, p.330.
2. ^ ^{a b} Maynard, Patric (2005). Drawing distinctions: the varieties of graphic expression. Cornell University Press. pp. 22. ISBN 0801472806. http://books.google.com/?id=4Y_YqOlXoxMC&pg=PA22&lpg=PA22&dq=axonometric+orthographic&q=axonometric%20orthographic. 
3. ^ Barclay G. Jones (1986). Protecting historic architecture and museum collections from natural disasters. University of Michigan. ISBN 0409900354. p.243.
4. ^ Charles Edmund Moorhouse (1974). Visual messages: graphic communication for senior students‎.
5. ^ ^{a b c d} J. Krikke (1996). "A Chinese perspective for cyberspace?". In: International Institute for Asian Studies Newsletter, 9, Summer 1996.
6. ^ ^{a b c} Jan Krikke (2000). "Axonometry: a matter of perspective". In: Computer Graphics and Applications, IEEE Jul/Aug 2000. Vol 20 (4), pp. 7-11.
7. ^ William Farish (1822) "On Isometrical Perspective". In: Cambridge Philosophical Transactions. 1 (1822).
8. ^ ^{a b} McReynolds, Tom; David Blythe (2005). Advanced graphics programming using openGL. Elsevier. pp. 502. ISBN 1558606599. http://books.google.com/?id=H4eYq7-2YhYC&pg=PA502&dq=axonometric+orthographic#v=onepage&q=axonometric%20orthographic. 
9. ^ Godse, A. P. (1980). Computer graphics. Technical Publications. pp. 29. ISBN 8184315589. http://books.google.com/?id=YkVp-2ZrmyMC&pg=PT224&dq=axonometric+orthographic#v=onepage&q=axonometric%20orthographic. 
10. ^ Green, Jeff (2000-02-29). "GameSpot Preview: Arcanum". GameSpot. CNET Networks, Inc. http://www.gamespot.com/features/arcanum_pre/. Retrieved 2008-01-10. 
11. ^ Butts, Steve (2003-09-09). "SimCity 4: Rush Hour Preview". IGN PC. IGN Entertainment, Inc. http://pc.ign.com/articles/437/437280p1.html. Retrieved 2008-01-10. 

Further reading

• Yve-Alain Bois, "Metamorphosis of Axonometry," Daidalos, no. 1 (1981), pp. 41–58