- Magnetohydrodynamics
-
Magnetohydrodynamics (MHD) (magneto fluid dynamics or hydromagnetics) is an academic discipline which studies the dynamics of electrically conducting fluids. Examples of such fluids include plasmas, liquid metals, and salt water or electrolytes. The word magnetohydrodynamics (MHD) is derived from magneto- meaning magnetic field, and hydro- meaning liquid, and -dynamics meaning movement. The field of MHD was initiated by Hannes Alfvén,[1] for which he received the Nobel Prize in Physics in 1970.
The fundamental concept behind MHD is that magnetic fields can induce currents in a moving conductive fluid, which in turn creates forces on the fluid and also changes the magnetic field itself. The set of equations which describe MHD are a combination of the Navier-Stokes equations of fluid dynamics and Maxwell's equations of electromagnetism. These differential equations have to be solved simultaneously, either analytically or numerically.
Contents
History
The first recorded use of the word magnetohydrodynamics is by Hannes Alfvén in 1942:
- "At last some remarks are made about the transfer of momentum from the Sun to the planets, which is fundamental to the theory (§11). The importance of the magnetohydrodynamic waves in this respect are pointed out."[2]
The ebbing salty water flowing past London's Waterloo Bridge interacts with the Earth's magnetic field to produce a potential difference between the two river-banks. Michael Faraday tried this experiment in 1832 but the current was too small to measure with the equipment at the time,[3] and the river bed contributed to short-circuit the signal. However, by the same process, Dr. William Hyde Wollaston was able to measure the voltage induced by the tide in the English Channel in 1851.[4]
Ideal and resistive MHD
 MHD Simulation of the Solar Wind
MHD Simulation of the Solar WindThe simplest form of MHD, Ideal MHD, assumes that the fluid has so little resistivity that it can be treated as a perfect conductor. This is the limit of infinite magnetic Reynolds number. In ideal MHD, Lenz's law dictates that the fluid is in a sense tied to the magnetic field lines. To explain, in ideal MHD a small rope-like volume of fluid surrounding a field line will continue to lie along a magnetic field line, even as it is twisted and distorted by fluid flows in the system. The connection between magnetic field lines and fluid in ideal MHD fixes the topology of the magnetic field in the fluid—for example, if a set of magnetic field lines are tied into a knot, then they will remain so as long as the fluid/plasma has negligible resistivity. This difficulty in reconnecting magnetic field lines makes it possible to store energy by moving the fluid or the source of the magnetic field. The energy can then become available if the conditions for ideal MHD break down, allowing magnetic reconnection that releases the stored energy from the magnetic field.
Ideal MHD equations
The ideal MHD equations consist of the continuity equation, the momentum equation, Ampere's Law neglecting displacement current, and a temperature evolution equation. As with any fluid description to a kinetic system, a closure approximation must be applied to highest moment of the particle distribution equation. This is often accomplished with approximations to the heat flux through a condition of adiabaticity or isothermality.
In the following,
 is the magnetic field,
is the magnetic field,  is the electric field,
is the electric field,  is the bulk plasma velocity,
is the bulk plasma velocity,  is the current density, ρ is the mass density, p is the plasma pressure, and t is time. The continuity equation is
is the current density, ρ is the mass density, p is the plasma pressure, and t is time. The continuity equation isThe momentum equation is
The Lorentz force term
 can be expanded to give
can be expanded to givewhere the first term on the right hand side is the magnetic tension force and the second term is the magnetic pressure force. The ideal Ohm's law for a plasma is given by
Faraday's law is
The low-frequency Ampere's law neglects displacement current and is given by
The magnetic divergence constraint is
The energy equation is given by
where γ = 5 / 3 is the ratio of specific heats for an adiabatic equation of state.
Applicability of ideal MHD to plasmas
Ideal MHD is only strictly applicable when:
- The plasma is strongly collisional, so that the time scale of collisions is shorter than the other characteristic times in the system, and the particle distributions are therefore close to Maxwellian.
- The resistivity due to these collisions is small. In particular, the typical magnetic diffusion times over any scale length present in the system must be longer than any time scale of interest.
- We are interested in length scales much longer than the ion skin depth and Larmor radius perpendicular to the field, long enough along the field to ignore Landau damping, and time scales much longer than the ion gyration time (system is smooth and slowly evolving).
Importance of resistivity
In an imperfectly conducting fluid the magnetic field can generally move through the fluid following a diffusion law with the resistivity of the plasma serving as a diffusion constant. This means that solutions to the ideal MHD equations are only applicable for a limited time for a region of a given size before diffusion becomes too important to ignore. One can estimate the diffusion time across a solar active region (from collisional resistivity) to be hundreds to thousands of years, much longer than the actual lifetime of a sunspot—so it would seem reasonable to ignore the resistivity. By contrast, a meter-sized volume of seawater has a magnetic diffusion time measured in milliseconds.
Even in physical systems which are large and conductive enough that simple estimates of the Lundquist number suggest that we can ignore the resistivity, resistivity may still be important: many instabilities exist that can increase the effective resistivity of the plasma by factors of more than a billion. The enhanced resistivity is usually the result of the formation of small scale structure like current sheets or fine scale magnetic turbulence, introducing small spatial scales into the system over which ideal MHD is broken and magnetic diffusion can occur quickly. When this happens, magnetic reconnection may occur in the plasma to release stored magnetic energy as waves, bulk mechanical acceleration of material, particle acceleration, and heat.
Magnetic reconnection in highly conductive systems is important because it concentrates energy in time and space, so that gentle forces applied to a plasma for long periods of time can cause violent explosions and bursts of radiation.
When the fluid cannot be considered as completely conductive, but the other conditions for ideal MHD are satisfied, it is possible to use an extended model called resistive MHD. This includes an extra term in Ampere's Law which models the collisional resistivity. Generally MHD computer simulations are at least somewhat resistive because their computational grid introduces a numerical resistivity.
Importance of kinetic effects
Another limitation of MHD (and fluid theories in general) is that they depend on the assumption that the plasma is strongly collisional (this is the first criterion listed above), so that the time scale of collisions is shorter than the other characteristic times in the system, and the particle distributions are Maxwellian. This is usually not the case in fusion, space and astrophysical plasmas. When this is not the case, or we are interested in smaller spatial scales, it may be necessary to use a kinetic model which properly accounts for the non-Maxwellian shape of the distribution function. However, because MHD is relatively simple and captures many of the important properties of plasma dynamics it is often qualitatively accurate and is almost invariably the first model tried.
Effects which are essentially kinetic and not captured by fluid models include double layers, Landau damping, a wide range of instabilities, chemical separation in space plasmas and electron runaway.
Structures in MHD systems
In many MHD systems most of the electric current is compressed into thin nearly-two-dimensional ribbons termed current sheets. These can divide the fluid into magnetic domains, inside of which the currents are relatively weak. Current sheets in the solar corona are thought to be between a few meters and a few kilometers in thickness, which is quite thin compared to the magnetic domains (which are thousands to hundreds of thousands of kilometers across). Another example is in the Earth's magnetosphere, where current sheets separate topologically distinct domains, isolating most of the Earth's ionosphere from the solar wind.
MHD waves
The wave modes derived using MHD plasma theory are called magnetohydrodynamic waves or MHD waves. In general there are three MHD wave modes:
- Pure (or oblique) Alfvén wave
- Slow MHD wave
- Fast MHD wave
All these waves have constant phase velocities for all frequencies, and hence there is no dispersion. At the limits when the angle between the wave propagation vector k and magnetic field B is either 0 (180) or 90 degrees, the wave modes are called[5]:
name type propagation phase velocity association medium other names Sound wave longitudinal 
adiabatic sound velocity none compressible, nonconducting fluid Alfvén wave transverse 
Alfvén velocity B shear Alfvén wave, the slow Alfvén wave, torsional Alfvén wave Magnetosonic wave longitudinal 
B, E compressional Alfvén wave, fast Alfvén wave, magnetoacoustic wave The MHD oscillations will be damped if the fluid is not perfectly conducting but has a finite conductivity, or if viscous effects are present.
MHD waves and oscillations are a popular tool for the remote diagnostics of laboratory and astrophysical plasmas, e.g. the corona of the Sun (Coronal seismology).
Extensions to magnetohydrodynamics
Resistive MHD
Resistive MHD describes magnetized fluids with finite electron diffusivity (
 ). This diffusivity leads to a breaking in the magnetic topology; magnetic field lines can 'reconnect' when they collide. Usually this term is small and reconnections can be handled by thinking of them as not dissimilar to shocks; this process has been shown to be important in the Earth-Solar magnetic interactions.
). This diffusivity leads to a breaking in the magnetic topology; magnetic field lines can 'reconnect' when they collide. Usually this term is small and reconnections can be handled by thinking of them as not dissimilar to shocks; this process has been shown to be important in the Earth-Solar magnetic interactions.Extended MHD
Extended MHD describes a class of phenomena in plasmas that are higher order than resistive MHD, but which can adequately be treated with a single fluid description. These include the effects of Hall physics, electron pressure gradients, finite Larmor Radii in the particle gyromotion, and electron inertia.
Two-Fluid MHD
Two-Fluid MHD describes plasmas that include a non-negligible Hall electric field. As a result, the electron and ion momenta must be treated separately. This description is more closely tied to Maxwell's equations as an evolution equation for the electric field exists.
Hall MHD
In 1960, M. J. Lighthill criticized the applicability of ideal or resistive MHD theory for plasmas.[6] It concerned the neglect of the "Hall current term", a frequent simplification made in magnetic fusion theory. Hall-magnetohydrodynamics (HMHD) takes into account this electric field description of magnetohydrodynamics. The most important difference is that in the absence of field line breaking, the magnetic field is tied to the electrons and not to the bulk fluid.[7]
Collisionless MHD
MHD is also often used for collisionless plasmas. In that case the MHD equations are derived from the Vlasov equation.[8]
Applications
Geophysics
Earth's Core
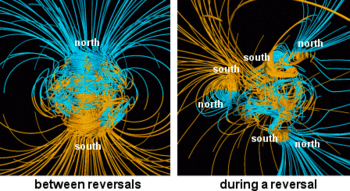
Beneath the Earth's mantle, lies the core which is made up of two parts - the solid inner core and liquid outer core - both have significant quantities of iron. The liquid outer core moves in the presence of the magnetic field and eddies are set up into the same due to the Coriolis effect. These eddies develop a magnetic field which boosts Earth's original magnetic field - a process which is self-sustaining and is called as the geomagnetic dynamo. [9]
Based on the MHD equations, Glatzmaier and Paul Roberts have made a supercomputer model of the Earth's interior. After running the simulations for thousands of years in virtual time, the changes in Earth's magnetic field can be studied. The simulation results are in good agreement with the observations as the simulations have correctly predicted that the Earth's magnetic field flips every few thousands of years. During the flips, the magnetic field doesn't vanish altogether - it just gets more complicated. [10]
Astrophysics
MHD applies quite well to astrophysics since over 99% of baryonic matter content of the Universe is made up of plasma, including stars, the interplanetary medium (space between the planets), the interstellar medium (space between the stars), nebulae and jets. Many astrophysical systems are not in local thermal equilibrium, and therefore require an additional kinematic treatment to describe all the phenomena within the system (see Astrophysical plasma).
Sunspots are caused by the Sun's magnetic fields, as Joseph Larmor theorized in 1919. The solar wind is also governed by MHD. The differential solar rotation may be the long term effect of magnetic drag at the poles of the Sun, an MHD phenomenon due to the Parker spiral shape assumed by the extended magnetic field of the Sun.
Previously, theories describing the formation of the Sun and planets could not explain how the Sun has 99.87% of the mass, yet only 0.54% of the angular momentum in the solar system. In a closed system such as the cloud of gas and dust from which the Sun was formed, mass and angular momentum are both conserved. That conservation would imply that as the mass concentrated in the center of the cloud to form the Sun, it would spin up, much like a skater pulling their arms in. The high speed of rotation predicted by early theories would have flung the proto-Sun apart before it could have formed. However, magnetohydrodynamic effects transfer the Sun's angular momentum into the outer solar system, slowing its rotation.
Breakdown of ideal MHD (in the form of magnetic reconnection) is known to be the cause of solar flares, the largest explosions in the solar system. The magnetic field in a solar active region over a sunspot can become quite stressed over time, storing energy that is released suddenly as a burst of motion, X-rays, and radiation when the main current sheet collapses, reconnecting the field.
Engineering
MHD is related to engineering problems such as plasma confinement, liquid-metal cooling of nuclear reactors, and electromagnetic casting (among others).
The first prototype of this kind of propulsion was built and tested in 1965 by Steward Way, a professor of mechanical engineering at the University of California, Santa Barbara. Way, on leave from his job at Westinghouse Electric, assigned his senior year undergraduate students to develop a submarine with this new propulsion system.[11] In early 1990s, Mitsubishi built a boat, the 'Yamato,' which uses a magnetohydrodynamic drive, is driven by a liquid helium-cooled superconductor, and can travel at 15 km/h. [12]
MHD power generation fueled by potassium-seeded coal combustion gas showed potential for more efficient energy conversion (the absence of solid moving parts allows operation at higher temperatures), but failed due to cost prohibitive technical difficulties.[13]
In microfluidic devices, the MHD pump is so far the most effective for producing a continuous, nonpulsating flow in a complex microchannel design. It was used to implement a PCR protocol.[citation needed]
Magnetic Drug Targeting
Latest research on cancer is partly focused on localized delivery of cancer medicine to the affected part of the body. To achieve the same the medicine is bound to magnetic particles (e.g. ferrofluids) which are biologically compatible. For targeting the same permanent magnets can be used by positioning them at suitable locations of the external body. To study the interaction between the magnetic fluid particles passing through the blood with the external magnetic field, magnetohydrodynamic equations and finite element analysis are used. Thus the efficacy of such treatments can be estimated. [14]
See also
- Electrohydrodynamics
- Plasma stability
- Shocks and discontinuities (magnetohydrodynamics)
- Computational magnetohydrodynamics
- Ferrofluid
- MHD generator
- MHD sensor
- Magnetic flow meter
- Magnetohydrodynamic turbulence
- Molten salt
- Electromagnetic pump
Notes
- ^ Alfvén, H., "Existence of electromagnetic-hydrodynamic waves" (1942) Nature, Vol. 150, pp. 405
- ^ Alfvén, H., "On the cosmogony of the solar system III", Stockholms Observatoriums Annaler, vol. 14, pp.9.1-9.29
- ^ Dynamos in Nature by David P. Stern
- ^ McKetta J McKetta, "Encyclopedia of Chemical Processing and Design: Volume 66" (1999)
- ^ MHD waves [Oulu]
- ^ M. J. Lighthill, "Studies on MHD waves and other anisotropic wave motion," Phil. Trans. Roy. Soc., London, vol. 252A, pp. 397-430, 1960.
- ^ E.A. Witalis, "Hall Magnetohydrodynamics and Its Applications to Laboratory and Cosmic Plasma", IEEE Transactions on Plasma Science (ISSN 0093-3813), vol. PS-14, Dec. 1986, p. 842-848.
- ^ W. Baumjohann and R. A. Treumann, Basic Space Plasma Physics, Imperial College Press, 1997
- ^ http://www.pbs.org/wgbh/nova/magnetic/reve-drives.html
- ^ http://science.nasa.gov/science-news/science-at-nasa/2003/29dec_magneticfield/
- ^ "Run Silent, Run Electromagnetic". Time. 1966-09-23. http://www.time.com/time/magazine/article/0,9171,842848-1,00.html.
- ^ Setsuo Takezawa et al. (March 1995) Operation of the Thruster for Superconducting Electromagnetohydrodynamic Propu1sion Ship YAMATO 1
- ^ Partially Ionized Gases, M. Mitchner and Charles H. Kruger, Jr., Mechanical Engineering Department, Stanford University. See Ch. 9 "Magnetohydrodynamic (MHD) Power Generation", p. 214-230.
- ^ http://www.comsol.com/multiphysics/magnetohydrodynamics/
References
- Bansal, J. L. (1994) Magnetofluiddynamics of Viscous Fluids Jaipur Publishing House, Jaipur, India, OCLC 70267818
- Barbu, V. et al. (2003) "Exact controllability magneto-hydrodynamic equations" Communications on Pure and Applied Mathematics 56: pp. 732–783.
- Biskamp, Dieter. Nonlinear Magnetohydrodynamics. Cambridge, England: Cambridge University Press, 1993. 378 p. ISBN 0-521-59918-0
- Calvert, James B. (20 October 2002) "Magnetohydrodynamics: The dynamics of conducting fluids in an electromagnetic field" (self published by an Associate Professor Emeritus of Engineering, University of Denver, U.S.A.)
- Davidson, Peter Alan (May 2001) An Introduction to Magnetohydrodynamics Cambridge University Press, Cambridge, England, ISBN 0-521-79487-0
- Faraday, M. (1832). "Experimental Researches in Electricity." First Series, Philosophical Transactions of the Royal Society, pp. 125–162.
- Ferraro, Vincenzo Consolato Antonio and Plumpton, Charles. An Introduction to Magneto-Fluid Mechanics, 2nd ed.
- Havarneanu, T.; Popa, C. and Sritharan, S. S. (2006) "Exact Internal Controllability for Magneto-Hydrodynamic Equations in Multi-connected Domains" Advances in Differential Equations 11(8): pp. 893–929.
- Hughes, William F. and Young, Frederick J. (1966) The Electromagnetodynamics of Fluids John Wiley, New York, OCLC 440919050
- Hurricane, O. A.; Fong, B. H. and Cowley, S. C. (October 1997) "Nonlinear magnetohydrodynamic detonation: Part I" Physics of Plasmas 4(10): pp. 3565–3580.
- Jordan, R. (July 1995) "A statistical equilibrium model of coherent structures in magnetohydrodynamics", Nonlinearity 8: pp. 585–613.
- Kerrebrock, J. L. (April 1965) "Magnetohydrodynamic Generators with Nonequilibrium Ionization", AIAA Journal, 3(4): pp. 591–601, doi: 10.2514/3.2934.
- Kulikovskiy, Andreĭ G. and Lyubimov, Grigoriĭ A. (1965)Magnetohydrodynamics. Addison-Wesley, Reading, Massachusetts, OCLC 498979430
- Lorrain, Paul ; Lorrain, François and Houle, Stéphane (2006) Magneto-fluid dynamics: fundamentals and case studies of natural phenomena Springer, New York, ISBN 0-387-33542-0
- Pai, Shih-I (1962) Magnetogasdynamics and Plasma Dynamics Springer-Verlag, Vienna, ISBN 0-387-80608-3
- Popa, C. and Sritharan, S. S. (2003) "Fluid-magnetic splitting methods for magneto-hydrodynamics" Mathematical Methods and Models in Applied Sciences 13(6): pp. 893–917.
- Roberts, Paul H. (1967) An Introduction to Magnetohydrodynamics Longmans Green, London, OCLC 489632043
- Rosa, Richard J. (1987) Magnetohydrodynamic Energy Conversion (2nd edition) Hemisphere Publishing, Washington, D.C., ISBN 0-89116-690-4
- Sritharan, S. S. and Sundar, P. (1999) "The stochastic magneto-hydrodynamic system" Infinite Dimensional Analysis, Quantum Probability and Related Topics (e-journal) 2(2): pp. 241–265.
- Stern, David P. "The Sun's Magnetic Cycle" In Stern, David P. The Great Magnet, the Earth United States National Aeronautics and Space Administration
- Sutton, George W., and Sherman, Arthur (1965) Engineering Magnetohydrodynamics, McGraw-Hill Book Company, New York, OCLC 537669
- Tabar, M. R. Rahimi, and Rouhani, S. (March 1995) "Turbulent Two Dimensional Magnetohydrodynamics and Conformal Field Theory" Department of Physics, Sharif University of Technology. Institute for Studies in Theoretical Physics and Mathematics. Volume 1. Tehran, Iran. arXiv:hep-th/9503005
- Van Wie, D. M. (2005) Future Technologies – Application of Plasma Devices for Vehicle Systems, The Johns Hopkins University, Applied Physics Laboratory – Laurel, Maryland, USA – NATO Document
- West, Jonathan et al. (2002) "Application of magnetohydrodynamic actuation to continuous flow chemistry" Lab on a Chip 2: pp. 224–230
- "Magnetohydrodynamics" In Zumerchik, John (editor) (2001) Macmillan Encyclopedia of Energy Macmillan Reference USA, New York, ISBN 0-02-865895-7
Fusion power Core topics Nuclear fusion processes and methods Gravitational confinement - Alpha process
- Triple-alpha process
- Proton-proton chain
- Helium flash
- CNO cycle
- Lithium burning
- Carbon burning
- Neon burning
- Oxygen burning
- Silicon burning
- S-process
- R-process
- Fusor
- Nova (Remnants)
Magnetic confinement Inertial confinement - Laser-driven
- Bubble fusion (acoustic)
- Fusor (electrostatic)
- Magnetized target
- H-bomb
- Pure fusion bomb
Spatial confinement Other forms Fusion experimental devices by confinement method Magnetic InternationalAmericasAsiaEurope JET •
JET •  Tore Supra · TFR •
Tore Supra · TFR •  ASDEX Upgrade · TEXTOR •
ASDEX Upgrade · TEXTOR •  FTU · IGNITOR •
FTU · IGNITOR •  T-15 •
T-15 •  TCV •
TCV •  MAST · START •
MAST · START •  COMPASS-DOther
COMPASS-DOtherInertial LaserAmericasAsiaEuropeNon-laserCategories:- Fluid dynamics
- Plasma physics
- Fundamental physics concepts
- Space plasmas
- Magnetohydrodynamics
Wikimedia Foundation. 2010.