Lawson criterion

In nuclear fusion research, the Lawson criterion, first derived on fusion reactors (initially classified) by John D. Lawson in 1955 and published in 1957,^[1] is an important general measure of a system that defines the conditions needed for a fusion reactor to reach ignition, that is, that the heating of the plasma by the products of the fusion reactions is sufficient to maintain the temperature of the plasma against all losses without external power input. As originally formulated the Lawson criterion gives a minimum required value for the product of the plasma (electron) density n_e and the "energy confinement time" τ_E. Later analyses suggested that a more useful figure of merit is the "triple product" of density, confinement time, and plasma temperature T. The triple product also has a minimum required value, and the name "Lawson criterion" often refers to this inequality.

The product n_eτ_E

The confinement time τ_E measures the rate at which a system loses energy to its environment. It is the energy content W divided by the power loss P_loss (rate of energy loss):

$\tau_E = \frac{W}{P_{\rm loss}}$

For a fusion reactor to operate in steady state, as magnetic fusion energy schemes usually entail, the fusion plasma must be maintained at a constant temperature. Thermal energy must therefore be added to it (either directly by the fusion products or by recirculating some of the electricity generated by the reactor) at the same rate the plasma loses energy (for instance by heat conduction to the device walls or radiation losses like bremsstrahlung).

For illustration, the Lawson criterion for the D-T reaction will be derived here, but the same principle can be applied to other fusion fuels. It will also be assumed that all species have the same temperature, that there are no ions present other than fuel ions (no impurities and no helium ash), and that D and T are present in the optimal 50-50 mixture.^[2] In that case, the ion density is equal to the electron density and the energy density of both together is given by

W = 3n_ek_BT

where k_B is the Boltzmann constant.

The volume rate f (reactions per volume per time) of fusion reactions is

$f = n_D n_T \langle\sigma v\rangle = \frac{1}{4}n_e^2 \langle\sigma v\rangle$

where σ is the fusion cross section, v is the relative velocity, and < > denotes an average over the Maxwellian velocity distribution at the temperature T.

The volume rate of heating by fusion is f times E_ch, the energy of the charged fusion products (the neutrons cannot help to keep the plasma hot). In the case of the D-T reaction, E_ch = 3.5 MeV.

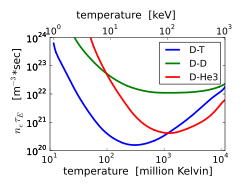The Lawson criterion, or minimum value of (electron density * energy confinement time) required for self-heating, for three fusion reactions. For DT, n_eτ_E minimizes near the temperature 25 keV (300 million kelvins).

The Lawson criterion is the requirement that the fusion heating exceed the losses:

$f E_{ch} \ge P_{loss}$

$\leftrightarrow$

$\frac{1}{4}n_e^2 \langle\sigma v\rangle E_{ch} \ge \frac{3n_ek_BT}{\tau_E}$

$\leftrightarrow$

$n_{\rm e} \tau_{\rm E} \ge L \equiv \frac{12}{E_{\rm ch}}\,\frac{k_{\rm B}T}{\langle\sigma v\rangle}$

The quantity $\frac{T}{\langle\sigma v\rangle}$ is a function of temperature with an absolute minimum. Replacing the function with its minimum value provides an absolute lower limit for the product n_eτ_e. This is the Lawson criterion.

For the D-T reaction, the physical value is at least

$n_{\rm e} \tau_{\rm E} \ge 1.5\times10^{20} {\rm s}/\mbox{m}^3$

The minimum of the product occurs near T = 25 keV.

The "triple product" n_eTτ_E

A still more useful figure of merit is the "triple product" of density, temperature, and confinement time, n_eTτ_E. For most confinement concepts, whether inertial, mirror, or toroidal confinement, the density and temperature can be varied over a fairly wide range, but the maximum pressure attainable is a constant. When that is the case, the fusion power density is proportional to $p^2\langle\sigma v\rangle/T^2$. Therefore the maximum fusion power available from a given machine is obtained at the temperature where $\langle\sigma v\rangle/T^2$ is a maximum. Following the derivation above, it is easy to show the inequality

$n_{\rm e} T \tau_{\rm E} \ge \frac{12k_{\rm B}}{E_{\rm ch}}\,\frac{T^2}{\langle\sigma v\rangle}$

The fusion triple product condition for three fusion reactions.

For the special case of tokamaks there is an additional motivation for using the triple product. Empirically, the energy confinement time is found to be nearly proportional to n^1/3/P^2/3. In an ignited plasma near the optimum temperature, the heating power P is equal to the fusion power and therefore proportional to n²T². The triple product scales as

nTτ $\propto$ nT (n^1/3/P^2/3) $\propto$ nT (n^1/3/(n²T²)^2/3) $\propto$ T ^-1/3

Thus the triple product is only a weak function of density and temperature and therefore a good measure of the efficiency of the confinement scheme.

The quantity $\frac{T^2}{\langle\sigma v\rangle}$ is also a function of temperature with an absolute minimum at a slightly lower temperature than $\frac{T}{\langle\sigma v\rangle}$.

For the D-T reaction, the physical value is about

$n_{\rm e} T \tau_E \ge 10^{21} \mbox{keV s}/\mbox{m}^3$

This number has not yet been achieved in any reactor, although the latest generations of machines have come close. For instance, the TFTR has achieved the densities and energy lifetimes needed to achieve Lawson at the temperatures it can create, but it cannot create those temperatures at the same time. ITER aims to do both.

Inertial confinement

The Lawson criterion applies to inertial confinement fusion as well as to magnetic confinement fusion but is more usefully expressed in a different form. Whereas the energy confinement time in a magnetic system is very difficult to predict or even to establish empirically, in an inertial system it must be on the order of the time it takes sound waves to travel across the plasma:

$\tau_E \approx R/\sqrt{k_BT/m_i}$

Following the above derivation of the limit on n_eτ_E, we see that the product of the density and the radius R must be greater than a value related to the minimum of T^3/2/<σv>. This condition is traditionally expressed in terms of the mass density ρ:

ρR > 1 g/cm²

To satisfy this criterion at the density of solid D-T (0.2 g/cm³) would require an implausibly large laser pulse energy. Assuming the energy required scales with the mass of the fusion plasma (E_laser ~ ρR³ ~ ρ^-2), compressing the fuel to 10³ or 10⁴ times solid density would reduce the energy required by a factor of 10⁶ or 10⁸, bringing it into a realistic range. With a compression by 10³, the compressed density will be 200 g/cm³, and the compressed radius can be as small as 0.05 mm. The radius of the fuel before compression would be 0.5 mm. The initial pellet will be perhaps twice as large since most of the mass will be ablated during the compression.

The fusion power density is a good figure of merit to determine the optimum temperature for magnetic confinement, but for inertial confinement the fractional burn-up of the fuel is probably more useful. The burn-up should be proportional to the specific reaction rate (n²<σv>) times the confinement time (which scales as T^-1/2) divided by the particle density n:

burn-up fraction ~ n²<σv> T^-1/2 / n ~ (nT) (<σv>/T^3/2)

Thus the optimum temperature for inertial confinement fusion is that which maximizes <σv>/T^3/2, which is slightly higher than the optimum temperature for magnetic confinement.

See also

• Fusion energy gain factor (Q)

Notes

1. ^ J. D. Lawson, "Some Criteria for a Power Producing Thermonuclear Reactor", Proceedings of the Physical Society B, Volume 70 (1957), p. 6
2. ^ It is straightforward to relax these assumptions. The most difficult question is how to define n when the ion and electrons differ in density and temperature. Considering that this is a calculation of energy production and loss by ions, and that any plasma confinement concept must contain the pressure forces of the plasma, it seems appropriate to define the effective (electron) density n through the (total) pressure p as n = p/2T_i. The factor of 2 is included because n usually refers to the density of the electrons alone, but p here refers to the total pressure. Given two species with ion densities n_1,2, atomic numbers Z_1,2, ion temperature T_i, and electron temperature T_e, it is easy to show that the fusion power is maximized by a fuel mix given by n₁/n₂ = (1+Z₂T_e/T_i)/(1+Z₁T_e/T_i). The values for nτ, nTτ, and the power density must be multiplied by the factor (1+Z₁T_e/T_i)×(1+Z₂T_e/T_i)/4. For example, with protons and boron (Z=5) as fuel, another factor of 3 must be included in the formulas. On the other hand, for cold electrons, the formulas must all be divided by 4 (with no additional factor for Z>1).

External links

The mathematical derivation is reproduced here.