Resonance (chemistry)

For other uses, see Resonance (disambiguation).

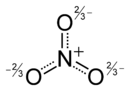
Two of the contributing structures of nitrogen dioxide

In chemistry, resonance or mesomerism ^[1] is a way of describing delocalized electrons within certain molecules or polyatomic ions where the bonding cannot be expressed by one single Lewis formula. A molecule or ion with such delocalized electrons is represented by several contributing structures ^[2] (also called resonance structures or canonical forms).

Each contributing structure can be represented by a Lewis structure, with only an integer number of covalent bonds between each pair of atoms within the structure.^[3] Several Lewis structures are used collectively to describe the actual molecular structure. However these individual contributors cannot be observed in the actual resonance-stabilized molecule; the molecule does not oscillate back and forth between the contributing structures, as might be assumed from the word "resonance". The actual structure is an approximate intermediate between the canonical forms, but its overall energy is lower than each of the contributors. This intermediate form between different contributing structures is called a resonance hybrid.^[4] Contributing structures differ only in the position of electrons, not in the position of nuclei.
Resonance is a key component of valence bond theory.

Electron delocalization lowers the potential energy of the substance and thus makes it more stable than any of the contributing structures. The difference between the potential energy of the actual structure and that of the contributing structure with the lowest potential energy is called the resonance energy^[5] or delocalization energy.

Resonance is distinguished from tautomerism and conformational isomerism, which involve the formation of isomers, thus the rearrangement of the nuclear positions.

General characteristics of resonance

Molecules and ions with resonance (also called mesomerism) have the following basic characteristics:

Contributing structures of the carbonate ion

• They can be represented by several correct Lewis formulas, called "contributing structures", "resonance structures" or "canonical forms". However, the real structure is not a rapid interconversion of contributing structures. Several Lewis structures are used together, because none of them exactly represents the actual structure. To represent the intermediate, a resonance hybrid is used instead.
• The contributing structures are not isomers. They differ only in the position of electrons, not in the position of nuclei.
• Each Lewis formula must have the same number of valence electrons (and thus the same total charge), and the same number of unpaired electrons, if any.^[6]
• Bonds that have different bond orders in different contributing structures do not have typical bond lengths. Measurements reveal intermediate bond lengths.
• The real structure has a lower total potential energy than each of the contributing structures would have. This means that it is more stable than each separate contributing structure would be.

Use of contributing structures

In Lewis formulas, covalent bonds are represented in accordance with the valence bond theory. Each single bond is made by two valence electrons, localized between the two bonded atoms. Each double bond has two additional localized π electrons, while each triple bond has four additional π electrons (two pairs) between the bonded atoms.

In molecules or ions that have a combination of one or more single and multiple bonds, often the exact position of the respective bonds in the Lewis formula cannot be indicated. The π electrons appear to be delocalized and the multiple bonds could be in different positions. In those cases the molecule cannot be represented by one single Lewis formula. To solve this problem, in valence bond theory the concept of resonance is used, and the molecule is represented by several contributing structures, each showing a possible distribution of single and multiple bonds. The molecular orbital theory already includes the concept of delocalized electrons and therefore has no need of the concept of resonance.

None of the contributing structures is considered to represent the actual structure, since bonds that have a different bond order in different contributing structures do not have, if measured, a bond length that is typical for a normal single or multiple bond. Moreover, the overall energy of the actual structure is lowered with the resonance energy.

Resonance hybrids

The actual structure of a molecule in the normal quantum state has the lowest possible value of total energy. This structure is called the "resonance hybrid" of that molecule. The resonance hybrid is the approximate intermediate of the contributing structures, but the overall energy is lower than each of the contributors, due to the resonance energy. ^[4]

Major and minor contributors

One contributing structure may resemble the actual molecule more than another (in the sense of energy and stability). Structures with a low value of potential energy are more stable than those with high values and resemble the actual structure more. The most stable contributing structures are called major contributors. Energetically unfavourable and therefore less probable structures are minor contributors.
Major contributors are generally structures

• that obey as much as possible the octet rule (8 valence electrons around each atom rather than having deficiencies or surplus)
• that have a maximum number of covalent bonds
• that carry a minimum of charged atoms
• with negative charge, if any, on the most electronegative atoms and positive charge, if any, on the most electropositive.

The greater the number of contributing structures, the more stable the molecule. This is because the more states at lower energy are available to the electrons in a particular molecule, the more stable the electrons are. Also the more volume electrons can occupy at lower energy the more stable the molecule is.

Equivalent contributors contribute equally to the actual structure; those with low potential energy (the major contributors) contribute more to the resonance hybrid than the less stable minor contributors. Especially when there is more than one major contributor, the resonance stabilization is high. High values of resonance energy are found in aromatic molecules.

Contributing structures in diagrams

Contributing structures of the thiocyanate ion, enclosed in square brackets.

Hybrid of the nitrate ion		Hybrid of benzene.

In diagrams, contributing structures are typically separated by double-headed arrows (). The arrow should not be confused with the right and left pointing equilibrium arrow (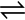). All structures together may be enclosed in large square brackets, to indicate they picture one single molecule or ion, not different species in a chemical equilibrium.

Alternatively to the use of resonance structures in diagrams, a hybrid diagram can be used. In a hybrid diagram, pi bonds that are involved in resonance are usually pictured as curves ^[7] or dashed lines, indicating that these are partial rather than normal complete pi bonds. In benzene and other aromatic rings, the delocalized pi-electrons are sometimes pictured as a solid circle.^[8]

Bond lengths

Resonance structures of benzene

Comparing the two contributing structures of benzene, all single and double bonds are interchanged. Bond lengths can be measured, for example using X-ray diffraction. The average length of a C-C single bond is 154 pm; that of a C=C double bond is 133 pm. In localized cyclohexatriene, the carbon-carbon bonds should be alternating 154 and 133 pm. Instead, all carbon-carbon bonds in benzene are found to be about 139 pm, a bond length intermediate between single and double bond. This mixed single and double bond (or triple bond) character is typical for all molecules in which bonds have a different bond order in different contributing structures.

Resonance energy

Every structure is associated with a certain quantity of energy, which determines the stability of the molecule or ion (the lower energy, the greater stability). A resonance hybrid has a structure that is intermediate between the contributing structures; the total quantity of potential energy, however, is lower than the intermediate. Hybrids are therefore always more stable than any of the contributing structures would be.^[9] The molecule is sometimes said to be "stabilized by resonance" or "resonance-stabilized," but the stabilization derives from electron delocalization, of which "resonance" is only a description. Delocalization of the π-electrons lowers the orbital energies, imparting this stability. The difference between the potential energy of the actual structure (the resonance hybrid) and that of the contributing structure with the lowest potential energy is called the "resonance energy".^[5]

Resonance energy of benzene

Resonance (or delocalization) energy is the amount of energy needed to convert the true delocalized structure into that of the most stable contributing structure. The empirical resonance energy can be estimated by comparing the enthalpy change of hydrogenation of the real substance with that estimated for the contributing structure.

The complete hydrogenation of benzene to cyclohexane via 1,3-cyclohexadiene and cyclohexene is exothermic; 1 mole benzene delivers 208.4 kJ (49.8 kcal).

Hydrogenation of one double bond delivers 119.7 kJ (28.6 kcal), as can be deduced from the last step, the hydrogenation of cyclohexene. In benzene, however, 23.4 kJ (5.6 kcal) are needed to hydrogenate one double bond. The difference, being 143.1 kJ (34.2 kcal), is the empirical resonance energy of benzene. Because 1,3-cyclohexadiene also has a small delocalization energy (7.6 kJ or 1.8 kcal/mol) the net resonance energy, relative to the localized cyclohexatriene, is a bit higher: 151 kJ or 36 kcal/mol. ^[10]

This measured resonance energy is also the difference between the hydrogenation energy of three 'non-resonance' double bonds and the measured hydrogenation energy:

(3 × 119.7) − 208.4 = 150.7 kJ/mol (36 kcal).^[11]

Note: The values used here are from the article of Wiberg, Nakaji, Morgan (1993). Values from other sources may differ.

Resonance in quantum mechanics

Resonance has a deeper significance in the mathematical formalism of valence bond theory (VB). When a molecule cannot be represented by the standard tools of valence bond theory (promotion, hybridisation, orbital overlap, sigma and π bond formation) because no single structure predicted by VB can account for all the properties of the molecule, one invokes the concept of resonance.

Valence bond theory gives us a model for benzene where each carbon atom makes two sigma bonds with its neighbouring carbon atoms and one with a hydrogen atom. But since carbon is tetravalent, it has the ability to form one more bond. In VB it can form this extra bond with either of the neighbouring carbon atoms, giving rise to the familiar Kekulé ring structure. But this cannot account for all carbon-carbon bond lengths being equal in benzene. A solution is to write the actual wavefunction of the molecule as a linear superposition of the two possible Kekulé structures (or rather the wavefunctions representing these structures), creating a wavefunction that is neither of its components but rather a superposition of them.

In benzene both Kekulé structures have equal energy and are equal contributors to the overall structure—the superposition is an equally-weighted average, or a 1:1 linear combination of the two—but this need not be the case. In general, the superposition is written with undetermined coefficients, which are then variationally optimized to find the lowest possible energy for the given set of basis wavefunctions. This is taken to be the best approximation that can be made to the real structure, though a better one may be made with addition of more structures.

Molecular orbital (MO) versus valence bond (VB) theory

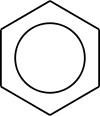
In molecular orbital theory, the main alternative to valence bond theory, resonance often (but not always) translates to a delocalization of electrons in π orbitals (which are a separate concept from π bonds in VB). In MO theory, the molecular orbitals (MOs) are approximated as sums of all the atomic orbitals AOs on all the atoms; there are as many MOs as AOs. Each AO_i has a weighting coefficient c_i that indicates the AO's contribution to a particular MO. For example, in benzene, the MO model gives us 6 π MOs which are combinations of the 2p_z AOs on each of the 6 C atoms. Thus, each π MO is delocalized over the whole benzene molecule and any electron occupying an MO will be delocalized over the whole molecule. This MO interpretation has inspired the picture of the benzene ring as a hexagon with a circle inside. When describing benzene, the VB concept of localized sigma 'bonds' and the MO concept of 'delocalized' π electrons are frequently combined in elementary chemistry courses.

The resonance structures in the VB model are particularly useful in predicting the effect of substituents on π systems such as benzene. They lead to the models of resonance structures for an electron-withdrawing group and electron-releasing group on benzene. The utility of MO theory is that a quantitative indication of the charge from the π system on an atom can be obtained from the squares of the weighting coefficient c_i on atom C_i. Charge q_i ≈ c_i². The reason for squaring the coefficient is that if an electron is described by an AO, then the square of the AO gives the electron density. The AOs are adjusted (normalized) so that AO² =1, and q_i ≈ (c_iAO_i)² ≈ c_i². In benzene, q_i = 1 on each C atom. With an electron-withdrawing group q_i < 1 on the ortho and para C atoms and > 1 for an electron-releasing group.

Coefficients

Weighting of the of resonance structures in terms of their contribution to the overall structure can be calculated in multiple ways, using "Ab initio" methods derived from Valence Bond theory, or else from the Natural Bond Orbitals (NBO) approaches of Weinhold NBO5, or finally from empirical calculations based on the Hückel method. A Hückel method-based software for teaching resonance is available on the HuLiS Web site.

History

The concept of resonance was introduced into quantum mechanics by Werner Heisenberg in 1926 in a discussion of the quantum states of the helium atom. He compared the structure of the helium atom with the classical system of resonating coupled harmonic oscillators. ^[4][12] Linus Pauling used this analogy to introduce his resonance theory in 1928. ^[13] In the classical system, the coupling produces two modes, one of which is lower in frequency than either of the uncoupled vibrations; quantum mechanically, this lower frequency is interpreted as a lower energy. The alternative term mesomerism popular in German and French publications with the same meaning was introduced by Christopher Ingold in 1938, but did not catch on in the English literature. The current concept of mesomeric effect has taken on a related but different meaning. The double headed arrow was introduced by the German chemist Fritz Arndt who preferred the German phrase zwischenstufe or intermediate stage.

In the Soviet Union, resonance theory — especially as developed by Linus Pauling — was attacked in the early 1950s as being contrary to the Marxist principles of dialectical materialism, and in June 1951 the Soviet Academy of Sciences under the leadership of Alexander Nesmeyanov convened a conference on the chemical structure of organic compounds, attended by 400 physicists, chemists, and philosophers, where "the pseudo-scientific essence of the theory of resonance was exposed and unmasked".^[14]

Due to confusion with the physical meaning of the word resonance, as no elements actually appear to be resonating, it has been suggested that the term resonance be abandoned in favor of delocalization.^[15] Resonance energy would become delocalization energy and a resonance structure becomes a contributing structure. The double headed arrows would be replaced by commas.

Representations

The ozone molecule is represented by two resonance structures. In reality the two terminal oxygen atoms are equivalent and the hybrid structure is drawn on the right with a charge of -1/2 on both oxygen atoms and partial double bonds with a full and dashed line and bond order 1.5.^[16][17]

In benzene the two cyclohexatriene Kekulé structures first proposed by Kekulé are taken together as contributing structures to represent the total structure. In the hybrid structure on the right the dashed hexagon replaces three double bonds, and represents six electrons in a set of three molecular orbitals of π symmetry, with a nodal plane in the plane of the molecule.

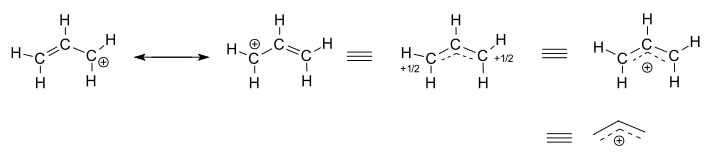
The allyl cation has two contributing structures with a positive charge on the terminal carbon atoms. In the hybrid structure their charge is +1/2. The full positive charge can also be depicted as delocalized among three carbon atoms.

In furan a lone pair of the oxygen atom interacts with the π orbitals of the carbon atoms. The curved arrows depicture the move of delocalized π electrons, which results in different contributors.

Reactive intermediates

Main article: Reactive intermediate

Often, reactive intermediates such as carbocations and free radicals have more delocalized structure than their parent reactants, giving rise to unexpected products. The classical example is allylic rearrangement. When 1 mole of HCl adds to 1 mole of 1,3-butadiene, in addition to the ordinarily expected product 3-chloro-1-butene, we also find 1-chloro-2-butene. Isotope labelling experiments have shown that what happens here is that the additional double bond shifts from 1,2 position to 2,3 position in some of the product. This and other evidence (such as NMR in superacid solutions) shows that the intermediate carbocation must have a highly delocalized structure, different from its mostly classical (delocalization exists but is small) parent molecule. This cation (an allylic cation) can be represented using resonance, as shown above.

This observation of greater delocalization in less stable molecules is quite general. The excited states of conjugated dienes are stabilised more by conjugation than their ground states, causing them to become organic dyes.

A well-studied example of delocalization that does not involve π electrons (hyperconjugation) can be observed in the non-classical ion norbornyl cation. Other examples are diborane and methanium (CH₅⁺). These can be viewed as containing 3-center-2-electron bonds and are represented either by contributing structures involving rearrangement of sigma electrons or by a special notation, a Y that has the three nuclei at its three points.

See also

• Aromaticity
• Conjugated system
• Delocalization
• Hyperconjugation
• Tautomerism
• Pi interaction

External links

• (French) N. Goudard, Y. Carissan, D. Hagebaum-Reignier, S. Humbel (2008). "HuLiS : Java Applet - Simple Hückel Theory and Mesomery - program logiciel software". http://www.hulis.free.fr. Retrieved 29 October 2010. 

References

1. ^ IUPAC Gold Book mesomerism PDF
2. ^ IUPAC Gold Book resonance PDF
3. ^ IUPAC Gold Book contributing structure PDF
4. ^ ^{a b c} Linus Pauling: The Nature of the chemical bond - An Introduction to Modern Structural Chemistry Cornell University Press, third Edition 1960, The Concept of Resonance, pp.10-13
5. ^ ^{a b} IUPAC Gold Book resonance energy PDF
6. ^ Linus Pauling: Resonance Manuscript for publication in Encyclopedia Britannica, p.13; July 29, 1946.
7. ^ Graphical representation for chemical structure diagrams (IUPAC Recommendations 2008) GR-8, p.387
8. ^ Graphical representation for chemical structure diagrams (IUPAC Recommendations 2008) GR-6, pp.379-382
9. ^ Robert Morrison, Robert Boyd (1989). "Chapter 10". Organic Chemistry (Fifth Edition ed.). Prentice Hall of India. pp. 372. ISBN 0-87692-560-3. "The resonance hybrid is more stable than any of the contributing structures." 
10. ^ Wiberg, Nakaji and Morgan Heat of hydrogenation of a cis imine. An experimental and theoretical study J. Am. Chem. Soc., 1993, 115 (9), pp 3527–3532; doi:10.1021/ja00062a017
11. ^ J. Sherman The heats of hydrogenation of unsaturated hydrocarbons. Journal of the American Oil Chemists' Society; Volume 16, Number 2; February, 1939; doi:10.1007/BF02543208
12. ^ Linus Pauling: Resonance p.1
13. ^ The Science and Humanism of Linus Pauling. See last paragraph of section 1.
14. ^ Terror and Progress USSR: Some Sources of Change and Stability in the Soviet Dictatorship by Barrington Moore, Jr. (1954), pp. 142-143.
15. ^ If It's Resonance, What Is Resonating? Kerber, Robert C. . J. Chem. Educ. 2006 83 223. Abstract
16. ^ Organic Chemistry (6th Edition) L. G. Wade
17. ^ Organic Chemistry (4th Edition) Paula Y. Bruice