Nash equilibrium

Nash Equilibrium
A solution concept in game theory
Relationships
Subset of	Rationalizability, Epsilon-equilibrium, Correlated equilibrium
Superset of	Evolutionarily stable strategy, Subgame perfect equilibrium, Perfect Bayesian equilibrium, Trembling hand perfect equilibrium, Stable Nash equilibrium, Strong Nash equilibrium
Significance
Proposed by	John Forbes Nash
Used for	All non-cooperative games
Example	Rock paper scissors

In game theory, Nash equilibrium (named after John Forbes Nash, who proposed it) is a solution concept of a game involving two or more players, in which each player is assumed to know the equilibrium strategies of the other players, and no player has anything to gain by changing only his own strategy unilaterally. If each player has chosen a strategy and no player can benefit by changing his or her strategy while the other players keep theirs unchanged, then the current set of strategy choices and the corresponding payoffs constitute a Nash equilibrium.

Stated simply, Amy and Phil are in Nash equilibrium if Amy is making the best decision she can, taking into account Phil's decision, and Phil is making the best decision he can, taking into account Amy's decision. Likewise, a group of players is in Nash equilibrium if each one is making the best decision that he or she can, taking into account the decisions of the others. However, Nash equilibrium does not necessarily mean the best payoff for all the players involved; in many cases, all the players might improve their payoffs if they could somehow agree on strategies different from the Nash equilibrium: e.g., competing businesses forming a cartel in order to increase their profits.

Applications

Game theorists use the Nash equilibrium concept to analyze the outcome of the strategic interaction of several decision makers. In other words, it provides a way of predicting what will happen if several people or several institutions are making decisions at the same time, and if the outcome depends on the decisions of the others. The simple insight underlying John Nash's idea is that we cannot predict the result of the choices of multiple decision makers if we analyze those decisions in isolation. Instead, we must ask what each player would do, taking into account the decision-making of the others.

Nash equilibrium has been used to analyze hostile situations like war and arms races^[1] (see Prisoner's dilemma), and also how conflict may be mitigated by repeated interaction (see Tit-for-tat). It has also been used to study to what extent people with different preferences can cooperate (see Battle of the sexes), and whether they will take risks to achieve a cooperative outcome (see Stag hunt). It has been used to study the adoption of technical standards, and also the occurrence of bank runs and currency crises (see Coordination game). Other applications include traffic flow (see Wardrop's principle), how to organize auctions (see auction theory), the outcome of efforts exerted by multiple parties in the education process,^[2] and even penalty kicks in soccer (see Matching pennies).^[3]

History

A version of the Nash equilibrium concept was first used by Antoine Augustin Cournot in his theory of oligopoly (1838). In Cournot's theory, firms choose how much output to produce to maximize their own profit. However, the best output for one firm depends on the outputs of others. A Cournot equilibrium occurs when each firm's output maximizes its profits given the output of the other firms, which is a pure strategy Nash Equilibrium.

The modern game-theoretic concept of Nash Equilibrium is instead defined in terms of mixed strategies, where players choose a probability distribution over possible actions. The concept of the mixed strategy Nash Equilibrium was introduced by John von Neumann and Oskar Morgenstern in their 1944 book The Theory of Games and Economic Behavior. However, their analysis was restricted to the special case of zero-sum games. They showed that a mixed-strategy Nash Equilibrium will exist for any zero-sum game with a finite set of actions. The contribution of John Forbes Nash in his 1951 article Non-Cooperative Games was to define a mixed strategy Nash Equilibrium for any game with a finite set of actions and prove that at least one (mixed strategy) Nash Equilibrium must exist in such a game.

Since the development of the Nash equilibrium concept, game theorists have discovered that it makes misleading predictions (or fails to make a unique prediction) in certain circumstances. Therefore they have proposed many related solution concepts (also called 'refinements' of Nash equilibrium) designed to overcome perceived flaws in the Nash concept. One particularly important issue is that some Nash equilibria may be based on threats that are not 'credible'. Therefore, in 1965 Reinhard Selten proposed subgame perfect equilibrium as a refinement that eliminates equilibria which depend on non-credible threats. Other extensions of the Nash equilibrium concept have addressed what happens if a game is repeated, or what happens if a game is played in the absence of perfect information. However, subsequent refinements and extensions of the Nash equilibrium concept share the main insight on which Nash's concept rests: all equilibrium concepts analyze what choices will be made when each player takes into account the decision-making of others.

Definitions

Informal definition

Informally, a set of strategies is a Nash equilibrium if no player can do better by unilaterally changing his or her strategy. To see what this means, imagine that each player is told the strategies of the others. Suppose then that each player asks himself or herself: "Knowing the strategies of the other players, and treating the strategies of the other players as set in stone, can I benefit by changing my strategy?"

If any player would answer "Yes", then that set of strategies is not a Nash equilibrium. But if every player prefers not to switch (or is indifferent between switching and not) then the set of strategies is a Nash equilibrium. Thus, each strategy in a Nash equilibrium is a best response to all other strategies in that equilibrium.^[4]

The Nash equilibrium may sometimes appear non-rational in a third-person perspective. This is because it may happen that a Nash equilibrium is not Pareto optimal.

The Nash equilibrium may also have non-rational consequences in sequential games because players may "threaten" each other with non-rational moves. For such games the subgame perfect Nash equilibrium may be more meaningful as a tool of analysis.

Formal definition

Let (S, f) be a game with n players, where S_i is the strategy set for player i, S=S₁ X S₂ ... X S_n is the set of strategy profiles and f=(f₁(x), ..., f_n(x)) is the payoff function for x $\in$ S. Let x_i be a strategy profile of player i and x_-i be a strategy profile of all players except for player i. When each player i $\in$ {1, ..., n} chooses strategy x_i resulting in strategy profile x = (x₁, ..., x_n) then player i obtains payoff f_i(x). Note that the payoff depends on the strategy profile chosen, i.e., on the strategy chosen by player i as well as the strategies chosen by all the other players. A strategy profile x^* $\in$ S is a Nash equilibrium (NE) if no unilateral deviation in strategy by any single player is profitable for that player, that is

$\forall i,x_i\in S_i, x_i \neq x^*_{i} : f_i(x^*_{i}, x^*_{-i}) \geq f_i(x_{i},x^*_{-i}).$

A game can have either a pure-strategy or a mixed Nash Equilibrium, (in the latter a pure strategy is chosen stochastically with a fixed frequency). Nash proved that if we allow mixed strategies, then every game with a finite number of players in which each player can choose from finitely many pure strategies has at least one Nash equilibrium.

When the inequality above holds strictly (with > instead of $\geq$) for all players and all feasible alternative strategies, then the equilibrium is classified as a strict Nash equilibrium. If instead, for some player, there is exact equality between $x^*_i$ and some other strategy in the set S, then the equilibrium is classified as a weak Nash equilibrium.

Examples

Coordination game

Main article: Coordination game

A sample coordination game showing relative payoff for player1 / player2 with each combination

	Player 2 adopts strategy A	Player 2 adopts strategy B
Player 1 adopts strategy A	4, 4	1, 3
Player 1 adopts strategy B	3, 1	3, 3

The coordination game is a classic (symmetric) two player, two strategy game, with an example payoff matrix shown to the right. The players should thus coordinate, both adopting strategy A, to receive the highest payoff; i.e., 4. If both players chose strategy B though, there is still a Nash equilibrium. Although each player is awarded less than optimal payoff, neither player has incentive to change strategy due to a reduction in the immediate payoff (from 3 to 1).

An example of a coordination game is the setting where two technologies are available to two firms with compatible products, and they have to elect a strategy to become the market standard. If both firms agree on the chosen technology, high sales are expected for both firms. If the firms do not agree on the standard technology, few sales result. Both strategies are Nash equilibria of the game.

Driving on a road, and having to choose either to drive on the left or to drive on the right of the road, is also a coordination game. For example, with payoffs 100 meaning no crash and 0 meaning a crash, the coordination game can be defined with the following payoff matrix:

The driving game

	Drive on the Left	Drive on the Right
Drive on the Left	100, 100	0, 0
Drive on the Right	0, 0	100, 100

In this case there are two pure strategy Nash equilibria, when both choose to either drive on the left or on the right. If we admit mixed strategies (where a pure strategy is chosen at random, subject to some fixed probability), then there are three Nash equilibria for the same case: two we have seen from the pure-strategy form, where the probabilities are (0%,100%) for player one, (0%, 100%) for player two; and (100%, 0%) for player one, (100%, 0%) for player two respectively. We add another where the probabilities for each player is (50%, 50%).

Prisoner's dilemma

Main article: Prisoner's dilemma

(note differences in the orientation of the payoff matrix)

Example PD payoff matrix

	Cooperate	Defect
Cooperate	3, 3	0, 5
Defect	5, 0	1, 1

The Prisoner's Dilemma has the same payoff matrix as depicted for the Coordination Game, but now C > A > D > B. Because C > A and D > B, each player improves his situation by switching from strategy #1 to strategy #2, no matter what the other player decides. The Prisoner's Dilemma thus has a single Nash Equilibrium: both players choosing strategy #2 ("defect"). What has long made this an interesting case to study is the fact that D < A (i.e., "both defect" is globally inferior to "both remain loyal"). The globally optimal strategy is unstable; it is not an equilibrium.

Network traffic

See also: Braess's Paradox

Sample network graph. Values on edges are the travel time experienced by a 'car' travelling down that edge. x is the number of cars travelling via that edge.

An application of Nash equilibria is in determining the expected flow of traffic in a network. Consider the graph on the right. If we assume that there are x "cars" traveling from A to D, what is the expected distribution of traffic in the network?

This situation can be modeled as a "game" where every traveler has a choice of 3 strategies, where each strategy is a route from A to D (either ABD, ABCD, or ACD). The "payoff" of each strategy is the travel time of each route. In the graph on the right, a car travelling via ABD experiences travel time of (1 + x / 100) + 2, where x is the number of cars traveling on edge AB. Thus, payoffs for any given strategy depend on the choices of the other players, as is usual. However, the goal in this case is to minimize travel time, not maximize it. Equilibrium will occur when the time on all paths is exactly the same. When that happens, no single driver has any incentive to switch routes, since it can only add to his/her travel time. For the graph on the right, if, for example, 100 cars are travelling from A to D, then equilibrium will occur when 25 drivers travel via ABD, 50 via ABCD, and 25 via ACD. Every driver now has a total travel time of 3.75.

Notice that this distribution is not, actually, socially optimal. If the 100 cars agreed that 50 travel via ABD and the other 50 through ACD, then travel time for any single car would actually be 3.5 which is less than 3.75. This is also the Nash equilibrium if the path between B and C is removed, which means that adding an additional possible route can decrease the efficiency of the system, a phenomenon known as Braess's Paradox.

Competition game

A competition game

	Player 2 chooses '0'	Player 2 chooses '1'	Player 2 chooses '2'	Player 2 chooses '3'
Player 1 chooses '0'	0, 0	2, -2	2, -2	2, -2
Player 1 chooses '1'	-2, 2	1, 1	3, -1	3, -1
Player 1 chooses '2'	-2, 2	-1, 3	2, 2	4, 0
Player 1 chooses '3'	-2, 2	-1, 3	0, 4	3, 3

This can be illustrated by a two-player game in which both players simultaneously choose an integer from 0 to 3 and they both win the smaller of the two numbers in points. In addition, if one player chooses a larger number than the other, then he/she has to give up two points to the other.

This game has a unique pure-strategy Nash equilibrium: both players choosing 0 (highlighted in light red). Any other choice of strategies can be improved if one of the players lowers his number to one less than the other player's number. In the table to the right, for example, when starting at the green square it is in player 1's interest to move to the purple square by choosing a smaller number, and it is in player 2's interest to move to the blue square by choosing a smaller number. If the game is modified so that the two players win the named amount if they both choose the same number, and otherwise win nothing, then there are 4 Nash equilibria (0,0...1,1...2,2...and 3,3).

Nash equilibria in a payoff matrix

There is an easy numerical way to identify Nash equilibria on a payoff matrix. It is especially helpful in two-person games where players have more than two strategies. In this case formal analysis may become too long. This rule does not apply to the case where mixed (stochastic) strategies are of interest. The rule goes as follows: if the first payoff number, in the duplet of the cell, is the maximum of the column of the cell and if the second number is the maximum of the row of the cell - then the cell represents a Nash equilibrium.

A Payoff Matrix - Nash Equlibria in bold

	Option A	Option B	Option C
Option A	0, 0	25, 40	5, 10
Option B	40, 25	0, 0	5, 15
Option C	10, 5	15, 5	10, 10

We can apply this rule to a 3×3 matrix:

Using the rule, we can very quickly (much faster than with formal analysis) see that the Nash Equlibria cells are (B,A), (A,B), and (C,C). Indeed, for cell (B,A) 40 is the maximum of the first column and 25 is the maximum of the second row. For (A,B) 25 is the maximum of the second column and 40 is the maximum of the first row. Same for cell (C,C). For other cells, either one or both of the duplet members are not the maximum of the corresponding rows and columns.

This said, the actual mechanics of finding equilibrium cells is obvious: find the maximum of a column and check if the second member of the pair is the maximum of the row. If these conditions are met, the cell represents a Nash Equilibrium. Check all columns this way to find all NE cells. An N×N matrix may have between 0 and N×N pure strategy Nash equilibria.

Stability

The concept of stability, useful in the analysis of many kinds of equilibria, can also be applied to Nash equilibria.

A Nash equilibrium for a mixed strategy game is stable if a small change (specifically, an infinitesimal change) in probabilities for one player leads to a situation where two conditions hold:

1. the player who did not change has no better strategy in the new circumstance
2. the player who did change is now playing with a strictly worse strategy.

If these cases are both met, then a player with the small change in his mixed-strategy will return immediately to the Nash equilibrium. The equilibrium is said to be stable. If condition one does not hold then the equilibrium is unstable. If only condition one holds then there are likely to be an infinite number of optimal strategies for the player who changed. John Nash showed that the latter situation could not arise in a range of well-defined games.

In the "driving game" example above there are both stable and unstable equilibria. The equilibria involving mixed-strategies with 100% probabilities are stable. If either player changes his probabilities slightly, they will be both at a disadvantage, and his opponent will have no reason to change his strategy in turn. The (50%,50%) equilibrium is unstable. If either player changes his probabilities, then the other player immediately has a better strategy at either (0%, 100%) or (100%, 0%).

Stability is crucial in practical applications of Nash equilibria, since the mixed-strategy of each player is not perfectly known, but has to be inferred from statistical distribution of his actions in the game. In this case unstable equilibria are very unlikely to arise in practice, since any minute change in the proportions of each strategy seen will lead to a change in strategy and the breakdown of the equilibrium.

The Nash equilibrium defines stability only in terms of unilateral deviations. In cooperative games such a concept is not convincing enough. Strong Nash equilibrium allows for deviations by every conceivable coalition.^[5] Formally, a Strong Nash equilibrium is a Nash equilibrium in which no coalition, taking the actions of its complements as given, can cooperatively deviate in a way that benefits all of its members.^[6] However, the Strong Nash concept is sometimes perceived as too "strong" in that the environment allows for unlimited private communication. In fact, Strong Nash equilibrium has to be Pareto efficient. As a result of these requirements, Strong Nash almost never exists.

A refined Nash equilibrium known as coalition-proof Nash equilibrium (CPNE)^[5] occurs when players cannot do better even if they are allowed to communicate and make "self-enforcing" agreement to deviate. Every correlated strategy supported by iterated strict dominance and on the Pareto frontier is a CPNE.^[7] Further, it is possible for a game to have a Nash equilibrium that is resilient against coalitions less than a specified size, k. CPNE is related to the theory of the core.

Occurrence

If a game has a unique Nash equilibrium and is played among players under certain conditions, then the NE strategy set will be adopted. Sufficient conditions to guarantee that the Nash equilibrium is played are:

1. The players all will do their utmost to maximize their expected payoff as described by the game.
2. The players are flawless in execution.
3. The players have sufficient intelligence to deduce the solution.
4. The players know the planned equilibrium strategy of all of the other players.
5. The players believe that a deviation in their own strategy will not cause deviations by any other players.
6. There is common knowledge that all players meet these conditions, including this one. So, not only must each player know the other players meet the conditions, but also they must know that they all know that they meet them, and know that they know that they know that they meet them, and so on.

Where the conditions are not met

Examples of game theory problems in which these conditions are not met:

1. The first condition is not met if the game does not correctly describe the quantities a player wishes to maximize. In this case there is no particular reason for that player to adopt an equilibrium strategy. For instance, the prisoner’s dilemma is not a dilemma if either player is happy to be jailed indefinitely.
2. Intentional or accidental imperfection in execution. For example, a computer capable of flawless logical play facing a second flawless computer will result in equilibrium. Introduction of imperfection will lead to its disruption either through loss to the player who makes the mistake, or through negation of the common knowledge criterion leading to possible victory for the player. (An example would be a player suddenly putting the car into reverse in the game of chicken, ensuring a no-loss no-win scenario).
3. In many cases, the third condition is not met because, even though the equilibrium must exist, it is unknown due to the complexity of the game, for instance in Chinese chess.^[8] Or, if known, it may not be known to all players, as when playing tic-tac-toe with a small child who desperately wants to win (meeting the other criteria).
4. The criterion of common knowledge may not be met even if all players do, in fact, meet all the other criteria. Players wrongly distrusting each other's rationality may adopt counter-strategies to expected irrational play on their opponents’ behalf. This is a major consideration in “Chicken” or an arms race, for example.

Where the conditions are met

Due to the limited conditions in which NE can actually be observed, they are rarely treated as a guide to day-to-day behaviour, or observed in practice in human negotiations. However, as a theoretical concept in economics and evolutionary biology, the NE has explanatory power. The payoff in economics is utility (or sometimes money), and in evolutionary biology gene transmission, both are the fundamental bottom line of survival. Researchers who apply games theory in these fields claim that strategies failing to maximize these for whatever reason will be competed out of the market or environment, which are ascribed the ability to test all strategies. This conclusion is drawn from the "stability" theory above. In these situations the assumption that the strategy observed is actually a NE has often been borne out by research^{[citation needed]}.^{[verification needed]}

NE and non-credible threats

Extensive and Normal form illustrations that show the difference between SPNE and other NE. The blue equilibrium is not subgame perfect because player two makes a non-credible threat at 2(2) to be unkind (U).

The Nash equilibrium is a superset of the subgame perfect Nash equilibrium. The subgame perfect equilibrium in addition to the Nash Equilibrium requires that the strategy also is a Nash equilibrium in every subgame of that game. This eliminates all non-credible threats, that is, strategies that contain non-rational moves in order to make the counter-player change his strategy.

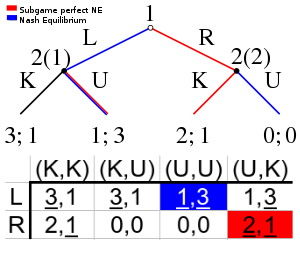
The image to the right shows a simple sequential game that illustrates the issue with subgame imperfect Nash equilibria. In this game player one chooses left(L) or right(R), which is followed by player two being called upon to be kind (K) or unkind (U) to player one, However, player two only stands to gain from being unkind if player one goes left. If player one goes right the rational player two would de facto be kind to him in that subgame. However, The non-credible threat of being unkind at 2(2) is still part of the blue (L, (U,U)) Nash equilibrium. Therefore, if rational behavior can be expected by both parties the subgame perfect Nash equilibrium may be a more meaningful solution concept when such dynamic inconsistencies arise.

Proof of existence

Proof using the Kakutani fixed point theorem

Nash's original proof (in his thesis) used Brouwer's fixed point theorem (e.g., see below for a variant). We give a simpler proof via the Kakutani fixed point theorem, following Nash's 1950 paper (he credits David Gale with the observation that such a simplification is possible).

To prove the existence of a Nash Equilibrium, let r_i(σ _{− i}) be the best response of player i to the strategies of all other players.

$r_i = \arg\max_{\sigma_i} u_i (\sigma_i,\sigma_{-i})$

Here, $\sigma \in \Sigma$ is a mixed strategy profile in the set of all mixed strategies and u_i it the payoff function for player i. Define a function r = (r_i,r _{− i}) such that $r: \Sigma \rightarrow \Sigma$. The existence of a Nash Equilibrium is equivalent to r having a fixed point.

Kakutani's fixed point theorem guarantees the existence of a fixed point if the following four conditions are satisfied.

1. Σ is compact, convex, and nonempty.
2. r(σ) is nonempty.
3. r(σ) is convex.
4. r(σ)is upper hemicontinuous

Condition 1. is satisfied from the fact that Σ is a simplex and thus compact. Convexity follows from players' ability to mix strategies. Σ is nonempty as long as players have strategies.

Condition 2. is satisfied because players maximize expected payoffs which is continuous function over a compact set. The Weierstrauss Extreme Value Theorem guarantees that there is always a maximum value.

Condition 3. is satisfied as a result of mixed strategies. Suppose $\sigma_i, \sigma'_i \in r(\sigma_{-i})$, then $\lambda \sigma_i + (1-\lambda) \sigma'_i \in r(\sigma_{-i})$. i.e. if two strategies maximize payoffs, then a mix between the two strategies will yield the same payoff.

Condition 4. is satisfied by way of Berge's Maximum Theorem. Because u_i is continuos and compact, r(σ_i) is upper hemicontinuous.

Therefore, there exists a fixed point in r and a Nash Equilibrium.^[9]

When Nash made this point to John von Neumann in 1949, von Neumann famously dismissed it with the words, "That's trivial, you know. That's just a fixed point theorem." (See Nasar, 1998, p. 94.)

Alternate proof using the Brouwer fixed-point theorem

We have a game G = (N,A,u) where N is the number of players and $A = A_1 \times \ldots \times A_N$ is the action set for the players. All of the action sets A_i are finite. Let $\Delta = \Delta_1 \times \ldots \times \Delta_N$ denote the set of mixed strategies for the players. The finiteness of the A_is ensures the compactness of Δ.

We can now define the gain functions. For a mixed strategy $\sigma \in \Delta$, we let the gain for player i on action $a \in A_i$ be

$\text{Gain}_i(\sigma,a) = \max \{0, u_i(a_i, \sigma_{-i}) - u_i(\sigma_{i}, \sigma_{-i})\}.\$

The gain function represents the benefit a player gets by unilaterally changing his strategy. We now define $g = (g_1,\ldots,g_N)$ where

$g_i(\sigma)(a) = \sigma_i(a) + \text{Gain}_i(\sigma,a)\$

for $\sigma \in \Delta, a \in A_i$. We see that

$\sum_{a \in A_i} g_i(\sigma)(a) = \sum_{a \in A_i} \sigma_i(a) + \text{Gain}_i(\sigma,a) = 1 + \sum_{a \in A_i} \text{Gain}_i(\sigma,a) > 0.\$

We now use g to define $f: \Delta \rightarrow \Delta$ as follows. Let

$f_i(\sigma)(a) = \frac{g_i(\sigma)(a)}{\sum_{b \in A_i} g_i(\sigma)(b)}$

for $a \in A_i$. It is easy to see that each f_i is a valid mixed strategy in Δ_i. It is also easy to check that each f_i is a continuous function of σ, and hence f is a continuous function. Now Δ is the cross product of a finite number of compact convex sets, and so we get that Δ is also compact and convex. Therefore we may apply the Brouwer fixed point theorem to f. So f has a fixed point in Δ, call it σ ^* .

I claim that σ ^* is a Nash Equilibrium in G. For this purpose, it suffices to show that

$\forall 1 \leq i \leq N, ~ \forall a \in A_i, ~ \text{Gain}_i(\sigma^*,a) = 0 \text{.}$

This simply states the each player gains no benefit by unilaterally changing his strategy which is exactly the necessary condition for being a Nash Equilibrium.

Now assume that the gains are not all zero. Therefore, $\exists i$, $1 \leq i \leq N$, and $a \in A_i$ such that Gain_i(σ ^* ,a) > 0. Note then that

$\sum_{a \in A_i} g_i(\sigma^*, a) = 1 + \sum_{a \in A_i} Gain_i(\sigma^*,a) > 1.$

So let $C = \sum_{a \in A_i} g_i(\sigma^*, a)$. Also we shall denote $\text{Gain}(i,\cdot)$ as the gain vector indexed by actions in A_i. Since f(σ ^* ) = σ ^* we clearly have that $f_i(\sigma^*) = \sigma^*_i$. Therefore we see that

$\sigma^*_i = \frac{g_i(\sigma^*)}{\sum_{a \in A_i} g_i(\sigma^*)(a)} \Rightarrow \sigma^*_i = \frac{\sigma^*_i + \text{Gain}_i(\sigma^*,\cdot)}{C} \Rightarrow C\sigma^*_i = \sigma^*_i + \text{Gain}_i(\sigma^*,\cdot)$

$\left(C-1\right)\sigma^*_i = \text{Gain}_i(\sigma^*,\cdot) \Rightarrow \sigma^*_i = \left(\frac{1}{C-1}\right)\text{Gain}_i(\sigma^*,\cdot).$

Since C > 1 we have that $\sigma^*_i$ is some positive scaling of the vector $\text{Gain}_i(\sigma^*,\cdot)$. Now I claim that

$\sigma^*_i(a)(u_i(a_i, \sigma^*_{-i}) - u_i(\sigma^*_i, \sigma^*_{-i})) = \sigma^*_i(a)\text{Gain}_i(\sigma^*, a)$

$\forall a \in A_i$. To see this, we first note that if Gain_i(σ ^* ,a) > 0 then this is true by definition of the gain function. Now assume that Gain_i(σ ^* ,a) = 0. By our previous statements we have that

$\sigma^*_i(a) = \left(\frac{1}{C-1}\right)\text{Gain}_i(\sigma^*, a) = 0$

and so the left term is zero, giving us that the entire expression is 0 as needed.

So we finally have that

$0 = u_i(\sigma^*_i, \sigma^*_{-i}) - u_i(\sigma^*_i, \sigma^*_{-i})$

$= \left(\sum_{a \in A_i} \sigma^*_i(a)u_i(a_i, \sigma^*_{-i})\right) - u_i(\sigma^*_i, \sigma^*_{-i})$

$= \sum_{a \in A_i} \sigma^*_i(a) (u_i(a_i, \sigma^*_{-i}) - u_i(\sigma^*_i, \sigma^*_{-i}))$

$= \sum_{a \in A_i} \sigma^*_i(a) \text{Gain}_i(\sigma^*, a) \quad \text{ by the previous statements }$

$= \sum_{a \in A_i} \left( C -1 \right) \sigma^*_i(a)^2 > 0$

where the last inequality follows since $\sigma^*_i$ is a non-zero vector. But this is a clear contradiction, so all the gains must indeed be zero. Therefore σ ^* is a Nash Equilibrium for G as needed.

Computing Nash equilibria

If a player A has a dominant strategy s_A then there exists a Nash equilibrium in which A plays s_A. In the case of two players A and B, there exists a Nash equilibrium in which A plays s_A and B plays a best response to s_A. If s_A is a strictly dominant strategy, A plays s_A in all Nash equilibria. If both A and B have strictly dominant strategies, there exists a unique Nash equilibrium in which each plays his strictly dominant strategy.

In games with mixed strategy Nash equilibria, the probability of a player choosing any particular strategy can be computed by assigning a variable to each strategy that represents a fixed probability for choosing that strategy. In order for a player to be willing to randomize, his expected payoff for each strategy should be the same. In addition, the sum of the probabilities for each strategy of a particular player should be 1. This creates a system of equations from which the probabilities of choosing each strategy can be derived.^[4]

Examples

Matching pennies

	Player B plays H	Player B plays T
Player A plays H	−1, +1	+1, −1
Player A plays T	+1, −1	−1, +1

In the matching pennies game, player A loses a point to B if A and B play the same strategy and wins a point from B if they play different strategies. To compute the mixed strategy Nash equilibrium, assign A the probability p of playing H and (1−p) of playing T, and assign B the probability q of playing H and (1−q) of playing T.

E[payoff for A playing H] = (−1)q + (+1)(1−q) = 1−2q

E[payoff for A playing T] = (+1)q + (−1)(1−q) = 2q−1

E[payoff for A playing H] = E[payoff for A playing T] ⇒ 1−2q = 2q−1 ⇒ q = 1/2

E[payoff for B playing H] = (+1)p + (−1)(1−p) = 2p−1

E[payoff for B playing T] = (−1)p + (+1)(1−p) = 1−2p

E[payoff for B playing H] = E[payoff for B playing T] ⇒ 2p−1 = 1−2p ⇒ p = 1/2

Thus a mixed strategy Nash equilibrium in this game is for each player to randomly choose H or T with equal probability.

See also

• Adjusted winner procedure
• Best response
• Braess's paradox
• Complementarity theory
• Conflict resolution research
• Cooperation
• Evolutionarily stable strategy
• Game theory
• Glossary of game theory
• Hotelling's law
• Mexican Standoff
• Minimax theorem
• Optimum contract and par contract
• Prisoner's dilemma
• Relations between equilibrium concepts
• Self-confirming equilibrium
• Solution concept
• Equilibrium selection
• Stackelberg competition
• Subgame perfect Nash equilibrium
• Wardrop's principle

Notes

1. ^ Schelling, Thomas, The Strategy of Conflict, copyright 1960, 1980, Harvard University Press, ISBN 0674840313.
2. ^ G. De Fraja, T. Oliveira, L. Zanchi (2010), 'Must Try Harder: Evaluating the Role of Effort in Educational Attainment'. "The Review of Economis and Statistics" 92:3. pp. 577-597
3. ^ P. Chiappori, S. Levitt, and T. Groseclose (2002), 'Testing Mixed-Strategy Equilibria When Players Are Heterogeneous: The Case of Penalty Kicks in Soccer'. American Economic Review 92, pp. 1138-51.
4. ^ ^{a b} von Ahn, Luis. "Preliminaries of Game Theory". http://www.scienceoftheweb.org/15-396/lectures_f11/lecture08.pdf. Retrieved 2008-11-07. 
5. ^ ^{a b} B. D. Bernheim, B. Peleg, M. D. Whinston (1987), "Coalition-Proof Equilibria I. Concepts", Journal of Economic Theory 42 (1): 1–12, doi:10.1016/0022-0531(87)90099-8. 
6. ^ R. Aumann, (1959), Acceptable points in general cooperative n-person games in "Contributions to the Theory of Games IV", Princeton Univ. Press, Princeton, N.J.. 
7. ^ D. Moreno, J. Wooders (1996), "Coalition-Proof Equilibrium", Games and Economic Behavior 17 (1): 80–112, doi:10.1006/game.1996.0095. 
8. ^ Nash proved that a perfect NE exists for this type of finite extensive form game^{[citation needed]} – it can be represented as a strategy complying with his original conditions for a game with a NE. Such games may not have unique NE, but at least one of the many equilibrium strategies would be played by hypothetical players having perfect knowledge of all 10¹⁵⁰ game trees^{[citation needed]}.
9. ^ Fudenburg, Drew, and Jean Tirole. Game Theory: Massachusetts Institute of Technology, 1991.

References

Game theory textbooks

• Dixit, Avinash and Susan Skeath. Games of Strategy. W.W. Norton & Company. (Second edition in 2004)
• Dutta, Prajit K. (1999), Strategies and games: theory and practice, MIT Press, ISBN 978-0-262-04169-0 . Suitable for undergraduate and business students.
• Fudenberg, Drew and Jean Tirole (1991) Game Theory MIT Press.
• Leyton-Brown, Kevin; Shoham, Yoav (2008), Essentials of Game Theory: A Concise, Multidisciplinary Introduction, San Rafael, CA: Morgan & Claypool Publishers, ISBN 978-1-598-29593-1, http://www.gtessentials.org . An 88-page mathematical introduction; see Chapter 2. Free online at many universities.
• Morgenstern, Oskar and John von Neumann (1947) The Theory of Games and Economic Behavior Princeton University Press
• Myerson, Roger B. (1997), Game theory: analysis of conflict, Harvard University Press, ISBN 978-0-674-34116-6 
• Rubinstein, Ariel; Osborne, Martin J. (1994), A course in game theory, MIT Press, ISBN 978-0-262-65040-3 . A modern introduction at the graduate level.
• Shoham, Yoav; Leyton-Brown, Kevin (2009), Multiagent Systems: Algorithmic, Game-Theoretic, and Logical Foundations, New York: Cambridge University Press, ISBN 978-0-521-89943-7, http://www.masfoundations.org . A comprehensive reference from a computational perspective; see Chapter 3. Downloadable free online.
• Gibbons, Robert (1992), Game Theory for Applied Economists, Princeton University Press (July 13, 1992), ISBN 978-0-691-00395-5 . Lucid and detailed introduction to game theory in an explicitly economic context.
• Osborne, Martin, An introduction to game theory, Oxford University . Introduction to Nash equilibrium.

Original Nash papers

• Nash, John (1950) "Equilibrium points in n-person games" Proceedings of the National Academy of Sciences 36(1):48-49.
• Nash, John (1951) "Non-Cooperative Games" The Annals of Mathematics 54(2):286-295.

Other references

• Mehlmann, A. The Game's Afoot! Game Theory in Myth and Paradox, American Mathematical Society (2000).
• Nasar, Sylvia (1998), "A Beautiful Mind", Simon and Schuster, Inc.

External links

• Complete Proof of Existence of Nash Equilibria