Normal-form game

In game theory, normal form is a way of describing a game. Unlike extensive form, normal-form representations are not graphical per se, but rather represent the game by way of a matrix. While this approach can be of greater use in identifying strictly dominated strategies and Nash equilibria, some information is lost as compared to extensive-form representations. The normal-form representation of a game includes all perceptible and conceivable strategies, and their corresponding payoffs, of each player.

In static games of complete, perfect information, a normal-form representation of a game is a specification of players' strategy spaces and payoff functions. A strategy space for a player is the set of all strategies available to that player, where a strategy is a complete plan of action for every stage of the game, regardless of whether that stage actually arises in play. A payoff function for a player is a mapping from the cross-product of players' strategy spaces to that player's set of payoffs (normally the set of real numbers, where the number represents a cardinal or ordinal utility—often cardinal in the normal-form representation) of a player, i.e. the payoff function of a player takes as its input a strategy profile (that is a specification of strategies for every player) and yields a representation of payoff as its output.

An example

A normal-form game

Player 1 \ Player 2	Player 2 chooses left	Player 2 chooses right
Player 1 chooses top	4, 3	−1, −1
Player 1 chooses bottom	0, 0	3, 4

The matrix to the right is a normal-form representation of a game in which players move simultaneously (or at least do not observe the other player's move before making their own) and receive the payoffs as specified for the combinations of actions played. For example, if player 1 plays top and player 2 plays left, player 1 receives 4 and player 2 receives 3. In each cell, the first number represents the payoff to the row player (in this case player 1), and the second number represents the payoff to the column player (in this case player 2).

Other representations

Often symmetric games (where the payoffs do not depend on which player chooses each action) are represented with only one payoff. This is the payoff for the row player. For example, the payoff matrices on the right and left below represent the same game.

Both players Stag Hare Stag 3, 3 0, 2 Hare 2, 0 2, 2

Just row Stag Hare Stag 3 0 Hare 2 2

Uses of normal form

Dominated strategies

The Prisoner's Dilemma

	Cooperate	Defect
Cooperate	−1, −1	−5, 0
Defect	0, −5	−2, −2

The payoff matrix facilitates elimination of dominated strategies, and it is usually used to illustrate this concept. For example, in the prisoner's dilemma (to the right), we can see that each prisoner can either "cooperate" or "defect". If exactly one prisoner defects, he gets off easily and the other prisoner is locked up for good. However, if they both defect, they will both be locked up for longer. One can determine that Cooperate is strictly dominated by Defect. One must compare the first numbers in each column, in this case 0 > −1 and −2 > −5. This shows that no matter what the column player chooses, the row player does better by choosing Defect. Similarly, one compares the second payoff in each row; again 0 > −1 and −2 > −5. This shows that no matter what row does, column does better by choosing Defect. This demonstrates the unique Nash equilibrium of this game is (Defect, Defect).

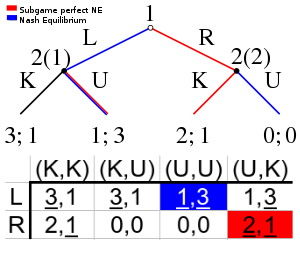
Sequential games in normal form

Both extensive and normal form illustration of a sequential form game with subgame imperfect and perfect Nash equilibriium marked with red and blue respectively.

A sequential game

	Left, Left	Left, Right	Right, Left	Right, Right
Top	4, 3	4, 3	−1, −1	−1, −1
Bottom	0, 0	3, 4	0, 0	3, 4

These matrices only represent games in which moves are simultaneous (or, more generally, information is imperfect). The above matrix does not represent the game in which player 1 moves first, observed by player 2, and then player 2 moves, because it does not specify each of player 2's strategies in this case. In order to represent this sequential game we must specify all of player 2's actions, even in contingencies that can never arise in the course of the game. In this game, player 2 has actions, as before, Left and Right. Unlike before he has four strategies, contingent on player 1's actions. The strategies are:

1. Left if player 1 plays Top and Left otherwise
2. Left if player 1 plays Top and Right otherwise
3. Right if player 1 plays Top and Left otherwise
4. Right if player 1 plays Top and Right otherwise

On the right is the normal-form representation of this game.

General formulation

In order for a game to be in normal form, we are provided with the following data:

• There is a finite set P of players, which we label {1, 2, ..., m}

• Each player k in P has a finite number of pure strategies

$S_k = \{1, 2, \ldots, n_k\}.$

A pure strategy profile is an association of strategies to players, that is an m-tuple

$\vec{s} = (s_1, s_2, \ldots,s_m)$

such that

$s_1 \in S_1, s_2 \in S_2, \ldots, s_m \in S_m$

A payoff function is a function

$F: S_1 \times S_2 \times \ldots \times S_m \rightarrow \mathbb{R}.$

whose intended interpretation is the award given to a single player at the outcome of the game. Accordingly, to completely specify a game, the payoff function has to be specified for each player in the player set P= {1, 2, ..., m}.

Definition: A game in normal form is a structure

$G=\langle P, \mathbf{S}, \mathbf{F}\rangle$

where:

$P=\{1,2, \ldots , m\}$

is a set of players,

$\mathbf{S}= \{S_1, S_2, \ldots, S_m\}$

is an m-tuple of pure strategy sets, one for each player, and

$\mathbf{F} = \{F_1, F_2, \ldots, F_m\}$

is an m-tuple of payoff functions.

References

• D. Fudenberg and J. Tirole, Game Theory, MIT Press, 1991.

• Leyton-Brown, Kevin; Shoham, Yoav (2008), Essentials of Game Theory: A Concise, Multidisciplinary Introduction, San Rafael, CA: Morgan & Claypool Publishers, ISBN 978-1-598-29593-1, http://www.gtessentials.org . An 88-page mathematical introduction; free online at many universities.

• R. D. Luce and H. Raiffa, Games and Decisions, Dover Publications, 1989.

• Shoham, Yoav; Leyton-Brown, Kevin (2009), Multiagent Systems: Algorithmic, Game-Theoretic, and Logical Foundations, New York: Cambridge University Press, ISBN 978-0-521-89943-7, http://www.masfoundations.org . A comprehensive reference from a computational perspective; see Chapter 3. Downloadable free online.

• J. Weibull, Evolutionary Game Theory, MIT Press, 1996

• J. von Neumann and O. Morgenstern, Theory of games and Economic Behavior, John Wiley Science Editions, 1964. This book was initially published by Princeton University Press in 1944.

External links

• http://www.whalens.org/Sofia/choice/matrix.htm