Normal mode

For other types of mode, see Mode (disambiguation).

Vibration of a single normal mode of a circular disc with a pinned boundary condition along the entire outer edge. See other modes.

A normal mode of an oscillating system is a pattern of motion in which all parts of the system move sinusoidally with the same frequency and with a fixed phase relation. The frequencies of the normal modes of a system are known as its natural frequencies or resonant frequencies. A physical object, such as a building, bridge or molecule, has a set of normal modes that depend on its structure, materials and boundary conditions.

When relating to music, normal modes of vibrating instruments (strings, air pipes, drums, etc.) are called "harmonics" or "overtones".

The most general motion of a system is a superposition of its normal modes. The modes are normal in the sense that they can move independently, that is to say that an excitation of one mode will never cause motion of a different mode.

The concept of normal modes also finds application in wave theory, optics, quantum mechanics, and molecular dynamics.

Mode numbers

A mode of vibration is characterized by a modal frequency and a mode shape, and is numbered according to the number of half waves in the vibration. For example, if a vibrating beam with both ends pinned displayed a mode shape of half of a sine wave (one peak on the vibrating beam) it would be vibrating in mode 1. If it had a full sine wave (one peak and one valley) it would be vibrating in mode 2.

In a system with two or more dimensions, such as the pictured disk, each dimension is given a mode number. Using polar coordinates, we have a radial coordinate and an angular coordinate. If you measured from the center outward along the radial coordinate you would encounter a full wave, so the mode number in the radial direction is 2. The other direction is trickier, because only half of the disk is considered due to the antisymmetric (also called skew-symmetry) nature of a disk's vibration in the angular direction. Thus, measuring 180° along the angular direction you would encounter a half wave, so the mode number in the angular direction is 1. So the mode number of the system is 2-1 or 1-2, depending on which coordinate is considered the "first" and which is considered the "second" coordinate (so it is important to always indicate which mode number matches with each coordinate direction).

Each mode is entirely independent of all other modes. Thus all modes have different frequencies (with lower modes having lower frequencies) and different mode shapes.

Nodes

A mode shape of a drum membrane, with nodal lines shown in pale green.

In a one dimensional system at a given mode the vibration will have nodes, or places where the displacement is always zero. These nodes correspond to points in the mode shape where the mode shape is zero. Since the vibration of a system is given by the mode shape multiplied by a time function, the displacement of the node points remain zero at all times.

When expanded to a two dimensional system, these nodes become lines where the displacement is always zero. If you watch the animation above you will see two circles (one about half way between the edge and center, and the other on the edge itself) and a straight line bisecting the disk, where the displacement is close to zero. In a real system these lines would equal zero exactly, as shown to the right.

Coupled oscillators

Consider two equal bodies (not affected by gravity), each of mass, m, attached to three springs, each with spring constant, k. They are attached in the following manner:

where the edge points are fixed and cannot move. We'll use x₁(t) to denote the horizontal displacement of the left mass, and x₂(t) to denote the displacement of the right mass.

If we denote acceleration (the second derivative of x(t) with respect to time) as $\scriptstyle \ddot x$, the equations of motion are:

$m \ddot x_1 = - k x_1 + k (x_2 - x_1) \,\!$

$m \ddot x_2 = - k x_2 + k (x_1 - x_2) \,\!$

Since we expect oscillatory motion, we try:

$x_1(t) = A_1 e^{i \omega t} \,\!$

$x_2(t) = A_2 e^{i \omega t} \,\!$

Substituting these into the equations of motion gives us:

$-\omega^2 m A_1 e^{i \omega t} = - 2 k A_1 e^{i \omega t} + k A_2 e^{i \omega t} \,\!$

$-\omega^2 m A_2 e^{i \omega t} = k A_1 e^{i \omega t} - 2 k A_2 e^{i \omega t} \,\!$

Since the exponential factor is common to all terms, we omit it and simplify:

$(\omega^2 m - 2 k) A_1 + k A_2 = 0 \,\!$

$k A_1 + (\omega^2 m - 2 k) A_2 = 0 \,\!$

And in matrix representation:

$\begin{bmatrix} \omega^2 m - 2 k & k \\ k & \omega^2 m - 2 k \end{bmatrix} \begin{pmatrix} A_1 \\ A_2 \end{pmatrix} = 0$

For this equation to have a non-trivial solution, the matrix on the left must be singular, therefore the determinant of the matrix must be equal to 0, so:

$(\omega^2 m - 2 k)^2 - k^2 = 0 \,\!$

Solving for ω, we have two solutions:

$\omega_1 = \sqrt{\frac{k}{m}},$

$\omega_2 = \sqrt{\frac{3 k}{m}}.$

If we substitute ω₁ into the matrix and solve for (A₁, A₂), we get (1, 1). If we substitute ω₂, we get (1, −1). (These vectors are eigenvectors, and the frequencies are eigenvalues.)

The first normal mode is:

$\vec \eta_1 = \begin{pmatrix} x^1_1(t) \\ x^1_2(t) \end{pmatrix} = c_1 \begin{pmatrix} 1 \\ 1 \end{pmatrix} \cos{(\omega_1 t + \varphi_1)}$

Which corresponds to both masses moving in the same direction at the same time.

The second normal mode is:

$\vec \eta_2 = \begin{pmatrix} x^2_1(t) \\ x^2_2(t) \end{pmatrix} = c_2 \begin{pmatrix} 1 \\ -1 \end{pmatrix} \cos{(\omega_2 t + \varphi_2)}$

This corresponds to the masses moving in the opposite directions, while the center of mass remains stationary.

The general solution is a superposition of the normal modes where c₁, c₂, φ₁, and φ₂, are determined by the initial conditions of the problem.

The process demonstrated here can be generalized and formulated using the formalism of Lagrangian mechanics or Hamiltonian mechanics.

Standing waves

A standing wave is a continuous form of normal mode. In a standing wave, all the space elements (i.e. (x, y, z) coordinates) are oscillating in the same frequency and in phase (reaching the equilibrium point together), but each has a different amplitude.

The general form of a standing wave is:

Ψ(t) = f(x,y,z)(Acos(ωt) + Bsin(ωt))

where ƒ(x, y, z) represents the dependence of amplitude on location and the cosine\sine are the oscillations in time.

Physically, standing waves are formed by the interference (superposition) of waves and their reflections (although one may also say the opposite; that a moving wave is a superposition of standing waves). The geometric shape of the medium determines what would be the interference pattern, thus determines the ƒ(x, y, z) form of the standing wave. This space-dependence is called a normal mode.

Usually, for problems with continuous dependence on (x, y, z) there is no single or finite number of normal modes, but there are infinitely many normal modes. If the problem is bounded (i.e it is defined on a finite section of space) there are countably many (a discrete infinity of ) normal modes (usually numbered n = 1, 2, 3, ...). If the problem is not bounded, there is a continuous spectrum of normal modes.

Elastic solids

See: Einstein solid and Debye model

In any solid at any temperature, the primary particles (e.g. atoms or molecules) are not stationary, but rather vibrate about mean positions. In insulators the capacity of the solid to store thermal energy is due almost entirely to these vibrations. Many physical properties of the solid (e.g. modulus of elasticity) can be predicted given knowledge of the frequencies with which the particles vibrate. The simplest assumption (by Einstein) is that all the particles oscillate about their mean positions with the same natural frequency ν. This is equivalent to the assumption that all atoms vibrate independently with a frequency ν. Einstein also assumed that the allowed energy states of these oscillations are harmonics, or integral multiples of hν. The spectrum of waveforms can be described mathematically using a Fourier series of sinusoidal density fluctuations (or thermal phonons).

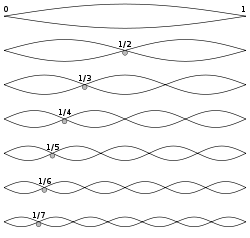The fundamental and the first six overtones of a vibrating string. The mathematics of wave propagation in crystalline solids consists of treating the harmonics as an ideal Fourier series of sinusoidal density fluctuations (or atomic displacement waves).

Debye subsequently recognized that each oscillator is intimately coupled to its neighboring oscillators at all times. Thus, by replacing Einstein's identical uncoupled oscillators with the same number of coupled oscillators, Debye correlated the elastic vibrations of a one-dimensional solid with the number of mathematically special modes of vibration of a stretched string (see figure). The pure tone of lowest pitch or frequency is referred to as the fundamental and the multiples of that frequency are called its harmonic overtones. He assigned to one of the oscillators the frequency of the fundamental vibration of the whole block of solid. He assigned to the remaining oscillators the frequencies of the harmonics of that fundamental, with the highest of all these frequencies being limited by the motion of the smallest primary unit.

The normal modes of vibration of a crystal are in general superpositions of many overtones, each with an appropriate amplitude and phase. Longer wavelength (low frequency) phonons are exactly those acoustical vibrations which are considered in the theory of sound. Both longitudinal and transverse waves can be propagated through a solid, while, in general, only longitudinal waves are supported by fluids.

In the longitudinal mode, the displacement of particles from their positions of equilibrium coincides with the propagation direction of the wave. Mechanical longitudinal waves have been also referred to as compression waves. For transverse modes, individual particles move perpendicular to the propagation of the wave.

According to quantum theory, the mean energy of a normal vibrational mode of a crystalline solid with characteristic frequency υ is:

$E(v)=\frac{1}{2}hv+\frac{hv}{e^{hv/kT}-1}$

The term (1/2)hυ represents the "zero-point energy", or the energy which an oscillator will have at absolute zero. E (ν ) tends to the classic value kT at high temperatures

$E(v)=kT\left[1+\frac{1}{12}\frac{hv^2}{kT}+O\left(\frac{hv}{kT}\right)^4+\cdots\right]$

The entropy per normal mode is:

$\begin{align} S\left(v\right)&=\int_0^T\frac{d}{dT}E\left(v\right)\frac{dT}{T}\\[10pt] &=\frac{E\left(v\right)}{T}-k\log\left(1-e^{-\frac{hv}{kT}}\right) \end{align}$

The free energy is:

$F(v)=E-TS=kT\log \left(1-e^{-\frac{hv}{kT}}\right)$

which, for kT >> hν, tends to:

$F(v)=kT\log \left(\frac{hv}{kT}\right)$

In order to calculate the internal energy and the specific heat, we must know the number of normal vibrational modes a frequency between the values ν and ν + dν. Allow this number to be f (ν)dν. Since the total number of normal modes is 3N, the function f (ν) is given by:

$\int f(v)\,dv=3N$

The integration is performed over all frequencies of the crystal. Then the internal energy U will be given by:

$U=\int f(v)E(v)\,dv$

Quantum mechanics

In quantum mechanics, a state $\ | \psi \rang$ of a system is described by a wavefunction $\ \psi (x, t)$ which solves the Schrödinger equation. The square of the absolute value of $\ \psi$ ,i.e.

$\ P(x,t) = |\psi (x,t)|^2$

is the probability density to measure the particle in place x at time t.

Usually, when involving some sort of potential, the wavefunction is decomposed into a superposition of energy eigenstates, each oscillating with frequency of $\omega = E_n / \hbar$. Thus, we may write

$|\psi (t) \rang = \sum_n |n\rang \left\langle n | \psi ( t=0) \right\rangle e^{-iE_nt/\hbar}$

The eigenstates have a physical meaning further than an orthonormal basis. When the energy of the system is measured, the wavefunction collapses into one of its eigenstates and so the particle wavefunction is described by the pure eigenstate corresponding to the measured energy.

Earth

Normal modes are generated in the earth from long wavelength seismic waves from large earthquakes interfering to form standing waves.

For an elastic, isotropic, homogeneous sphere, spheroidal, toroidal and radial (or breathing modes) arise. Spheroidal modes only involve P and SV waves (like Rayleigh waves) and depend on overtone number n and angular order l but have degeneracy of azimuthal order m. Increasing l concentrates fundamental branch closer to surface and at large l this tends to Rayleigh waves. Toroidal modes only involve SH waves (like Love waves) and do not exist in fluid outer core. Radial modes are just a subset of spheroidal modes with l=0. The degeneracy doesn’t exists on Earth as it is broken by rotation, ellipticity and 3D heterogeneous velocity and density structure.

We either assume that each mode can be isolated, the self-coupling approximation, or that many modes close in frequency resonant, the cross-coupling approximation. Self-coupling will change just the phase velocity and not the number of waves around a great circle resulting in a stretching or shrinking of standing wave pattern. Cross-coupling can be caused by rotation of Earth leading to mixing of fundamental spheroidal and toroidal modes, or by aspherical mantle structure or Earth’s ellipticity.

See also

• Specific types:
  • Longitudinal mode
  • Transverse mode
  • Torsional vibration
• Physical applications:
  • Waves
  • Optics
  • Harmonic oscillator
  • Vibrational spectroscopy
  • Mechanical resonance
  • Critical speed
  • Quantum theory
    • Schrödinger equation
    • Wavefunction
    • Measurement in quantum mechanics
    • Quantum vibration
  • Harmonic series (music)
  • Leaky mode
  • Seismology
  • Cymatics
  • Earthquake engineering
  • Modal Analysis
  • Room acoustics
  • Vibrations of a circular drum
• Mathematical tools:
  • Linear algebra
  • Eigenvectors
  • Differential equations
  • Fourier analysis
  • Sturm–Liouville theory
  • Boundary value problem
  • Wave equation
  • Chladni patterns

References

• Blevins, Robert D.. Formulas for natural frequency and mode shape. 
• Tzou, H. S.; Bergman, L. A.. Dynamics and Control of Distributed Systems. 
• Deuss, Arwen (2010-2011). Physics of the Earth as a Planet Lecture Notes. Cambridge University. 

External links

• Java simulation of coupled oscillators.
• Java simulation of the normal modes of a string, drum, and bar.
• Photograph of a cup of coffee vibrating at a normal mode frequency
• Mode shape visualization of real structures