- Cyclic order
-

In mathematics, a cyclic order is a way to arrange a set of objects in a circle.[nb] Unlike most structures in order theory, a cyclic order cannot be modeled as a binary relation "a < b". One does not say that east is more clockwise than west. Instead, a cyclic order is defined as a ternary relation [a, b, c], meaning "after a, one reaches b before c". For example, [June, October, February]. A ternary relation is called a cyclic order if it is cyclic, asymmetric, transitive, and total. Dropping the "total" requirement results in a partial cyclic order.
A set with a cyclic order is called a cyclically ordered set or simply a cycle.[nb] Some familiar cycles are discrete, having only a finite number of elements: there are seven days of the week, four cardinal directions, twelve notes in the chromatic scale, and three plays in rock-paper-scissors. In a finite cycle, each element has a "next element" and a "previous element". There are also continuously variable cycles with infinitely many elements, such as the oriented unit circle in the plane.
Cyclic orders are closely related to linear orders, which arrange objects in a line. Any linear order can be bent into a circle, and any cyclic order can be cut at a point, resulting in a line. These operations, along with the related constructions of intervals and covering maps, mean that questions about cyclic orders can often be transformed into questions about linear orders, which are more familiar. Cycles have more symmetries than linear orders, so they are often more compatible with other mathematical structures. The integers form a linearly ordered group Z, whose quotient by a number n, the finite cyclic group Z/n, is circularly orderable but not linearly orderable. The real numbers form a linearly ordered topological space R, whose one-point compactification, the real projective line RP1, is circularly orderable but not linearly orderable.
Contents
Finite cycles
In other words, a finite cycle is the same as a cycle of a permutation.
A cyclic order on a set X with n elements is an arrangement of X as on a clock face, for an n-hour clock. That is, rather than an order relation on X, we define on X just functions 'element immediately before' and 'element immediately following' any given x, in such a way that taking predecessors, or successors, cycles once through the elements as x(1), x(2), ..., x(n). Another way to put it is to say that we make X into the standard directed cycle graph on n vertices, by some matching of elements to vertices.
It can be instinctive to use cyclic orders for symmetric functions, for example as in
- xy + yz + zx
where writing the final monomial as xz would distract from the pattern.
A substantial use of cyclic orders is in the determination of the conjugacy classes of free groups. Two elements g and h of the free group F on a set Y are conjugate if and only if, when they are written as products of elements y and y−1 with y in Y, and then those products are put in cyclic order, the cyclic orders are equivalent under the rewriting rules that allow one to remove or add adjacent y and y−1.
A cyclic order on a set X can be determined by a linear order on X, but not in a unique way. Choosing a linear order is equivalent to choosing a first element, so there are exactly n linear orders that induce a given cyclic order. Since there are n! possible linear orders, there are n! / n = (n − 1)! possible cyclic orders.
Definitions
An infinite set can also be ordered cyclically. Important examples of infinite cycles include the unit circle, S1, and the rational numbers, Q. The basic idea is the same: we arrange elements of the set around a circle. However, in the infinite case we cannot use the immediate successor relation; instead we use a ternary relation denoting that elements a, b, c occur after each other (not necessarily immediately) as we go around the circle.
By currying the arguments of the ternary relation [a, b, c], one can think of a cyclic order as a one-parameter family of binary order relations, called cuts, or as a two-parameter family of subsets of K, called intervals.
The ternary relation
The general definition is as follows: a cyclic order on a set X is a relation C ⊂ X3, written [a, b, c], that satisfies the following axioms:[nb]
- Cyclicity: If [a, b, c] then [b, c, a]
- Asymmetry: If [a, b, c] then not [c, b, a]
- Transitivity: If [a, b, c] and [a, c, d] then [a, b, d]
- Totality: If a, b, and c are distinct, then either [a, b, c] or [c, b, a]
The axioms are named by analogy with the asymmetry, transitivity, and totality axioms for a binary relation, which together define a strict linear order. Edward Huntington (1916, 1924) considered other possible lists of axioms, including one list meant to emphasize the similarity between a cyclic order and a betweenness relation. A ternary relation that satisfies the first three axioms, but not necessarily the axiom of totality, is a partial cyclic order.
Rolling and cuts
Given a linear order < on a set X, the cyclic order on X induced by < is defined as follows:[2]
- [a, b, c] if and only if a < b < c or b < c < a or c < a < b
Two linear orders induce the same cyclic order if they can be transformed into each other by a cyclic rearrangement, as in cutting a deck of cards.[3] One may define a cyclic order relation as a ternary relation that is induced by a strict linear order as above.[4]
Cutting a single point out of a cyclic order leaves a linear order behind. More precisely, given a cyclically ordered set (K, [ ]), each element a ∈ K defines a natural linear order <a on the remainer of the set, K ∖ a, by the following rule:[5]
- x <a y if and only if [a, x, y].
Moreover, <a can be extended by adjoining a as a least element; the resulting linear order on K is called the principal cut with least element a. Likewise, adjoining a as a greatest element results in a cut <a.[6]
Intervals
Given two elements a ≠ b ∈ K, the open interval from a to b, written (a, b), is the set of all x ∈ K such that [a, x, b]. The system of open intervals completely defines the cyclic order and can be used as an alternate definition of a cyclic order relation.[7]
An interval (a, b) has a natural linear order given by <a. One can define half-closed and closed intervals [a, b), (a, b], and [a, b] by adjoining a as a least element and/or b as a greatest element.[8] As a special case, the open interval (a, a) is defined as the cut K ∖ a.
More generally, a proper subset S of K is called convex if it contains an interval between every pair of points: for a ≠ b ∈ S, either (a, b) or (b, a) must also be in S.[9] A convex set is linearly ordered by the cut <x for any x not in the set; this ordering is independent of the choice of x.
Monotone functions
The "cyclic order = arranging in a circle" idea works because any subset of a cycle is itself a cycle. In order to use this idea to impose cyclic orders on sets that are not actually subsets of the unit circle in the plane, it is necessary to consider functions between sets.
A function between two cyclically ordered sets, f : X → Y, is called a monotonic function or a homomorphism if it pulls back the ordering on Y: whenever [f(a), f(b), f(c)], one has [a, b, c]. Equivalently, f is monotone if whenever [a, b, c] and f(a), f(b), and f(c) are all distinct, then [f(a), f(b), f(c)]. A typical example of a monotone function is the following function on the cycle with 6 elements:
- f(0) = f(1) = 4,
- f(2) = f(3) = 0,
- f(4) = f(5) = 1.
A function is called an embedding if it is both monotone and injective.[nb] Equivalently, an embedding is a function that pushes forward the ordering on X: whenever [a, b, c], one has [f(a), f(b), f(c)]. As an important example, if X is a subset of a cyclically ordered set Y, and X is given its natural ordering, then the inclusion map i : X → Y is an embedding.
Generally, an injective function f from an unordered set X to a cycle Y induces a unique cyclic order on X that makes f an embedding.
Functions on finite sets
A cyclic order on a finite set X can be determined by an injection into the unit circle, X → S1. There are many possible functions that induce the same cyclic order—in fact, infinitely many. In order to quantify this redundancy, it takes a more complex combinatorial object than a simple number. Examining the configuration space of all such maps leads to the definition of an (n − 1)-dimensional polytope known as a cyclohedron. Cyclohedra were first applied to the study of knot invariants;[10] they have more recently been applied to the experimental detection of periodically expressed genes in the study of biological clocks.[11]
The category of homomorphisms of the standard finite cycles is called the cyclic category; it may be used to consrtuct Alain Connes' cyclic homology.
One may define a degree of a function between cycles, analogous to the degree of a continuous mapping. For example, the natural map from the circle of fifths to the chromatic circle is a map of degree 7. One may also define a rotation number.
Completion
- A cut with both a least element and a greatest element is called a jump. For example, every cut of a finite cycle Zn is a jump. A cycle with no jumps is called dense.[12][13]
- A cut with neither a least element nor a greatest element is called a gap. For example, the rational numbers Q have a gap at every irrational number. They also have a gap at infinity, i.e. the usual ordering. A cycle with no gaps is called complete.[14][13]
- A cut with exactly one endpoint is called a principal or Dedekind cut. For example, every cut of the circle S1 is a principal cut. A cycle where every cut is principal, being both dense and complete, is called continuous.[15][13]
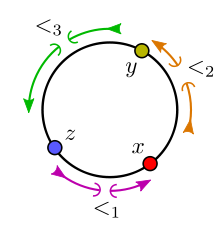
The set of all cuts is cyclically ordered by the following relation: [<1, <2, <3] if and only if there exist x, y, z such that:[16]
- x <1 y <1 z,
- x <1 y <2 z <2 x, and
- x <1 y <1 z <3 x <3 y.
A certain subset of this cycle of cuts is the Dedekind completion of the original cycle.
Further constructions
Unrolling and covers
Starting from a cyclically ordered set K, one may form a linear order by unrolling it along an infinite line. This captures the intuitive notion of keeping track of how many times one goes around the circle. Formally, one defines a linear order on the Cartesian product Z × K, where Z is the set of integers, by fixing an element a and requiring that for all i:[17]
- If [a, x, y], then ai < xi < yi < ai + 1.
For example, the months January 2011, May 2011, September 2011, and January 2012 occur in that order.
This ordering of Z × K is called the universal cover of K.[nb] Its order type is independent of the choice of a, but the notation is not, since the integer coordinate "rolls over" at a. For example, although the cyclic order of pitch classes is compatible with the A-to-G alphabetical order, C is chosen to be the first note in each octave, so in note-octave notation, B3 is followed by C4.
The inverse construction starts with a linearly ordered set and coils it up into a cyclically ordered set. Given a linearly ordered set L and an order-preserving bijection T : L → L with unbounded orbits, the orbit space L / T is cyclically ordered by the requirement:[7][nb]
- If a < b < c < T(a), then [[a], [b], [c]].
In particular, one can recover K by defining T(xi) = xi + 1 on Z × K.
There are also n-fold coverings for finite n; in this case, one cyclically ordered set covers another cyclically ordered set. For example, the 24-hour clock is a double cover of the 12-hour clock. In geometry, the pencil of rays emanating from a point in the oriented plane is a double cover of the pencil of unoriented lines passing through the same point.[18] These covering maps can be characterized by lifting them to the universal cover.[7]
Products and retracts
Given a cyclically ordered set (K, [ ]) and a linearly ordered set (L, <), the (total) lexicographic product is a cyclic order on the product set K × L, defined by [(a, x), (b, y), (c, z)] if one of the following holds:[19]
- [a, b, c]
- a = b ≠ c and x < y
- b = c ≠ a and y < z
- c = a ≠ b and z < x
- a = b = c and [x, y, z]
The lexicographic product K × L globally looks like K and locally looks like L; it can be thought of as K copies of L. This construction is sometimes used to characterize cyclically ordered groups.[20]
One can also glue together different linearly ordered sets to form a circularly ordered set. For example, given two linearly ordered sets L1 and L2, one may form a circle by joining them together at positive and negative infinity. A circular order on the disjoint union L1 ∪ L2 ∪ {–∞, ∞} is defined by ∞ < L1 < –∞ < L2 < ∞, where the induced ordering on L1 is the opposite of its original ordering. For example, the set of all longitudes is circularly ordered by joining together all points west and all points east, along with the prime meridian and the 180th meridian. Kuhlmann, Marshall & Osiak (2011) use this construction while characterizing the spaces of orderings and real places of double formal Laurent series over a real closed field.[21]
Topology
The open intervals form a base for a natural topology, the cyclic order topology. The open sets in this topology are exactly those sets which are open in every compatible linear order.[22] To illustrate the difference, in the set [0, 1), the subset [0, 1/2) is a neighborhood of 0 in the linear order but not in the cyclic order.
Interesting examples of cyclically ordered spaces include the conformal boundary of a simply connected Lorentz surface[23] and the leaf space of a lifted essential lamination of certain 3-manifolds.[24] Discrete dynamical systems on cyclically ordered spaces have also been studied.[25]
The interval topology forgets the original orientation of the cyclic order. This orientation can be restored by enriching the intervals with their induced linear orders; then one has a set covered with an atlas of linear orders that are compatible where they overlap. In other words, a cyclically ordered set can be thought of as a locally linearly ordered space: an object like a manifold, but with order relations instead of coordinate charts. This viewpoint makes it easier to be precise about such concepts as covering maps. The generalization to a locally partially ordered space is studied in Roll (1993); see also Directed topology.
Related structures
Groups
Main article: Cyclically ordered groupA cyclically ordered group is a set with both a group structure and a cyclic order, such that left and right multiplication both preserve the cyclic order.
Modified axioms
A partial cyclic order is a ternary relation that generalizes a (total) cyclic order in the same way that a partial order generalizes a total order. It is cyclic, asymmetric, and transitive, but it need not be total. An order variety is a partial cyclic order that satisfies an additional spreading axiom. Replacing the asymmetry axiom with a complementary version results in the definition of a co-cyclic order. Appropriately total co-cyclic orders are related to cyclic orders in the same way that ≤ is related to <.
A cyclic order obeys a relatively strong 4-point transitivity axiom. One structure that weakens this axiom is a CC system: a ternary relation that is cyclic, asymmetric, and total, but generally not transitive. Instead, a CC system must obey a 5-point transitivity axiom and a new interiority axiom, which constrains the 4-point configurations that violate cyclic transitivity.[26]
A cyclic order is required to be symmetric under cyclic permutation, [a, b, c] ⇒ [b, c, a], and asymmetric under reversal: [a, b, c] ⇒ ¬[c, b, a]. A ternary relation that is asymmetric under cyclic permutation and symmetric under reversal, together with appropriate versions of the transitivity and totality axioms, is called a betweenness relation. A separation relation is a quaternary relation that can be thought of as a cyclic order without an orientation. The relationship between a circular order and a separation relation is analogous to the relationship between a linear order and a betweenness relation.[27]
Symmetries and model theory
Evans, Macpherson & Ivanov (1997) provide a model-theoretic description of the covering maps of cycles.
Tararin (2001, 2001) studies groups of automorphisms of cycles with various transitivity properties. Giraudet & Holland (2002) characterize cycles whose full automorphism groups act freely and transitively. Campero-Arena & Truss (2009) characterize countable colored cycles whose automorphism groups act transitively. Truss (2009) studies the automorphism group of the unique (up to isomorphism) countable dense cycle.
Kulpeshov & Macpherson (2005) study minimality conditions on circularly ordered structures, i.e. models of first-order languages that include a cyclic order relation. These conditions are analogues of o-minimality and weak o-minimality for the case of linearly ordered structures. Kulpeshov (2006, 2009) continues with some characterizations of ω-categorical structures.[28]
Cognition
Hans Freudenthal has emphasized the role of cyclic orders in cognitive development, as a contrast to Jean Piaget who addresses only linear orders. Some experiments have been performed to investigate the mental representations of cyclically ordered sets, such as the months of the year.
Notes on usage
^cyclic order The relation may be called a cyclic order (Huntington 1916, p. 630), a circular order (Huntington 1916, p. 630), a cyclic ordering (Kok 1973, p. 6), or a circular ordering (Mosher 1996, p. 109). Some authors call such an ordering a total cyclic order (Isli & Cohn 1998, p. 643), a complete cyclic order (Novák 1982, p. 462), a linear cyclic order (Novák 1984, p. 323), or an l-cyclic order or ℓ-cyclic order (Černák 2001, p. 32), to distinguish from the broader class of partial cyclic orders, which they call simply cyclic orders. Finally, some authors may take cyclic order to mean an unoriented quaternary separation relation (Bowditch 1998, p. 155).
^cycle A set with a cyclic order may be called a cycle (Novák 1982, p. 462) or a circle (Giraudet & Holland 2002, p. 1). The above variations also appear in adjective form: cyclically ordered set (cyklicky uspořádané množiny, Čech 1936, p. 23), circularly ordered set, total cyclically ordered set, complete cyclically ordered set, linearly cyclically ordered set, l-cyclically ordered set, ℓ-cyclically ordered set. All authors agree that a cycle is totally ordered.
^ternary relation There are a few different symbols in use for a cyclic relation. Huntington (1916, p. 630) uses concatenation: ABC. Čech (1936, p. 23) and (Novák 1982, p. 462) use ordered triples and the set membership symbol: (a, b, c) ∈ C. Megiddo (1976, p. 274) uses concatenation and set membership: abc ∈ C, understanding abc as a cyclically ordered triple. The literature on groups, such as Świerczkowski (1959a, p. 162) and Černák & Jakubík (1987, p. 157), tend to use square brackets: [a, b, c]. Giraudet & Holland (2002, p. 1) use round parentheses: (a, b, c), reserving square brackets for a betweenness relation. Campero-Arena & Truss (2009, p. 1) use a function-style notation: R(a, b, c). Rieger (1947, cited after Pecinová 2008, p. 82) uses a "less-than" symbol as a delimiter: < x, y, z <. Some authors use infix notation: a < b < c, with the understanding that this does not carry the usual meaning of a < b and b < c for some binary relation < (Černy 1978, p. 262). Weinstein (1996, p. 81) emphasizes the cyclic nature by repeating an element: p ↪ r ↪ q ↪ p.
^embedding Novák (1984, p. 332) calls an embedding an "isomorphic embedding".
^roll In this case, Giraudet & Holland (2002, p. 2) write that K is L "rolled up".
^orbit space The map T is called archimedean by Bowditch (2004, p. 33), coterminal by Campero-Arena & Truss (2009, p. 582), and a translation by McMullen (2009, p. 10).
^universal cover McMullen (2009, p. 10) calls Z × K the "universal cover" of K. Giraudet & Holland (2002, p. 3) write that K is Z × K "coiled". Freudenthal & Bauer (1974, p. 10) call Z × K the "∞-times covering" of K. Often this construction is written as the anti-lexicographic order on K × Z.
References
- Citations
- ^ Brown 1987, p. 52.
- ^ Huntington 1935, p. 6; Čech 1936, p. 25.
- ^ Calegari 2004, p. 439.
- ^ Courcelle 2003.
- ^ Huntington 1935, p. 7; Čech 1936, p. 24.
- ^ Novák 1984, p. 323.
- ^ a b c McMullen 2009, p. 10.
- ^ Giraudet & Holland 2002, p. 2.
- ^ Kulpeshov 2009.
- ^ Stasheff 1997, p. 58.
- ^ Morton et al. 2007.
- ^ Novák 1984, p. 325.
- ^ a b c Novák & Novotný 1987, p. 409–410.
- ^ Novák 1984, pp. 325, 331.
- ^ Novák 1984, p. 333.
- ^ Novák 1984, p. 330.
- ^ Roll 1993, p. 469; Freudenthal & Bauer 1974, p. 10
- ^ Freudenthal 1973, p. 475; Freudenthal & Bauer 1974, p. 10
- ^ Świerczkowski 1959a, p. 161.
- ^ Świerczkowski 1959a.
- ^ Kuhlmann, Marshall & Osiak 2011, p. 8.
- ^ Viro et al. 2008, p. 44.
- ^ Weinstein 1996, pp. 80–81.
- ^ Calegari & Dunfield 2003, pp. 12–13.
- ^ Bass et al. 1996, p. 19.
- ^ Knuth 1992, p. 4.
- ^ Huntington 1935.
- ^ Macpherson 2011.
- Bibliography
- Bass, Hyman; Otero-Espinar, Maria Victoria; Rockmore, Daniel; Tresser, Charles (1996), Cyclic renormallzatlon and automorphism groups of rooted trees, Lecture Notes in Mathematics, 1621, Springer, doi:10.1007/BFb0096321, ISBN 978-3-540-60595-9
- Bowditch, Brian H. (September 1998), "Cut points and canonical splittings of hyperbolic groups", Acta Mathematica 180 (2): 145–186, doi:10.1007/BF02392898, http://www.kryakin.com/files/Acta_Mat_(2_55)/acta197_151/180/180_1.pdf, retrieved 25 April 2011
- Bowditch, Brian H. (November 2004), "Planar groups and the Seifert conjecture", Journal für die reine und angewandte Mathematik 576: 11–62, doi:10.1515/crll.2004.084, http://www.warwick.ac.uk/~masgak/abstracts/pla.html, retrieved 31 May 2011
- Brown, Kenneth S. (February 1987), "Finiteness properties of groups", Journal of Pure and Applied Algebra 44 (1–3): 45–75, doi:10.1016/0022-4049(87)90015-6, http://www.math.cornell.edu/~kbrown/scan/1987.0044.0045.pdf, retrieved 21 May 2011
- Calegari, Danny (13 December 2004), "Circular groups, planar groups, and the Euler class", Geometry & Topology Monographs 7: 431–491, arXiv:math/0403311, doi:10.2140/gtm.2004.7.431, http://emis.math.ca/journals/UW/gt/ftp/main/m7/m7-15.pdf, retrieved 30 April 2011
- Calegari, Danny; Dunfield, Nathan M. (April 2003), "Laminations and groups of homeomorphisms of the circle", Inventiones mathematicae 152 (1): 149–204, arXiv:math/0203192, doi:10.1007/s00222-002-0271-6
- Campero-Arena, G.; Truss, John K. (April 2009), "1-transitive cyclic orderings", Journal of Combinatorial Theory, Series A 116 (3): 581–594, doi:10.1016/j.jcta.2008.08.006, http://www.maths.leeds.ac.uk/pure/staff/truss/g.pdf, retrieved 25 April 2011
- Čech, Eduard (1936) (in Czech), Bodové množiny, Prague: Jednota Československých matematiků a fysiků, doi:10338.dmlcz/400435, http://dml.cz/handle/10338.dmlcz/400435, retrieved 9 May 2011
- Černák, Štefan (2001), "Cantor extension of a half linearly cyclically ordered group", Discussiones Mathematicae - General Algebra and Applications 21 (1): 31–46, http://lord.uz.zgora.pl:7777/bib/bibwww.pdf?nIdA=4493, retrieved 22 May 2011
- Černák, Štefan; Jakubík, Ján (1987), "Completion of a cyclically ordered group", Czechoslovak Mathematical Journal 37 (1): 157–174, MR875137, Zbl 0624.06021, hdl:10338.dmlcz/102144, http://dspace.dml.cz/bitstream/handle/10338.dmlcz/102144/CzechMathJ_37-1987-1_16.pdf, retrieved 25 April 2011
- Černy, Ilja (1978), "Cuts in simple connected regions and the cyclic ordering of the system of all boundary elements", Časopis pro pěstování matematiky 103 (3): 259–281, doi:10338.dmlcz/117983, http://dml.cz/bitstream/handle/10338.dmlcz/117983/CasPestMat_103-1978-3_6.pdf, retrieved 11 May 2011
- Courcelle, Bruno (21 August 2003), "2.3 Circular order", in Berwanger, Dietmar; Grädel, Erich, Problems in Finite Model Theory, p. 12, http://www-mgi.informatik.rwth-aachen.de/FMT/problems.pdf, retrieved 15 May 2011
- Evans, David M.; Macpherson, Dugald; Ivanov, Alexandre A. (1997), "Finite Covers", in Evans, David M., Model theory of groups and automorphism groups: Blaubeuren, August 1995, London Mathematical Society Lecture Note Series, 244, Cambridge University Press, pp. 1–72, ISBN 0-521-58955-X, http://www.amsta.leeds.ac.uk/Pure/preprints/hdm/hdm5.ps, retrieved 5 May 2011
- Freudenthal, Hans (1973), Mathematics as an educational task, D. Reidel, ISBN 90-277-0235-7
- Freudenthal, Hans; Bauer, A. (1974), "Geometry—A Phenomenological Discussion", in Behnke, Heinrich; Gould, S. H., Fundamentals of mathematics, 2, MIT Press, pp. 3–28, ISBN 0-262-02069-6
- Freudenthal, Hans (1983), Didactical phenomenology of mathematical structures, D. Reidel, ISBN 90-277-1535-1
- Giraudet, Michèle; Holland, W. Charles (September 2002), "Ohkuma Structures", Order 19 (3): 223–237, doi:10.1023/A:1021249901409, http://web.mac.com/chollan1/iWeb/Site/publications_files/55%20Ohkuma%20structures.pdf, retrieved 28 April 2011
- Huntington, Edward V. (1 November 1916), "A Set of Independent Postulates for Cyclic Order", Proceedings of the National Academy of Sciences of the United States of America 2 (11): 630–631, http://www.pnas.org/content/2/11/630.full.pdf, retrieved 8 May 2011
- Huntington, Edward V. (15 February 1924), "Sets of Completely Independent Postulates for Cyclic Order", Proceedings of the National Academy of Sciences of the United States of America 10 (2): 74–78, http://www.pnas.org/content/10/2/74.full.pdf, retrieved 8 May 2011
- Huntington, Edward V. (July 1935), "Inter-Relations Among the Four Principal Types of Order", Transactions of the American Mathematical Society 38 (1): 1–9, doi:10.1090/S0002-9947-1935-1501800-1, http://www.ams.org/journals/tran/1935-038-01/S0002-9947-1935-1501800-1/S0002-9947-1935-1501800-1.pdf, retrieved 8 May 2011
- Isli, Amar; Cohn, Anthony G. (1998), "An algebra for cyclic ordering of 2D orientations", AAAI '98/IAAI '98 Proceedings of the fifteenth national/tenth conference on Artificial intelligence/Innovative applications of artificial intelligence, ISBN 0-262-51098-7, https://www.aaai.org/Papers/AAAI/1998/AAAI98-091.pdf, retrieved 23 May 2011
- Knuth, Donald E. (1992), Axioms and Hulls, Lecture Notes in Computer Science, 606, Heidelberg: Springer-Verlag, pp. ix+109, doi:10.1007/3-540-55611-7, ISBN 3-540-55611-7, http://www-cs-faculty.stanford.edu/~uno/aah.html, retrieved 5 May 2011
- Kok, H. (1973), Connected orderable spaces, Amsterdam: Mathematisch Centrum, ISBN 9061960886
- Kuhlmann, Salma; Marshall, Murray; Osiak, Katarzyna (1 June 2011), "Cyclic 2-structures and spaces of orderings of power series fields in two variables", Journal of Algebra 335 (1): 36–48, doi:10.1016/j.jalgebra.2011.02.026, http://math.usask.ca/~marshall/r%5B%5Bx,y%5D%5D_20,11.pdf, retrieved 11 May 2011
- Kulpeshov, Beibut Sh. (December 2006), "On ℵ0-categorical weakly circularly minimal structures", Mathematical Logic Quarterly 52 (6): 555–574, doi:10.1002/malq.200610014
- Kulpeshov, Beibut Sh. (March 2009), "Definable functions in the ℵ0-categorical weakly circularly minimal structures", Siberian Mathematical Journal 50 (2): 282–301, doi:10.1007/s11202-009-0034-3 Translation of Kulpeshov (2009), "Определимые функции в ℵ0-категоричных слабо циклически минимальных структурах", Sibirskiĭ Matematicheskiĭ Zhurnal 50 (2): 356–379, http://mi.mathnet.ru/eng/smj1965, retrieved 24 May 2011
- Kulpeshov, Beibut Sh.; Macpherson, H. Dugald (July 2005), "Minimality conditions on circularly ordered structures", Mathematical Logic Quarterly 51 (4): 377–399, doi:10.1002/malq.200410040, MR2150368
- Macpherson, H. Dugald (2011), "A survey of homogeneous structures", Discrete Mathematics, doi:10.1016/j.disc.2011.01.024, http://www.amsta.leeds.ac.uk/pure/staff/macpherson/homog_final2.pdf, retrieved 28 April 2011
- McMullen, Curtis T. (2009), "Ribbon R-trees and holomorphic dynamics on the unit disk", Journal of Topology 2 (1): 23–76, doi:10.1112/jtopol/jtn032, http://www.math.harvard.edu/~ctm/papers/home/text/papers/rtrees/rtrees.pdf, retrieved 15 May 2011
- Megiddo, Nimrod (March 1976), "Partial and complete cyclic orders", Bulletin of the American Mathematical Society 82 (2): 274–276, doi:10.1090/S0002-9904-1976-14020-7, http://www.ams.org/journals/bull/1976-82-02/S0002-9904-1976-14020-7/S0002-9904-1976-14020-7.pdf, retrieved 30 April 2011
- Morton, James; Pachter, Lior; Shiu, Anne; Sturmfels, Bernd (January 2007), "The Cyclohedron Test for Finding Periodic Genes in Time Course Expression Studies", Statistical Applications in Genetics and Molecular Biology 6 (1), arXiv:q-bio/0702049, doi:10.2202/1544-6115.1286
- Mosher, Lee (1996), "A user's guide to the mapping class group: once-punctured surfaces", in Baumslag, Gilbert, Geometric and computational perspectives on infinite groups, DIMACS, 25, AMS Bookstore, pp. 101–174, arXiv:math/9409209, ISBN 0-8218-0449-9
- Novák, Vítězslav (1982), "Cyclically ordered sets", Czechoslovak Mathematical Journal 32 (3): 460–473, doi:10338.dmlcz/101821, http://dml.cz/bitstream/handle/10338.dmlcz/101821/CzechMathJ_32-1982-3_12.pdf, retrieved 30 April 2011
- Novák, Vítězslav (1984), "Cuts in cyclically ordered sets", Czechoslovak Mathematical Journal 34 (2): 322–333, doi:10338.dmlcz/101955, http://dml.cz/bitstream/handle/10338.dmlcz/101955/CzechMathJ_34-1984-2_17.pdf, retrieved 30 April 2011
- Novák, Vítězslav; Novotný, Miroslav (1987), "On completion of cyclically ordered sets", Czechoslovak Mathematical Journal 27 (3): 407–414, doi:10338.dmlcz/102168, http://dspace.dml.cz/bitstream/handle/10338.dmlcz/102168/CzechMathJ_37-1987-3_6.pdf, retrieved 25 April 2011
- Pecinová, Eliška (2008) (in Czech), Ladislav Svante Rieger (1916–1963), Dějiny matematiky, 36, Prague: Matfyzpress, doi:10338.dmlcz/400757, ISBN 978-80-7378-047-0, http://dml.cz/handle/10338.dmlcz/400757, retrieved 9 May 2011
- Rieger, L. S. (1947), "О uspořádaných a cyklicky uspořádaných grupách II (On ordered and cyclically ordered groups II)" (in Czech), Věstník Královské české spolecnosti nauk, Třída mathematicko-přírodovědná (Journal of the Royal Czech Society of Sciences, Mathematics and natural history) (1): 1–33
- Roll, J. Blair (1993), "Locally partially ordered groups", Czechoslovak Mathematical Journal 43 (3): 467–481, hdl:10338.dmlcz/128411, http://dml.cz/bitstream/handle/10338.dmlcz/128411/CzechMathJ_43-1993-3_8.pdf, retrieved 30 April 2011
- Stasheff, Jim (1997), "From operads to 'physically' inspired theories", in Loday, Jean-Louis; Stasheff, James D.; Voronov, Alexander A., Operads: Proceedings of Reneassance Conferences, Contemporary Mathematics, 202, AMS Bookstore, pp. 53–82, ISBN 978-0-8218-0513-8, http://www.math.unc.edu/Faculty/jds/operadchik.ps, retrieved 1 May 2011
- Świerczkowski, S. (1959a), "On cyclically ordered groups", Fundamenta Mathematicae 47: 161–166, http://matwbn.icm.edu.pl/ksiazki/fm/fm47/fm4718.pdf, retrieved 2 May 2011
- Tararin, Valeri Mikhailovich (2001), "On Automorphism Groups of Cyclically Ordered Sets", Siberian Mathematical Journal 42 (1): 190–204, doi:10.1023/A:1004866131580. Translation of Tamarin (2001), "О группах автоморфизмов циклически упорядоченных множеств" (in Russian), Sibirskii Matematicheskii Zhurnal 42 (1): 212–230, http://mi.mathnet.ru/eng/smj1484, retrieved 30 April 2011
- Tararin, Valeri Mikhailovich (2002), "On c-3-Transitive Automorphism Groups of Cyclically Ordered Sets", Mathematical Notes 71 (1): 110–117, doi:10.1023/A:1013934509265. Translation of Tamarin (2002), "О c-3-транзитивных группах автоморфизмов циклически упорядоченных множеств", Matematicheskie Zametki 71 (1): 122–129, http://mi.mathnet.ru/eng/mz333, retrieved 22 May 2011
- Truss, John K. (2009), "On the automorphism group of the countable dense circular order", Fundamenta Mathematicae 204 (2): 97–111, doi:10.4064/fm204-2-1, http://www.maths.leeds.ac.uk/Pure/staff/truss/mnew.pdf, retrieved 25 April 2011
- Viro, Oleg; Ivanov, Oleg; Netsvetaev, Nikita; Kharlamov, Viatcheslav (2008), "8. Cyclic Orders", Elementary topology: problem textbook (1st English ed.), AMS Bookstore, pp. 42–44, ISBN 978-0-8218-4506-6, http://www.ams.org/bookstore/pspdf/mbk-54-prev.pdf, retrieved 25 April 2011
- Weinstein, Tilla (July 1996), An introduction to Lorentz surfaces, De Gruyter Expositions in Mathematics, 22, Walter de Gruyter, ISBN 978-3-11-014333-1
Further reading
- Bhattacharjee, Meenaxi; Macpherson, Dugald; Möller, Rögnvaldur G.; Neumann, Peter M. (1998), Notes on Infinite Permutation Groups, Lecture Notes in Mathematics, 1698, Springer, pp. 108–109, doi:10.1007/BFb0092550
- Bodirsky, Manuel; Pinsker, Michael (to appear), "Reducts of Ramsey Structures", Model Theoretic Methods in Finite Combinatorics, Contemporary Mathematics, AMS, arXiv:1105.6073
- Cameron, Peter J. (June 1976), "Transitivity of permutation groups on unordered sets", Mathematische Zeitschrift 148 (2): 127–139, doi:10.1007/BF01214702
- Cameron, Peter J. (June 1977), "Cohomological aspects of two-graphs", Mathematische Zeitschrift 157 (2): 101–119, doi:10.1007/BF01215145
- Cameron, Peter J. (1997), Evans, David M., ed., Model theory of groups and automorphism groups: Blaubeuren, August 1995, London Mathematical Society Lecture Note Series, 244, Cambridge University Press, pp. 126–133, ISBN 0-521-58955-X, http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.39.2321, retrieved 5 May 2011
- Courcelle, Joost; Engelfriet (April 2011), Graph Structure and Monadic Second-Order Logic, a Language Theoretic Approach, Cambridge University Press, http://www.labri.fr/perso/courcell/Book/TheBook.pdf, retrieved 17 May 2011
- Droste, M.; Giraudet, M.; Macpherson, D. (March 1995), "Periodic Ordered Permutation Groups and Cyclic Orderings", Journal of Combinatorial Theory, Series B 63 (2): 310–321, doi:10.1006/jctb.1995.1022
- Droste, M.; Giraudet, M.; Macpherson, D. (March 1997), "Set-Homogeneous Graphs and Embeddings of Total Orders", Order 14 (1): 9–20, doi:10.1023/A:1005880810385, http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.22.9135, retrieved 17 May 2011
- Evans, David M. (17 November 1997), "Finite covers with finite kernels", Annals of Pure and Applied Logic 88 (2–3): 109–147, doi:10.1016/S0168-0072(97)00018-3, http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.57.5323, retrieved 5 May 2011
- Ivanov, A. A. (January 1999), "Finite Covers, Cohomology and Homogeneous Structures", Proceedings of the London Mathematical Society 78 (1): 1–28, doi:10.1112/S002461159900163X
- Jakubík, Ján (2006), "On monotone permutations of ℓ-cyclically ordered sets", Czechoslovak Mathematical Journal 45 (2): 403–415, doi:10338.dmlcz/128075, http://dml.cz/bitstream/handle/10338.dmlcz/128075/CzechMathJ_56-2006-2_10.pdf, retrieved 30 April 2011
- Kennedy, Christine Cowan (August 1955), On a cyclic ternary relation ... (M.A. Thesis), Tulane University, OCLC 16508645
- Kónya, Eszter Herendine (2006), "A mathematical and didactical analysis of the concept of orientation", Teaching Mathematics and Computer Science 4 (1): 111–130, http://tmcs.math.klte.hu/Contents/2006-Vol-IV-Issue-I/konya-abstract.pdf, retrieved 17 May 2011
- Kónya, Eszter Herendine (2008), "Geometrical transformations and the concept of cyclic ordering", in Maj, Bożena; Pytlak, Marta; Swoboda, Ewa, Supporting Independent Thinking Through Mathematical Education, Rzeszów University Press, pp. 102–108, ISBN 978-83-7338-420-0, http://www.cme.rzeszow.pl/pdf/part_2_3.pdf, retrieved 17 May 2011
- Leloup, Gérard (February 2011), "Existentially equivalent cyclic ultrametric spaces and cyclically valued groups", Logic Journal of the IGPL 19 (1): 144–173, doi:10.1093/jigpal/jzq024, http://math.usask.ca/fvk/leloup3.pdf, retrieved 30 April 2011
- Marongiu, Gabriele (1985), "Some remarks on the ℵ0-categoricity of circular orderings" (in Italian), Unione Matematica Italiana. Bollettino. B. Serie VI 4 (3): 883–900, MR0831297
- McCleary, Stephen; Rubin, Matatyahu (6 October 2005), Locally Moving Groups and the Reconstruction Problem for Chains and Circles, arXiv:math/0510122
- Müller, G. (1974), "Lineare und zyklische Ordnung", Praxis der Mathematik 16: 261–269, MR0429660
- Rubin, M. (1996), "Locally moving groups and reconstruction problems", in Holland, W. Charles, Ordered groups and infinite permutation groups, Mathematics and Its Applications, 354, Kluwer, pp. 121–157, ISBN 978-0-7923-3853-6
- Świerczkowski, S. (1956), "On cyclic ordering relations", Bulletin de l'Académie Polonaise des Sciences, Classe III 4: 585–586
- Świerczkowski, S. (1959b), "On cyclically ordered intervals of integers", Fundamenta Mathematicae 47: 167–172, http://matwbn.icm.edu.pl/ksiazki/fm/fm47/fm4719.pdf, retrieved 2 May 2011
- Truss, J.K. (July 1992), "Generic Automorphisms of Homogeneous Structures", Proceedings of the London Mathematical Society s3-65 (1): 121–141, doi:10.1112/plms/s3-65.1.121
External links
- cyclic order at nLab
Categories:- Order theory
- Circles
- Combinatorics
Wikimedia Foundation. 2010.