Monotonic function

"Monotonicity" redirects here. For information on monotonicity as it pertains to voting systems, see monotonicity criterion.

"Monotonic" redirects here. For other uses, see Monotone (disambiguation).

Figure 1. A monotonically increasing function (it is strictly increasing on the left and right while just non-decreasing in the middle.)

Figure 2. A monotonically decreasing function.

Figure 3. A function that is not monotonic.

In mathematics, a monotonic function (or monotone function) is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory.

Monotonicity in calculus and analysis

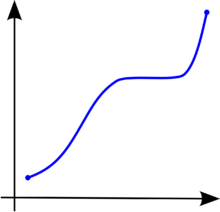
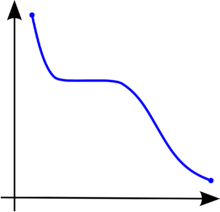
In calculus, a function f defined on a subset of the real numbers with real values is called monotonic (also monotonically increasing, increasing or non-decreasing), if for all x and y such that x ≤ y one has f(x) ≤ f(y), so f preserves the order (see Figure 1). Likewise, a function is called monotonically decreasing (also decreasing, or non-increasing) if, whenever x ≤ y, then f(x) ≥ f(y), so it reverses the order (see Figure 2).

If the order ≤ in the definition of monotonicity is replaced by the strict order <, then one obtains a stronger requirement. A function with this property is called strictly increasing. Again, by inverting the order symbol, one finds a corresponding concept called strictly decreasing. Functions that are strictly increasing or decreasing are one-to-one (because for x not equal to y, either x < y or x > y and so, by monotonicity, either f(x) < f(y) or f(x) > f(y), thus f(x) is not equal to f(y)).

When functions between discrete sets are considered in combinatorics, it is not always obvious that "increasing" and "decreasing" are taken to include the possibility of repeating the same value at successive arguments, so one finds the terms weakly increasing and weakly decreasing to stress this possibility.

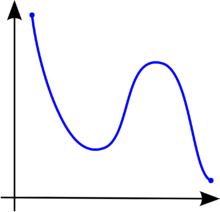
The terms "non-decreasing" and "non-increasing" should not be confused with the (much weaker) negative qualifications "not decreasing" and "not increasing". For example, the function of figure 3 first falls, then rises, then falls again. It is therefore not decreasing and not increasing, but it is neither non-decreasing nor non-increasing.

The term monotonic transformation can also possibly cause some confusion because it refers to a transformation by a strictly increasing function. Notably, this is the case in economics with respect to the ordinal properties of a utility function being preserved across a monotonic transform (see also monotone preferences).^[1]

A function f(x) is said to be absolutely monotonic over an interval (a, b) if the derivatives of all orders of f are nonnegative at all points on the interval.

Some basic applications and results

The following properties are true for a monotonic function f : R → R:

• f has limits from the right and from the left at every point of its domain;
• f has a limit at infinity (either ∞ or −∞) of either a real number, ∞, or −∞.
• f can only have jump discontinuities;
• f can only have countably many discontinuities in its domain.

These properties are the reason why monotonic functions are useful in technical work in analysis. Two facts about these functions are:

• if f is a monotonic function defined on an interval I, then f is differentiable almost everywhere on I, i.e. the set of numbers x in I such that f is not differentiable in x has Lebesgue measure zero.
• if f is a monotonic function defined on an interval [a, b], then f is Riemann integrable.

An important application of monotonic functions is in probability theory. If X is a random variable, its cumulative distribution function

F_X(x) = Prob(X ≤ x)

is a monotonically increasing function.

A function is unimodal if it is monotonically increasing up to some point (the mode) and then monotonically decreasing.

Monotonicity in functional analysis

In functional analysis on a topological vector space X, a (possibly non-linear) operator T : X → X^∗ is said to be a monotone operator if

$(Tu - Tv, u - v) \geq 0 \quad \forall u,v \in X.$

Kachurovskii's theorem shows that convex functions on Banach spaces have monotonic operators as their derivatives.

A subset G of X × X^∗ is said to be a monotone set if for every pair [u₁,w₁] and [u₂,w₂] in G,

$(w_1 - w_2, u_1 - u_2) \geq 0.$

G is said to be maximal monotone if it is maximal among all monotone sets in the sense of set inclusion. The graph of a monotone operator G(T) is a monotone set. A monotone operator is said to be maximal monotone if its graph is a maximal monotone set.

Monotonicity in order theory

In order theory, one does not restrict to real numbers, but one is concerned with arbitrary partially ordered sets or even with preordered sets. In these cases, the above definition of monotonicity is relevant as well. However, the terms "increasing" and "decreasing" are avoided, since they lose their appealing pictorial motivation as soon as one deals with orders that are not total. Furthermore, the strict relations < and > are of little use in many non-total orders and hence no additional terminology is introduced for them.

A monotone function is also called isotone, or order-preserving. The dual notion is often called antitone, anti-monotone, or order-reversing. Hence, an antitone function f satisfies the property

x ≤ y implies f(x) ≥ f(y),

for all x and y in its domain. It is easy to see that the composite of two monotone mappings is also monotone.

A constant function is both monotone and antitone; conversely, if f is both monotone and antitone, and if the domain of f is a lattice, then f must be constant.

Monotone functions are central in order theory. They appear in most articles on the subject and examples from special applications are found in these places. Some notable special monotone functions are order embeddings (functions for which x ≤ y if and only if f(x) ≤ f(y)) and order isomorphisms (surjective order embeddings).

Monotonicity in computer science

In computer science, monotonicity (also called consistency) is a condition applied to heuristic functions. A heuristic h(n) is monotonic if, for every node n and every successor n' of n generated by any action a, the estimated cost of reaching the goal from n is no greater than the step cost of getting to n' plus the estimated cost of reaching the goal from n' ,

$h(n) \leq c(n, a, n') + h(n').$

This is a form of triangle inequality, with n, n', and the goal G_n closest to n. Because every monotonic heuristic is also admissible, monotonicity is a stricter requirement than admissibility. In some heuristic algorithms, such as A*, the algorithm can be considered optimal if it is monotonic.^[2]

Boolean functions

In Boolean algebra, a monotonic function is one such that for all a_i and b_i in {0,1}, if a₁ ≤ b₁, a₂ ≤ b₂, ..., a_n ≤ b_n, then f(a₁, ... , a_n) ≤ f(b₁, ... , b_n). In other words, a Boolean function is monotonic if, for every combination of inputs, switching one of the inputs from false to true can only cause the output to switch from false to true and not from true to false. Graphically, this means that a Boolean function is monotonic when in its Hasse diagram (dual of its Venn diagram), there is no 1 (red vertex) connected to a higher 0 (white vertex).

The monotonic Boolean functions are precisely those that can be defined by an expression combining the inputs (which may appear more than once) using only the operators and and or (in particular not is forbidden). For instance "at least two of a,b,c hold" is a monotonic function of a,b,c, since it can be written for instance as ((a and b) or (a and c) or (b and c)).

The number of such functions on n variables is known as the Dedekind number of n.

Monotonic logic

Main article: Monotonicity of entailment

Monotonicity of entailment is a property of many logic systems that states that the hypotheses of any derived fact may be freely extended with additional assumptions. Any true statement in a logic with this property continues to be true, even after adding new axioms. Logics with this property may be called monotonic, to differentiate them from non-monotonic logic.

See also

• Monotone cubic interpolation
• Pseudo-monotone operator
• Total monotonicity

Notes

1. ^ See the section on Cardinal Versus Ordinal Utility in (Simon and Blume, 1994).
2. ^ Conditions for optimality: Admissibility and consistency pg. 94-95 (Russel and Norvig, 2010).

Bibliography

• Bartle, Robert G. (1976). The elements of real analysis (second edition ed.). 
• Grätzer, George (1971). Lattice theory: first concepts and distributive lattices. ISBN 0716704420. 
• Pemberton, Malcolm; Rau, Nicholas (2001). Mathematics for economists: an introductory textbook. Manchester University Press. ISBN 0719033411. 
• Renardy, Michael and Rogers, Robert C. (2004). An introduction to partial differential equations. Texts in Applied Mathematics 13 (Second edition ed.). New York: Springer-Verlag. pp. 356. ISBN 0-387-00444-0. 
• Riesz, Frigyes and Béla Szőkefalvi-Nagy (1990). Functional Analysis. Courier Dover Publications. ISBN 9780486662893. 
• Russell, Stuart J. and Norvig, Peter (2010). Artificial Intelligence: A Modern Approach (3rd ed.). Upper Saddle River, New Jersey: Prentice Hall. ISBN 9780136042594. 
• Simon, Carl P. and Lawrence Blume (April 1994). Mathematics for Economists (first edition ed.). ISBN 978-0393957334.  (Definition 9.31)

External links

• Convergence of a Monotonic Sequence by Anik Debnath and Thomas Roxlo (The Harker School), Wolfram Demonstrations Project.
• Definition of a Monotonic function from Wolfram Alpha