- Partially ordered set
-
In mathematics, especially order theory, a partially ordered set (or poset) formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the set, one of the elements precedes the other. Such a relation is called a partial order to reflect the fact that not every pair of elements need be related: for some pairs, it may be that neither element precedes the other in the poset. Thus, partial orders generalize the more familiar total orders, in which every pair is related. A finite poset can be visualized through its Hasse diagram, which depicts the ordering relation.
A familiar real-life example of a partially ordered set is a collection of people ordered by genealogical descendancy. Some pairs of people bear the descendant-ancestor relationship, but other pairs bear no such relationship.
Formal definition
A partial order is a binary relation "≤" over a set P which is reflexive, antisymmetric, and transitive, i.e., for all a, b, and c in P, we have that:
- a ≤ a (reflexivity);
- if a ≤ b and b ≤ a then a = b (antisymmetry);
- if a ≤ b and b ≤ c then a ≤ c (transitivity).
In other words, a partial order is an antisymmetric preorder.
A set with a partial order is called a partially ordered set (also called a poset). The term ordered set is sometimes also used for posets, as long as it is clear from the context that no other kinds of orders are meant. In particular, totally ordered sets can also be referred to as "ordered sets", especially in areas where these structures are more common than posets.
For a, b, elements of a partially ordered set P, if a ≤ b or b ≤ a, then a and b are comparable. Otherwise they are incomparable. A partial order under which every pair of elements is comparable is called a total order or linear order; a totally ordered set is also called a chain (e.g., the natural numbers with their standard order). A poset in which no two distinct elements are comparable is called an antichain.
Examples
Standard examples of posets arising in mathematics include:
- The real numbers ordered by the standard less-than-or-equal relation ≤ (a totally ordered set as well).
- The set of natural numbers equipped with the relation of divisibility.
- The vertex set of a directed acyclic graph ordered by reachability.
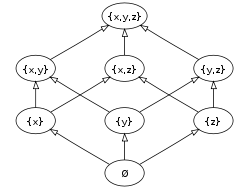
- The set of subsets of a given set (its power set) ordered by inclusion (see the figure on top-right).
- The set of subspaces of a vector space ordered by inclusion.
- For a partially ordered set P, the sequence space containing all sequences of elements from P, where sequence a precedes sequence b if every item in a precedes the corresponding item in b. Formally, (an)n∈ℕ ≤ (bn)n∈ℕ if and only if an ≤ bn for all n in ℕ.
- For a set X and a partially ordered set P, the function space containing all functions from X to P, where f ≤ g if and only if f(x) ≤ g(x) for all x in X.
- A fence, a partially ordered set defined by an alternating sequence of order relations a < b > c < d ...
Extrema
There are several notions of "greatest" and "least" element in a poset P, notably:
- Greatest element and least element: An element g in P is a greatest element if for every element a in P, a ≤ g. An element m in P is a least element if for every element a in P, a ≥ m. A poset can only have one greatest or least element.
- Maximal elements and minimal elements: An element g in P is a maximal element if there is no element a in P such that a > g. Similarly, an element m in P is a minimal element if there is no element a in P such that a < m. If a poset has a greatest element, it must be the unique maximal element, but otherwise there can be more than one maximal element, and similarly for least elements and minimal elements.
- Upper and lower bounds: For a subset A of P, an element x in P is an upper bound of A if a ≤ x, for each element a in A. In particular, x need not be in A to be an upper bound of A. Similarly, an element x in P is a lower bound of A if a ≥ x, for each element a in A. A greatest element of P is an upper bound of P itself, and a least element is a lower bound of P.
For example, consider the positive integers, ordered by divisibility: 1 is a least element, as it divides all other elements; on the other hand this poset does not have a greatest element (although if one would include 0 in the poset, which is a multiple of any integer, that would be a greatest element). This partially ordered set does not even have any maximal elements, since any g divides for instance 2g, which is distinct from it, so g is not be maximal. If we exclude the number 1, while keeping divisibility as ordering on the elements greater than 1, then the resulting poset does not have a least element, but any prime number is a minimal element for it. In this poset, 60 is an upper bound (though not a least upper bound) of the subset {2,3,5,10}, which subset does not have any lower bound (since 1 is not in the poset); on the other hand 2 is a lower bound of the subset of powers of 2, which subset does not have any upper bound.
Orders on the Cartesian product of partially ordered sets
In order of increasing strength, i.e., decreasing sets of pairs, three of the possible partial orders on the Cartesian product of two partially ordered sets are:
- Lexicographical order: (a,b) ≤ (c,d) if and only if a < c or (a = c and b ≤ d).
- (a,b) ≤ (c,d) if and only if a ≤ c and b ≤ d (the product order).
- (a,b) ≤ (c,d) if and only if (a < c and b < d) or (a = c and b = d) (the reflexive closure of the direct product of the corresponding strict orders).
All three can similarly be defined for the Cartesian product of more than two sets.
Applied to ordered vector spaces over the same field, the result is in each case also an ordered vector space.
See also orders on the Cartesian product of totally ordered sets.
Strict and non-strict partial orders
In some contexts, the partial order defined above is called a non-strict (or reflexive, or weak) partial order. In these contexts a strict (or irreflexive) partial order "<" is a binary relation that is irreflexive and transitive, and therefore asymmetric. In other words, asymmetric (hence irreflexive) and transitive.
Thus, for all a, b, and c in P, we have that:
- ¬(a < a) (irreflexivity);
- if a < b then ¬(b < a) (asymmetry); and
- if a < b and b < c then a < c (transitivity).
There is a 1-to-1 correspondence between all non-strict and strict partial orders.
If "≤" is a non-strict partial order, then the corresponding strict partial order "<" is the reflexive reduction given by:
- a < b if and only if (a ≤ b and a ≠ b)
Conversely, if "<" is a strict partial order, then the corresponding non-strict partial order "≤" is the reflexive closure given by:
- a ≤ b if and only if a < b or a = b.
This is the reason for using the notation "≤".
Strict partial orders are useful because they correspond more directly to directed acyclic graphs (dags): every strict partial order is a dag, and the transitive closure of a dag is both a strict partial order and also a dag itself.
Inverse and order dual
The inverse or converse ≥ of a partial order relation ≤ satisfies x≥y if and only if y≤x. The inverse of a partial order relation is reflexive, transitive, and antisymmetric, and hence itself a partial order relation. The order dual of a partially ordered set is the same set with the partial order relation replaced by its inverse. The irreflexive relation > is to ≥ as < is to ≤.
Any one of these four relations ≤, <, ≥, and > on a given set uniquely determine the other three.
In general two elements x and y of a partial order may stand in any of four mutually exclusive relationships to each other: either x < y, or x = y, or x > y, or x and y are incomparable (none of the other three). A totally ordered set is one that rules out this fourth possibility: all pairs of elements are comparable and we then say that trichotomy holds. The natural numbers, the integers, the rationals, and the reals are all totally ordered by their algebraic (signed) magnitude whereas the complex numbers are not. This is not to say that the complex numbers cannot be totally ordered; we could for example order them lexicographically via x+iy < u+iv if and only if x < u or (x = u and y < v), but this is not ordering by magnitude in any reasonable sense as it makes 1 greater than 100i. Ordering them by absolute magnitude yields a preorder in which all pairs are comparable, but this is not a partial order since 1 and i have the same absolute magnitude but are not equal, violating antisymmetry.
Number of partial orders
 Partially ordered set of set of all subsets of a six-element set {a, b, c, d, e, f}, ordered by the subset relation.
Partially ordered set of set of all subsets of a six-element set {a, b, c, d, e, f}, ordered by the subset relation.
Sequence A001035 in OEIS gives the number of partial orders on a set of n labeled elements:
Number of n-element binary relations of different types n all transitive reflexive preorder partial order total preorder total order equivalence relation 0 1 1 1 1 1 1 1 1 1 2 2 1 1 1 1 1 1 2 16 13 4 4 3 3 2 2 3 512 171 64 29 19 13 6 5 4 65536 3994 4096 355 219 75 24 15 OEIS A002416 A006905 A053763 A000798 A001035 A000670 A000142 A000110 The number of strict partial orders is the same as that of partial orders.
If we count only up to isomorphism, we get 1, 1, 2, 5, 16, 63, 318, … (sequence A000112 in OEIS).
Linear extension
A partial order ≤* on a set X is an extension of another partial order ≤ on X provided that for all elements x and y of X, whenever x ≤y, it is also the case that x ≤* y. A linear extension is an extension that is also a linear (i.e., total) order. Every partial order can be extended to a total order (order-extension principle).[1]
In computer science, algorithms for finding linear extensions of partial orders (represented as the reachability orders of directed acyclic graphs) are called topological sorting.
In category theory
Every poset (and every preorder) may be considered as a category in which every hom-set has at most one element. More explicitly, let hom(x, y) = {(x, y)} if x ≤ y (and otherwise the empty set) and (y, z)o(x, y) = (x, z). Posets are equivalent to one another if and only if they are isomorphic. In a poset, the smallest element, if any, is an initial object, and the largest element, if any, a terminal object. Also, every preordered set is equivalent to a poset. Finally, every subcategory of a poset is isomorphism-closed.
A functor from a poset category (a diagram indexed by a poset category) is a commutative diagram.
Partial orders in topological spaces
If P is a partially ordered set that has also been given the structure of a topological space, then it is customary to assume that {(a, b) a ≤ b} is a closed subset of the topological product space
 . Under this assumption partial order relations are well behaved at limits in the sense that if
. Under this assumption partial order relations are well behaved at limits in the sense that if  ,
,  and ai ≤ bi for all i, then a ≤ b.[2]
and ai ≤ bi for all i, then a ≤ b.[2]Interval
For a ≤ b, the closed interval [a,b] is the set of elements x satisfying a ≤ x ≤ b (i.e. a ≤ x and x ≤ b). It contains at least the elements a and b.
Using the corresponding strict relation "<", the open interval (a,b) is the set of elements x satisfying a < x < b (i.e. a < x and x < b). An open interval may be empty even if a < b. For example, the open interval (1,2) on the integers is empty since there are no integers i such that 1 < i < 2.
Sometimes the definitions are extended to allow a > b, in which case the interval is empty.
The half-open intervals [a,b) and (a,b] are defined similarly.
A poset is locally finite if every interval is finite. For example, the integers are locally finite under their natural ordering.
This concept of an interval in a partial order should not be confused with the particular class of partial orders known as the interval orders.
See also
- antimatroid, a formalization of orderings on a set that allows more general families of orderings than posets
- causal set
- comparability graph
- directed set
- graded poset
- semilattice
- lattice
- ordered group
- poset topology, a kind of topological space that can be defined from any poset
- semiorder
- series-parallel partial order
- strict weak ordering - strict partial order "<" in which the relation "neither a < b nor b < a" is transitive.
- complete partial order
Notes
- ^ Jech, Thomas (2008) [originally published in 1973]. The Axiom of Choice. Dover Publications. ISBN 0-486-46624-8.
- ^ L. E. Ward, Jr; Partially Ordered Topological Spaces; Proceedings of the American Mathematical Society, Vol. 5, No. 1 (Feb., 1954), pp. 144--161
References
- Jayant V. Deshpande, On Continuity of a Partial Order, Proceedings of the American Mathematical Society, Vol. 19, No. 2, 1968, pp. 383-386
- Bernd S. W. Schröder, Ordered Sets: An Introduction (Boston: Birkhäuser, 2003)
- Richard P. Stanley, Enumerative Combinatorics, vol.1, Cambridge Studies in Advanced Mathematics 49, Cambridge University Press, ISBN 0-521-66351-2
External links
Categories:- Order theory
- Mathematical relations
Wikimedia Foundation. 2010.