Reflexive relation

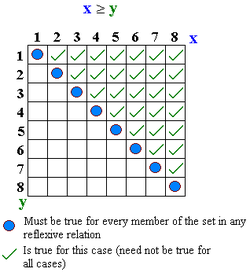
In mathematics, a reflexive relation is a binary relation on a set for which every element is related to itself, i.e., a relation ~ on S where x~x holds true for every x in S.^[1] For example, ~ could be "is equal to".

Related terms

An irreflexive, or anti-reflexive, relation is the opposite of a reflexive relation. It is a binary relation on a set where no element is related to itself. An example is the "greater than" relation (x>y). Note that not every relation which is not reflexive is irreflexive; it is possible to define relations where some elements are related to themselves but others are not related to themselves (i.e. neither all nor none). For example, the binary relation "the product of x and y is even" is reflexive on the set of even numbers, irreflexive on the set of odd numbers, and neither on the set of natural numbers.

A relation is called quasi-reflexive if every element that is related to some element is related to itself. An example is the relation "has the same limit as" on the set of sequences of real numbers: Not every sequence has a limit, and thus the relation is not reflexive, but if a sequence has the same limit as some sequence, then it has the same limit as itself.

The reflexive closure of a binary relation ~ on a set S is the smallest relation ~′ such that ~′ is a superset of ~ and ~′ is reflexive on S. This is equivalent to the union of ~ and the identity relation on S. For example, the reflexive closure of x<y is x≤y.

The reflexive reduction of a binary relation ~ on a set S is the smallest relation ~′ such that ~′ shares the same reflexive closure as ~. It can be seen in a way as the opposite of the reflexive closure. It is equivalent to the complement of the identity relation on S with regard to ~. That is, it is equivalent to ~ except for where x~x is true. For example, the reflexive reduction of x≤y is x<y.

Examples

Examples of reflexive relations include:

• "is equal to" (equality)
• "is a subset of" (set inclusion)
• "divides" (divisibility)
• "is greater/less than or equal to":

Examples of irreflexive relations include:

• "is not equal to"
• "is coprime to"(for the integers>1, since 1 is coprime to itself)
• "is a proper subset of"
• "is greater than"

Number of reflexive relations

The number of reflexive relations on an n-element set is 2ⁿ²⁻ⁿ.^[2]

Number of n-element binary relations of different types
n	all	transitive	reflexive	preorder	partial order	total preorder	total order	equivalence relation
0	1	1	1	1	1	1	1	1
1	2	2	1	1	1	1	1	1
2	16	13	4	4	3	3	2	2
3	512	171	64	29	19	13	6	5
4	65536	3994	4096	355	219	75	24	15
OEIS	A002416	A006905	A053763	A000798	A001035	A000670	A000142	A000110

See also

• Binary relation
• Symmetric relation
• Transitive relation

Notes

1. ^ Levy 1979:74
2. ^ On-Line Encyclopedia of Integer Sequences A053763

References

• Levy, A. (1979) Basic Set Theory, Perspectives in Mathematical Logic, Springer-Verlag. Reprinted 2002, Dover. ISBN 0-486-42079-5
• Lidl, R. and Pilz, G. (1998). Applied abstract algebra, Undergraduate Texts in Mathematics, Springer-Verlag. ISBN 0-387-98290-6
• Quine, W. V. (1951). Mathematical Logic, Revised Edition. Reprinted 2003, Harvard University Press. ISBN 0-674-55451-5