Coprime

In number theory, a branch of mathematics, two integers a and b are said to be coprime (also spelled co-prime) or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1.^[1] In addition to $\gcd(a, b) = 1\;$ and $(a, b) = 1,\;$ the notation a  $\perp$  b is sometimes used to indicate that a and b are relatively prime.^[2]

For example, 14 and 15 are coprime, being commonly divisible by only 1, but 14 and 21 are not, because they are both divisible by 7. The numbers 1 and −1 are coprime to every integer, and they are the only integers to be coprime with 0.

A fast way to determine whether two numbers are coprime is given by the Euclidean algorithm.

The number of integers coprime to a positive integer n, between 1 and n, is given by Euler's totient function (or Euler's phi function) φ(n).

Properties

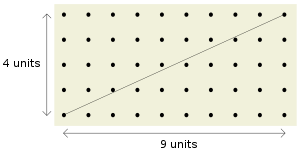Figure 1. The numbers 4 and 9 are coprime. Therefore, the diagonal of a 4 x 9 lattice does not intersect any other lattice points

There are a number of conditions which are equivalent to a and b being coprime:

• No prime number divides both a and b.
• There exist integers x and y such that ax + by = 1 (see Bézout's identity).
• The integer b has a multiplicative inverse modulo a: there exists an integer y such that by ≡ 1 (mod a). In other words, b is a unit in the ring Z/aZ of integers modulo a.
• Every pair of congruence relations for an unknown integer x, of the form x ≡ k (mod a) and x ≡ l (mod b), has a solution, as stated by the Chinese remainder theorem; in fact the solutions are described by a single congruence relation modulo ab.

As a consequence of the third point, if a and b are coprime and br ≡ bs (mod a), then r ≡ s (mod a) (because we may "divide by b" when working modulo a). Furthermore, if b₁ and b₂ are both coprime with a, then so is their product b₁b₂ (modulo a it is a product of invertible elements, and therefore invertible); this also follows from the first point by Euclid's lemma, which states that if a prime number p divides a product bc, then p divides at least one of the factors b, c.

As a consequence of the first point, if a and b are coprime, then so are any powers a^k and b^l.

If a and b are coprime and a divides the product bc, then a divides c. This can be viewed as a generalization of Euclid's lemma.

The two integers a and b are coprime if and only if the point with coordinates (a, b) in a Cartesian coordinate system is "visible" from the origin (0,0), in the sense that there is no point with integer coordinates between the origin and (a, b). (See figure 1.)

In a sense that can be made precise, the probability that two randomly chosen integers are coprime is 6/π² (see pi), which is about 61%. See below.

Two natural numbers a and b are coprime if and only if the numbers 2^a − 1 and 2^b − 1 are coprime. As a generalization of this, following easily from Euclidean algorithm in base n > 1:

gcd(n^a − 1,n^b − 1) = n^gcd(a,b) − 1.

Cross notation, group

If n≥1 and is an integer, the numbers coprime to n, taken modulo n, form a group with multiplication as operation; it is written as (Z/nZ)^× or Z_n^*.

Generalizations

Two ideals A and B in the commutative ring R are called coprime (or comaximal) if A + B = R. This generalizes Bézout's identity: with this definition, two principal ideals (a) and (b) in the ring of integers Z are coprime if and only if a and b are coprime.

If the ideals A and B of R are coprime, then AB = A∩B; furthermore, if C is a third ideal such that A contains BC, then A contains C. The Chinese remainder theorem is an important statement about coprime ideals.

The concept of being relatively prime can also be extended to any finite set of integers S = {a₁, a₂, .... a_n} to mean that the greatest common divisor of the elements of the set is 1. If every pair in a (finite or infinite) set of integers is relatively prime, then the set is called pairwise relatively prime.

Every pairwise relatively prime finite set is relatively prime; however, the converse is not true: {6, 10, 15} is relatively prime, but not pairwise relative prime (in fact, each pair of integers in the set has a non-trivial common factor).

Probabilities

Given two randomly chosen integers A and B, it is reasonable to ask how likely it is that A and B are coprime. In this determination, it is convenient to use the characterization that A and B are coprime if and only if no prime number divides both of them (see Fundamental theorem of arithmetic).

Intuitively, the probability that any number is divisible by a prime (or any integer), p is 1 / p (for example, every 7th integer is divisible by 7.) Hence the probability that two numbers are both divisible by this prime is 1 / p², and the probability that at least one of them is not is 1 − 1 / p². Now, for distinct primes, these divisibility events are mutually independent. (This would not, in general, be true if they were not prime.) (For the case of two events, a number is divisible by p and q if and only if it is divisible by pq; the latter has probability 1/pq.) Thus the probability that two numbers are coprime is given by a product over all primes,

$\prod_p^{\infty} \left(1-\frac{1}{p^2}\right) = \left( \prod_p^{\infty} \frac{1}{1-p^{-2}} \right)^{-1} = \frac{1}{\zeta(2)} = \frac{6}{\pi^2} \approx 0.607927102 \approx 61%.$

Here ζ refers to the Riemann zeta function, the identity relating the product over primes to ζ(2) is an example of an Euler product, and the evaluation of ζ(2) as π²/6 is the Basel problem, solved by Leonhard Euler in 1735. In general, the probability of k randomly chosen integers being coprime is 1/ζ(k).

There is often confusion about what a "randomly chosen integer" is. One way of understanding this is to assume that the integers are chosen randomly between 1 and an integer N. Then, for each upper bound N, there is a probability P_N that two randomly chosen numbers are coprime. This will never be exactly 6 / π², but in the limit as $N \to \infty$, $P_N \to 6/\pi^2$.^[3]

Generating all coprime pairs

All pairs of coprime numbers m,n can be generated in a parent-3 children-9 grandchildren... family tree starting from (2,1) (for even-odd or odd-even pairs)^[4] or from (3,1) (for odd-odd pairs),^[5] with three branches from each node. The branches are generated as follows:

Branch 1: m_next = 2m − n, and n_next = m

Branch 2: m_next = 2m + n, and n_next = m

Branch 3: m_next = m + 2n, and n_next = n

This family tree is exhaustive and non-redundant with no invalid members.

References

1. ^ G.H. Hardy; E. M. Wright (2008). An Introduction to the Theory of Numbers (6th ed. ed.). Oxford University Press. p. 6. ISBN 9780199219865. 
2. ^ Graham, R. L.; Knuth, D. E.; Patashnik, O. (1989), Concrete Mathematics, Addison-Wesley 
3. ^ This theorem was proved by Ernesto Cesàro in 1881. For a more rigorous proof than the intuitive and informal one given here, see G.H. Hardy; E. M. Wright (2008). An Introduction to the Theory of Numbers (6th ed. ed.). Oxford University Press. ISBN 9780199219865. , theorem 332.
4. ^ Saunders, Robert & Randall, Trevor (July 1994), "The family tree of the Pythagorean triplets revisited", Mathematical Gazette 78: 190–193 .
5. ^ Mitchell, Douglas W. (July 2001), "An alternative characterisation of all primitive Pythagorean triples", Mathematical Gazette 85: 273–275 .

Further reading

• Lord, Nick (March 2008), "A uniform construction of some infinite coprime sequences", Mathematical Gazette 92: 66–70 .