Michaelis–Menten kinetics

An example curve with parameters V_max=3.4 and K_m=0.4.

In biochemistry, Michaelis–Menten kinetics is one of the simplest and best-known models of enzyme kinetics. It is named after German biochemist Leonor Michaelis and Canadian physician Maud Menten. The model takes the form of an equation describing the rate of enzymatic reactions, by relating reaction rate v to [S], the concentration of a substrate S. Its formula is given by

$v = \frac{ V_\max {[S]}}{K_m + [S]}.$

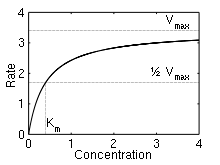
Here, V_max  represents the maximum rate achieved by the system, at maximum (saturating) substrate concentrations. The Michaelis constant K_m is the substrate concentration at which the reaction rate is half of V_max . Biochemical reactions involving a single substrate are often assumed to follow Michaelis–Menten kinetics, without regard to the model's underlying assumptions.

Model

Change in concentrations over time for enzyme E, substrate S, complex ES and product P

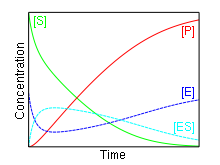
In 1903, French physical chemist Victor Henri found that enzyme reactions were initiated by a bond between the enzyme and the substrate.^[1] His work was taken up by German biochemist Leonor Michaelis and Canadian physician Maud Menten who investigated the kinetics of an enzymatic reaction mechanism, invertase, that catalyzes the hydrolysis of sucrose into glucose and fructose.^[2] In 1913, they proposed a mathematical model of the reaction.^[3] It involves an enzyme E binding to a substrate S to form a complex ES, which in turn is converted into a product P and the enzyme. This may be represented schematically as

$E + S \, \overset{k_f}\underset{k_r} \rightleftharpoons \, ES \, \overset{k_{cat}} {\longrightarrow} \, E + P$

where k_f, k_r and k_cat denote the rate constants,^[4] and the double arrows between S and ES represent the fact that enzyme-substrate binding is a reversible process.

Under certain assumptions – such as the enzyme concentration being much less than the substrate concentration – the rate of product formation is given by

$v = V_\max \frac{[S]}{K_m + [S]} = k_\text{cat} [E]_0 \frac{[S]}{K_m + [S]}.$

The reaction rate increases with increasing substrate concentration [S], asymptotically approaching its maximum rate V_max , attained when all enzyme is bound to substrate. It also follows that V_max  = k_cat[E]₀, where [E]₀ is the enzyme concentration. k_cat, the turnover number, is maximum number of substrate molecules converted to product per enzyme molecule per second.

The Michaelis constant K_m is the substrate concentration at which the reaction rate is at half-maximum, and is a measure of the substrate's affinity for the enzyme. A small K_m indicates high affinity, meaning that the rate will approach V_max  more quickly.^[5]

The model is used in a variety of biochemical situations other than enzyme-substrate interaction, including antigen-antibody binding, DNA-DNA hybridization and protein-protein interaction.^[5][6] It can be used to characterise a generic biochemical reaction, in the same way that the Langmuir equation can be used to model generic adsorption of biomolecular species.^[6]

Applications

Parameter values vary wildly between enzymes:^[7]

Enzyme	Km (M)	kcat (1/s)	kcat / Km (1/M.s)
Chymotrypsin	1.5 × 10-2	0.14	9.3
Pepsin	3.0 × 10-4	0.50	1.7 × 103
Tyrosyl-tRNA synthetase	9.0 × 10-4	7.6	8.4 × 103
Ribonuclease	7.9 × 10-3	7.9 × 102	1.0 × 105
Carbonic anhydrase	2.6 × 10-2	4.0 × 105	1.5 × 107
Fumarase	5.0 × 10-6	8.0 × 102	1.6 × 108

The constant k_cat / K_m is a measure of how efficiently an enzyme converts a substrate into product. It has a theoretical upper limit of 10⁸ – 10¹⁰ /M.s; enzymes working close to this, such as fumarase, are termed superefficient.^[8]

Michaelis-Menten kinetics have also been applied to a variety of spheres outside of biochemical reactions,^[4] including alveolar clearance of dusts,^[9] the richness of species pools,^[10] clearance of blood alcohol,^[11] the photosynthesis-irradiance relationship and bacterial phage infection.^[12]

Derivation

Applying the law of mass action, which states that the rate of a reaction is proportional to the product of the concentrations of the reactants, gives a system of four non-linear ordinary differential equations that define the rate of change of reactants with time t:^[13]

$\begin{array}{ccccc} d [S] / d t & = & - k_f [E] [S] & + k_r [ES] & \\ d [E] / d t & = & - k_f [E] [S] & + k_r [ES] & + k_{cat} [ES] \\ d [ES] / d t & = & + k_f [E] [S] & - k_r [ES] & - k_{cat} [ES] \\ d [P] / d t & = & & & + k_{cat} [ES] \\ \end{array}$

In this mechanism, the enzyme E is a catalyst, which only facilitates the reaction, so its total concentration, free plus combined, [E] + [ES] = [E]₀ is a constant. This conservation law can also be obtained by adding the second and third equations above.^[13][14]

Equilibrium approximation

In their original analysis, Michaelis and Menten assumed that the substrate is in instantaneous chemical equilibrium with the complex, and thus k_f[E][S] = k_r[ES].^[3][14] Combining this relationship with the enzyme conservation law, the concentration of complex is^[14]

$[ES] = \frac{[E]_0 [S]}{K_d + [S]}$

where K_d = k_r / k_f is the dissociation constant for the enzyme-substrate complex. Hence the velocity v of the reaction – the rate at which P is formed – is^[14]

$v = d [P]/d t = \frac{V_\max {[S]}}{K_d + [S]}$

where V_max  = k_cat[E]₀ is the maximum reaction velocity.

Quasi-steady-state approximation

An alternative analysis of the system was undertaken by British botanist G. E. Briggs and British geneticist J. B. S. Haldane in 1925.^[15] They assumed that the concentration of the intermediate complex does not change on the time-scale of product formation – known as the quasi-steady-state assumption or pseudo-steady-state-hypothesis. Mathematically, this assumption means k_f[E][S] = k_r[ES] + k_cat[ES]. Combining this relationship with the enzyme conservation law, the concentration of complex is^[14]

$[ES] = \frac{[E]_0 [S]}{K_m + [S]}$

where

$K_m = \frac{k_r + k_{cat}}{k_f}$

is known as the Michaelis constant. Hence the velocity v of the reaction is^[14]

$v = d [P]/d t = \frac{V_\max {[S]}}{K_m + [S]}.$

Assumptions and limitations

The first step in the derivation applies the law of mass action, which is reliant on free diffusion. However, in the environment of a living cell where there is a high concentration of protein, the cytoplasm often behaves more like a gel than a liquid, limiting molecular movements and altering reaction rates.^[16] Whilst the law of mass action can be valid in heterogeneous environments,^[17] it is more appropriate to model the cytoplasm as a fractal, in order to capture its limited-mobility kinetics.^[18]

The resulting reaction rates predicted by the two approaches are similar, with the only difference being that the equilibrium approximation defines the constant as K_d, whilst the quasi-steady-state approximation uses K_m. However, each approach is founded upon a different assumption. The Michaelis-Menten equilibrium analysis is valid if the substrate reaches equilibrium on a much faster time-scale than the product is formed or, more precisely, that ^[14]

$\epsilon_d = \frac{k_{cat}}{k_r} \ll 1$

By contrast, the Briggs-Haldane quasi-steady-state analysis is valid if ^[13][19]

$\epsilon_m = \frac{[E]_0}{[S]_0 + K_m} \ll 1$

Thus it holds if the enzyme concentration is much less than the substrate concentration. Even if this is not satisfied, the approximation is valid if K_m is large.

In both the Michaelis-Menten and Briggs-Haldane analyses, the quality of the approximation improves as $\epsilon\,\!$ decreases. However, in model building, Michaelis-Menten kinetics are often invoked without regard to the underlying assumptions.^[14]

Determination of constants

The typical method for determining the constants V_max  and K_m involves running a series of enzyme assays at varying substrate concentrations [S], and measuring the initial reaction rate v₀. 'Initial' here is taken to mean that the reaction rate is measured after a relatively short time period, during which it is assumed that the enzyme-substrate complex has formed, but that the substrate concentration held approximately constant, and so the equilibrium or quasi-steady-state approximation remain valid.^[19] By plotting reaction rate against concentration, and using nonlinear regression of the Michaelis-Menten equation, the parameters may be obtained.^[20]

Before computing facilities to perform nonlinear regression became available, graphical methods involving linearisation of the equation were used. A number of these were proposed, including the Eadie–Hofstee diagram, Hanes–Woolf plot and Lineweaver–Burk plot; of these, the Hanes-Woolf plot is the most accurate.^[20] However, while useful for visualization, all three methods distort the error structure of the data and are inferior to nonlinear regression.^[21] Nonetheless, their use can still be found in modern literature.^[22]

References

1. ^ Henri, Victor (1903). Lois Générales de l’Action des Diastases. Paris: Hermann.  Google books (US only)
2. ^ "Victor Henri". Whonamedit?. http://www.whonamedit.com/doctor.cfm/2881.html. Retrieved 24 May 2011. 
3. ^ ^{a b} Menten, L.; Michaelis, M.I. (1913), "Die Kinetik der Invertinwirkung", Biochem Z 49: 333–369  (recent translation, and an older partial translation)
4. ^ ^{a b} Chen, W.W.; Neipel, M.; Sorger, P.K. (2010). "Classic and contemporary approaches to modeling biochemical reactions". Genes Dev 24 (17): 1861–1875. doi:10.1101/gad.1945410. PMC 2932968. PMID 20810646. http://www.pubmedcentral.nih.gov/articlerender.fcgi?tool=pmcentrez&artid=2932968. 
5. ^ ^{a b} Lehninger, A.L.; Nelson, D.L.; Cox, M.M. (2005). Lehninger principles of biochemistry. New York: W.H. Freeman. ISBN 978-0-7167-4339-2. 
6. ^ ^{a b} Chakraborty, S. (23 Dec 2009). Microfluidics and Microfabrication (1 ed.). Springer. ISBN 978-1441915429. 
7. ^ Mathews, C.K.; van Holde, K.E.; Ahern, K.G. (10 Dec 1999). Biochemistry (3 ed.). Prentice Hall. ISBN 978-0805330663. http://www.pearsonhighered.com/mathews/. 
8. ^ Stroppolo, M.E.; Falconi, M.; Caccuri, A.M.; Desideri, A. (Sep 2001). "Superefficient enzymes". Cell Mol Life Sci 58 (10): 1451–60. doi:10.1007/PL00000788. PMID 11693526. 
9. ^ Yu, R.C.; Rappaport, S.M. (1997). "A lung retention model based on Michaelis-Menten-like kinetics". Environ Health Perspect 105 (5): 496–503. doi:10.1289/ehp.97105496. PMC 1469867. PMID 9222134. http://www.pubmedcentral.nih.gov/articlerender.fcgi?tool=pmcentrez&artid=1469867. 
10. ^ Keating, K.A.; Quinn, J.F. (1998). "Estimating species richness: the Michaelis-Menten model revisited". Oikos 81 (2): 411–416. doi:10.2307/3547060. JSTOR 3547060. 
11. ^ Jones, A.W. (2010). "Evidence-based survey of the elimination rates of ethanol from blood with applications in forensic casework". Forensic Sci Int 200 (1–3): 1–20. doi:10.1016/j.forsciint.2010.02.021. PMID 20304569. 
12. ^ Abedon, S.T. (2009). "Kinetics of phage-mediated biocontrol of bacteria". Foodborne Pathog Dis 6 (7): 807–15. doi:10.1089/fpd.2008.0242. PMID 19459758. 
13. ^ ^{a b c} Murray, J.D. (2002). Mathematical Biology: I. An Introduction (3 ed.). Springer. ISBN 978-0387952239. 
14. ^ ^{a b c d e f g h} Keener, J.; Sneyd, J. (2008). Mathematical Physiology: I: Cellular Physiology (2 ed.). Springer. ISBN 978-0387758466. 
15. ^ Briggs, G.E.; Haldane, J.B.S. (1925). "A note on the kinematics of enzyme action". Biochem J 19 (2): 338–339. PMC 1259181. PMID 16743508. http://www.pubmedcentral.nih.gov/articlerender.fcgi?tool=pmcentrez&artid=1259181. 
16. ^ Zhou, H.X.; Rivas, G.; Minton, A.P. (2008). "Macromolecular crowding and confinement: biochemical, biophysical, and potential physiological consequences". Annu Rev Biophys 37: 375–97. doi:10.1146/annurev.biophys.37.032807.125817. PMC 2826134. PMID 18573087. http://www.pubmedcentral.nih.gov/articlerender.fcgi?tool=pmcentrez&artid=2826134. 
17. ^ Grima, R.; Schnell, S. (Oct 2006). "A systematic investigation of the rate laws valid in intracellular environments". Biophys Chem 124 (1): 1–10. doi:10.1016/j.bpc.2006.04.019. PMID 16781049. 
18. ^ Schnell, S.; Turner, T.E. (2004). "Reaction kinetics in intracellular environments with macromolecular crowding: simulations and rate laws". Prog Biophys Mol Biol 85 (2–3): 235–60. doi:10.1016/j.pbiomolbio.2004.01.012. PMID 15142746. 
19. ^ ^{a b} Segel, L.A.; Slemrod, M. (1989). "The quasi-steady-state assumption: A case study in perturbation". Thermochim Acta 31 (3): 446–477. doi:10.1137/1031091. 
20. ^ ^{a b} Leskovac, V. (2003). Comprehensive enzyme kinetics. New York: Kluwer Academic/Plenum Pub.. ISBN 978-0-306-46712-7. 
21. ^ Greco, W.R.; Hakala, M.T. (1979). "Evaluation of methods for estimating the dissociation constant of tight binding enzyme inhibitors,". J Biol Chem 254 (23): 12104–12109. PMID 500698. 
22. ^ Hayakawa, K.; Guo, L.; Terentyeva, E.A.; Li, X.K.; Kimura, H.; Hirano, M.; Yoshikawa, K.; Nagamine, T. et al. (2006). "Determination of specific activities and kinetic constants of biotinidase and lipoamidase in LEW rat and Lactobacillus casei (Shirota)". J Chromatogr B Analyt Technol Biomed Life Sci 844 (2): 240–50. doi:10.1016/j.jchromb.2006.07.006. PMID 16876490. 

Further reading

• Biochemistry/Catalysis at Wikibooks