Quadrupole ion trap

Scheme of a Quadrupole ion trap of classical setup with a particle of positive charge (dark red), surrounded by a cloud of similarly charged particles (light red). The electric field E (blue) is generated by a quadrupole of endcaps (a, positive) and a ring electrode (b). Picture 1 and 2 show two states during an AC cycle.

A quadrupole ion trap exists in both linear and 3D (Paul Trap, QIT) varieties and refers to an ion trap that uses constant DC and radio frequency (RF) oscillating AC electric fields to trap ions. It is commonly used as a component of a mass spectrometer. The invention of the 3D quadrupole ion trap itself is attributed to Wolfgang Paul who shared the Nobel Prize in Physics in 1989 for this work.^[1][2]

Theory

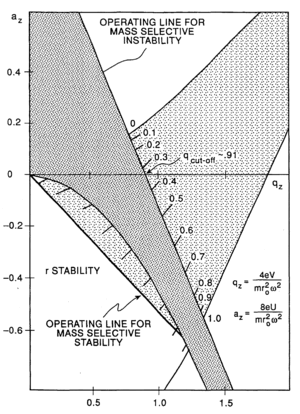
The 3D trap itself generally consists of two hyperbolic metal electrodes with their foci facing each other and a hyperbolic ring electrode halfway between the other two electrodes. The ions are trapped in the space between these three electrodes by AC (oscillating, non-static) and DC (non-oscillating, static) electric fields. The AC radio frequency voltage oscillates between the two hyperbolic metal end cap electrodes if ion excitation is desired; the driving AC voltage is applied to the ring electrode. The ions are first pulled up and down axially while being pushed in radially. The ions are then pulled out radially and pushed in axially (from the top and bottom). In this way the ions move in a complex motion that generally involves the cloud of ions being long and narrow and then short and wide, back and forth, oscillating between the two states. Since the mid-1980s most 3D traps (Paul traps) have used ~1 mtorr of helium. The use of damping gas and the mass-selective instability mode developed by Stafford et al. led to the first commercial 3D ion traps.^[3]

Linear Ion Trap at the University of Calgary

The quadrupole ion trap has two configurations: the three dimensional form described above and the linear form made of 4 parallel electrodes. A simplified rectilinear configuration has also been used.^[4] The advantage of the linear design is in its simplicity, but this leaves a particular constraint on its modeling. To understand how this originates, it is helpful to visualize the linear form. The Paul trap is designed to create a saddle-shaped field to trap a charged ion, but with a quadrupole, this saddle-shaped electric field cannot be rotated about an ion in the centre. It can only 'flap' the field up and down. For this reason, the motions of a single ion in the trap are described by the Mathieu Equations. These equations can only be solved numerically, or equivalently by computer simulations.

The intuitive explanation and lowest order approximation is the same as strong focusing in accelerator physics. Since the field affects the acceleration, the position lags behind (to lowest order by half a period). So the particles are at defocused positions when the field is focusing and vice versa. Being farther from center, they experience a stronger field when the field is focusing than when it is defocusing.

Equations of motion

Ions in a quadrupole field experience restoring forces that drive them back toward the center of the trap. The motion of the ions in the field is described by solutions to the Mathieu equation.^[5] When written for ion motion in a trap, the equation is

$\frac{d^2u}{d\xi^2}+[a_u-2q_u\cos (2\xi) ]u=0 \qquad\qquad (1) \!$

where u represents the x, y and z coordinated, ξ is a dimensionless parameter given by $\xi=\Omega t/2\$, and $a_u\,$ and $q_u\,$ are dimensionless trapping parameters. The parameter $\Omega\,$ is the radial frequency of the potential applied to the ring electrode. By substituting the expression for ξ into Equation 1, it can be shown that

$\frac{d^2u}{dt^2} = \frac{\Omega^2}{4} \frac{d^2u}{d\xi^2} \qquad\qquad (2) \!$

Substituting Equation 2 into the Matthieu Equation 1 yields

$\frac{4}{\Omega^2}\frac{d^2u}{dt^2} + [a_u-2q_u\cos (\Omega t) ]u=0 \qquad\qquad (3) \!$.

Reorganizing terms shows us that

$m \frac{d^2u}{dt^2} + m \frac{\Omega^2}{4}[a_u-2q_u\cos (\Omega t) ]u=0 \qquad\qquad (3) \!$.

By Newton's laws of motion, the above equation represents the force on the ion. This equation can be exactly solved using Floquet theorem or the standard techniques of multiple scale analysis ^[6]. The particle dynamics and time averaged density of charged particles in a Paul trap can also be obtained by the concept of ponderomotive force.

The forces in each dimension are not coupled, thus the force acting on an ion in, for example, the x dimension is

$F_x = ma = m\frac{d^2x}{dt^2} = -e \frac{\partial \phi}{\partial x} \qquad\qquad (4) \!$

Here, $\phi\,$ is the quadrupolar potential, given by

$\phi=\frac{\phi_0}{r_0^2} \big( \lambda x^2 + \sigma y^2 + \gamma z^2 \big) \qquad\qquad (5) \!$

where $\phi _0\,$ is the applied electric potential and $\lambda\,$, $\sigma\,$, and $\gamma\,$ are weighting factors, and $r_0\,$ is a size parameter constant. In order to satisfy the Laplace Condition, $\nabla^2\phi_0=0\,$, it can be shown that

$\lambda + \sigma + \gamma =0 \,$.

For an ion trap, $\lambda = \sigma =1 \,$ and $\gamma =-2 \,$ and for a quadrupole mass filter, $\lambda = -\sigma =1 \,$ and $\gamma =0 \,$.

Transforming Equation 5 into a cylindrical coordinate system with ${x}={r} \,\cos\theta$, ${y}={r} \, \sin\theta$, and ${z}={z} \,$ and applying the pythagorean trigonometric identity $\sin^2 \theta + \cos^2 \theta = 1 \,$ gives

Diagram of the stability regions of a quadrupole ion trap according to the voltage and frequency applied to the ion trap elements.

$\phi_{r,z} = \frac{\phi_0}{r_0^2} \big( r^2 - 2z^2 \big) . \qquad\qquad (6) \!$

The applied electric potential is a combination of RF and DC given by

$\phi_0 = U + V\cos \Omega t .\qquad\qquad (7) \!$

where Ω = 2πν and ν is the applied frequency in hertz.

Substituting Equation 7 into Equation 5 with λ = 1 gives

$\frac{\partial \phi}{\partial x} = \frac {2x}{r_0^2} \big( U + V\cos \Omega t \big) . \qquad\qquad (8) \!$

Substituting Equation 8 into Equation 4 leads to

$m\frac {d^2x}{dt^2} = - \frac {2e}{r_0^2} \big( U + V\cos \Omega t \big) x . \qquad\qquad (9) \!$

Comparing terms on the right hand side of Equation 1 and Equation 9 leads to

$a_x = \frac {8eU} {m r_0^2 \Omega^2} \qquad\qquad (10) \!$

and

$q_x = - \frac {4eV} {m r_0^2 \Omega^2} . \qquad\qquad (11) \!$

Further $q_x = q_y\,$,

$a_z = -\frac {8eU} {m r_0^2 \Omega^2} \qquad\qquad (12) \!$

and

$q_z = \frac {4eV} {m r_0^2 \Omega^2} . \qquad\qquad (13) \!$

The trapping of ions can be understood in terms of stability regions in q_u and a_u space.

Linear ion trap

LTQ (Linear trap quadrupole)

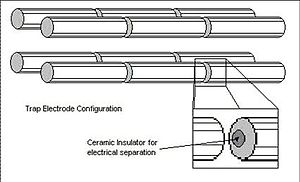
The linear ion trap uses a set of quadrupole rods to confine ions radially and a static electrical potential on-end electrodes to confine the ions axially.^[7] The linear form of the trap can be used as a selective mass filter, or as an actual trap by creating a potential well for the ions along the axis of the electrodes.^[8] Advantages of the linear trap design are increased ion storage capacity, faster scan times, and simplicity of construction (although quadrupole rod alignment is critical, adding a quality control constraint to their production. This constraint is additionally present in the machining requirements of the 3D trap).^[9]

Cylindrical ion trap

Cylindrical ion traps have a cylindrical rather than a hyperbolic ring electrode.^{[10][11][12][13]} This configuration has been used in miniature arrays of traps.

References

1. ^ Paul W., Steinwedel H. (1953). "Ein neues Massenspektrometer ohne Magnetfeld". RZeitschrift für Naturforschung A 8 (7): 448-450
2. ^ DE 944900  "Verfahren zur Trennung bzw. zum getrennten Nachweis von Ionen verschiedener spezifischer Ladung", W. Paul and H. Steinwedel, filed on December 24, 1953, priority December 23, 1953
3. ^ Stafford, G. C.; P. E. Kelley, J. E. P. Syka, W. E. Reynolds and J. F. J. Todd (7 September 1984). "Recent improvements in and analytical applications of advanced ion trap technology". International Journal of Mass Spectrometry and Ion Processes (Elsevier Science B.V.) 60 (1): 85–98. doi:10.1016/0168-1176(84)80077-4. 
4. ^ Ouyang Z, Wu G, Song Y, Li H, Plass WR, Cooks RG (August 2004). "Rectilinear ion trap: concepts, calculations, and analytical performance of a new mass analyzer". Anal. Chem. 76 (16): 4595–605. doi:10.1021/ac049420n. PMID 15307768. 
5. ^ March, Raymond (1997). "An Introduction to Quadrupole Ion Trap Mass Spectrometry". Journal of Mass Spectrometry 32 (4): 351–369. doi:10.1002/(SICI)1096-9888(199704)32:4<351::AID-JMS512>3.0.CO;2-Y. |url=http://www.spectroscopynow.com/FCKeditor/UserFiles/File/specNOW/jms32351.pdf%7Cformat=PDF%7Caccessdate=2008-05-06
6. ^ N. W. McLachlan, Theory and Applications of Mathieu Functions (Oxford University Press, Oxford, 1947), p. 20
7. ^ Douglas DJ, Frank AJ, Mao D (2005). "Linear ion traps in mass spectrometry". Mass spectrometry reviews 24 (1): 1–29. doi:10.1002/mas.20004. PMID 15389865. 
8. ^ Quadrupole ion trap mass spectrometry: a view at the turn of the century, Raymond E. March, International Journal of Mass Spectrometry 200, 2000, pp.285-312
9. ^ Schwartz, Jae C.; Michael W. Senko and John E. P. Syka (June 2002). "A two-dimensional quadrupole ion trap mass spectrometer". Journal of the American Society for Mass Spectrometry (Elsevier Science B.V.) 13 (6): 659–669. doi:10.1016/S1044-0305(02)00384-7. PMID 12056566. 
10. ^ Ouyang Z, Badman ER, Cooks RG (1999). "Characterization of a serial array of miniature cylindrical ion trap mass analyzers". Rapid Communications in Mass Spectrometry 13 (24): 2444–9. doi:10.1002/(SICI)1097-0231(19991230)13:24<2444::AID-RCM810>3.0.CO;2-F. PMID 10589092. 
11. ^ Patterson GE, Guymon AJ, Riter LS, Everly M, Griep-Raming J, Laughlin BC, Ouyang Z, Cooks RG (2002). "Miniature cylindrical ion trap mass spectrometer". Anal. Chem. 74 (24): 6145–53. doi:10.1021/ac020494d. PMID 12510732. 
12. ^ Kanawati B, Wanczek KP (2007). "Characterization of a new open cylindrical ion cyclotron resonance cell with unusual geometry". The Review of scientific instruments 78 (7): 074102. Bibcode 2007RScI...78g4102K. doi:10.1063/1.2751100. PMID 17672776. 
13. ^ Cruz D, Chang JP, Fico M, Guymon AJ, Austin DE, Blain MG (2007). "Design, microfabrication, and analysis of micrometer-sized cylindrical ion trap arrays". The Review of scientific instruments 78 (1): 015107. Bibcode 2007RScI...78a5107C. doi:10.1063/1.2403840. PMID 17503946. 

Bibliography

• W. Paul Electromagnetic Traps for Charged and Neutral Particles Taken from Proceedings of the International School of Physics <<Enrico Fermi>> Course CXVIII “Laser Manipulation of Atoms and Ions”, (North Holland, New York, 1992) p. 497-517
• R.I. Thompson, T.J. Harmon, and M.G. Ball, The rotating-saddle trap: a mechanical analogy to RF-electric-quadrupole ion trapping? (Canadian Journal of Physics, 2002: 80 12) p. 1433–1448
• M. Welling, H.A. Schuessler, R.I. Thompson, H. Walther Ion/Molecule Reactions, Mass Spectrometry and Optical Spectroscopy in a Linear Ion Trap (International Journal of Mass Spectrometry and Ion Processes, 1998: 172) p. 95-114.
• G. Werth (2005). Charged Particle Traps: Physics and Techniques of Charged Particle Field Confinement (Springer Series on Atomic, Optical, and Plasma Physics). Berlin: Springer. ISBN 3-540-22043-7. OCLC 231588573. 
• John Gillaspy (2001). Trapping Highly Charged Ions: Fundamentals and Applications. Commack, N.Y: Nova Science Publishers. ISBN 1-56072-725-X. OCLC 42009394. 
• Todd, John F. J.; March, Raymond E. (2005). Quadrupole Ion Trap Mass Spectrometry , 2nd Edition. New York: Wiley-Interscience. ISBN 0-471-48888-7. OCLC 56413336. 
• Todd, John F. J.; March, Raymond E. (1995). Practical aspects of ion trap mass spectrometry - Volume I: Fundamentals of Ion Trap Mass Spectrometry. Boca Raton: CRC Press. ISBN 0-8493-4452-2. OCLC 32346425. 
• Todd, John F. J.; March, Raymond E. (1995). Practical aspects of ion trap mass spectrometry: Ion Trap Instrumentation, Vol. 2. Boca Raton: CRC Press. ISBN 0-8493-8253-X. OCLC 32346425. 
• Todd, John F. J.; March, Raymond E. (1995). Practical aspects of ion trap mass spectrometry, Vol. 3. Boca Raton: CRC Press. ISBN 0-8493-8251-3. OCLC 32346425. 
• Hughes, Richard M.; March, Raymond E.; Todd, John F. J. (1989). Quadrupole storage mass spectrometry. New York: Wiley. ISBN 0-471-85794-7. OCLC 18290778. 
• K. Shah and H. Ramachandran, Analytic, nonlinearly exact solutions for an rf confined plasma, Phys. Plasmas 15, 062303 (2008), http://link.aip.org/link/?PHPAEN/15/062303/1
• Pradip K. Ghosh, Ion Traps, International Series of Monographs in Physics, Oxford University Press (1995), http://www.oup.com/us/catalog/general/subject/Physics/AtomicMolecularOpticalphysics/?view=usa&ci=9780198539957

Patents

• DE 944900  "Verfahren zur Trennung bzw. zum getrennten Nachweis von Ionen verschiedener spezifischer Ladung", W. Paul and H. Steinwedel, filed on December 24, 1953, priority December 23, 1953
• GB 773689  "Improved arrangements for separating or separately detecting charged particles of different specific charges", W. Paul, claims priority of a German application filed on December 23, 1953
• US 2939952  "Apparatus for separating charged particles of different specific charges", W. Paul and H. Steinwedel, claims priority of a German application filed on December 23, 1953

External links

• Nobel Prize in Physics 1989