Cylindrical coordinate system

A cylindrical coordinate system with origin O, polar axis A, and longitudinal axis L. The dot is the point with radial distance ρ = 4, angular coordinate φ = 130°, and height z = 4.

A cylindrical coordinate system is a three-dimensional coordinate system that specifies point positions by the distance from a chosen reference axis, the direction from the axis relative to a chosen reference direction, and the distance from a chosen reference plane perpendicular to the axis. The latter distance is given as a positive or negative number depending on which side of the reference plane faces the point.

The origin of the system is the point where all three coordinates can be given as zero. This is the intersection between the reference plane and the axis.

The axis is variously called the cylindrical or longitudinal axis, to differentiate it from the polar axis, which is the ray that lies in the reference plane, starting at the origin and pointing in the reference direction.

The distance from the axis may be called the radial distance or radius, while the angular coordinate is sometimes referred to as the angular position or as the azimuth. The radius and the azimuth are together called the polar coordinates, as they correspond to a two-dimensional polar coordinate system in the plane through the point, parallel to the reference plane. The third coordinate may be called the height or altitude (if the reference plane is considered horizontal), longitudinal position,^[1] or axial position.^[2]

Cylindrical coordinates are useful in connection with objects and phenomena that have some rotational symmetry about the longitudinal axis, such as water flow in a straight pipe with round cross-section, heat distribution in a metal cylinder, and so on.

Definition

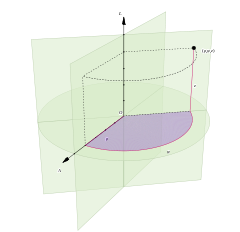
The three coordinates (ρ, φ, z) of a point P are defined as:

• The radial distance ρ is the Euclidean distance from the z axis to the point P.
• The azimuth φ is the angle between the reference direction on the chosen plane and the line from the origin to the projection of P on the plane.
• The height z is the signed distance from the chosen plane to the point P.

Unique cylindrical coordinates

As in polar coordinates, the same point with cylindrical coordinates (ρ, φ, z) has infinitely many equivalent coordinates, namely (ρ, φ ± n×360°, z) and (−ρ, φ ± (2n + 1)×180°, z), where n is any integer. Moreover, if the radius ρ is zero, the azimuth is arbitrary.

In situations where one needs a unique set of coordinates for each point, one may restrict the radius to be non-negative (ρ ≥ 0) and the azimuth φ to lie in a specific interval spanning 360°, such as (−180°,+180°] or [0,360°).

Conventions

The notation for cylindrical coordinates is not uniform. The ISO standard 31-11 recommends (ρ, φ, z), where ρ is the radial coordinate, φ the azimuth, and z the height. However, the radius is also often denoted r, the azimuth by θ or t, and the third coordinate by h or (if the cylindrical axis is considered horizontal) x, or any context-specific letter.

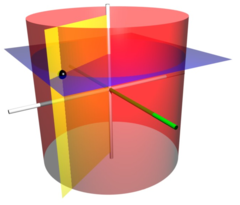The coordinate surfaces of the cylindrical coordinates (ρ, φ, z). The red cylinder shows the points with ρ=2, the blue plane shows the points with z=1, and the yellow half-plane shows the points with φ=−60°. The z-axis is vertical and the x-axis is highlighted in green. The three surfaces intersect at the point P with those coordinates (shown as a black sphere); the Cartesian coordinates of P are roughly (1.0, −1.732, 1.0).

Cylindrical Coordinate Surfaces. The three orthogonal components, ρ (green), φ (red), and z (blue), each increasing at a constant rate. The point is at the intersection between the three colored surfaces.

In concrete situations, and in many mathematical illustrations, a positive angular coordinate is measured counterclockwise as seen from any point with positive height.

Coordinate system conversions

The cylindrical coordinate system is one of many three-dimensional coordinate systems. The following formulae may be used to convert between them.

Cartesian coordinates

For the conversion between cylindrical and Cartesian coordinate systems, it is convenient to assume that the reference plane of the former is the Cartesian x–y plane (with equation z = 0) , and the cylindrical axis is the Cartesian z axis. Then the z coordinate is the same in both systems, and the correspondence between cylindrical (ρ,φ) and Cartesian (x,y) are the same as for polar coordinates, namely

x = ρcos φ

y = ρsin φ

in one direction, and

$\rho = \sqrt{x^{2}+y^{2}}$

$\varphi = \begin{cases} 0 & \mbox{if } x = 0 \mbox{ and } y = 0\\ \arcsin(\frac{y}{\rho}) & \mbox{if } x \geq 0 \\ -\arcsin(\frac{y}{\rho}) + \pi & \mbox{if } x < 0\\ \end{cases}$

in the other. The arcsin function is the inverse of the sine function, and is assumed to return an angle in the range [−π/2,+π/2] = [−90°,+90°]. These formulas yield an azimuth φ in the range [−90°,+270°]. For other formulas, see the polar coordinate article.

Many modern programming languages provide a function that will compute the correct azimuth φ, in the range (−π, π], given x and y, without the need to perform a case analysis as above. For example, this function is called by atan2(y,x) in the C programming language, and atan(y,x) in Common Lisp.

Spherical coordinates

Spherical coordinates (radius r, elevation or inclination θ, azimuth φ), may be converted into cylindrical coordinates by:

θ is elevation:		θ is inclination:
$\rho = r \cos \theta \,$		$\rho = r \sin \theta \,$
$\varphi = \varphi \,$		$\varphi = \varphi \,$
$z = r \sin \theta \,$		$z = r \cos \theta \,$

Cylindrical coordinates may be converted into spherical coordinates by:

θ is elevation:		θ is inclination:
$r=\sqrt{\rho^2+z^2}$		$r=\sqrt{\rho^2+z^2}$
${\theta}=\operatorname{arcsin}(z/r)$		${\theta}=\operatorname{arccos}(z/r)$
${\varphi}=\varphi \quad$		${\varphi}=\varphi \quad$

Line and volume elements

See multiple integral for details of volume integration in cylindrical coordinates, and Del in cylindrical and spherical coordinates for vector calculus formulae.

In many problems involving cylindrical polar coordinates, it is useful to know the line and volume elements; these are used in integration to solve problems involving paths and volumes.

The line element is

$\mathrm d\mathbf{r} = \mathrm d\rho\,\boldsymbol{\hat \rho} + \rho\,\mathrm d\varphi\,\boldsymbol{\hat\varphi} + \mathrm dz\,\mathbf{\hat z}.$

The volume element is

$\mathrm{d}V = \rho\,\mathrm{d}\rho\,\mathrm{d}\varphi\,\mathrm{d}z.$

The surface element in a surface of constant radius ρ (a vertical cylinder) is

$\mathrm{d}S_\rho= \rho\,\mathrm{d}\varphi\,\mathrm{d}z.$

The surface element in a surface of constant azimuth φ (a vertical half-plane) is

$\mathrm{d}S_\varphi= \mathrm{d}\rho\,\mathrm{d}z.$

The surface element in a surface of constant height z (a horizontal plane) is

$\mathrm{d}S_z= \rho\,\mathrm{d}\rho\,\mathrm{d}\varphi.$

The del operator in this system is written as

$\nabla = \boldsymbol{\hat \rho}\frac{\partial}{\partial \rho} + \boldsymbol{\hat \varphi}\frac{1}{\rho}\frac{\partial}{\partial \varphi} + \mathbf{\hat z}\frac{\partial}{\partial z},$

and the Laplace operator $\nabla^2$ is defined by

$\nabla^2 f = {1 \over \rho} {\partial \over \partial \rho} \left( \rho {\partial f \over \partial \rho} \right) + {1 \over \rho^2} {\partial^2 f \over \partial \varphi^2} + {\partial^2 f \over \partial z^2 }.$

Cylindrical harmonics

The solutions to the Laplace equation in a system with cylindrical symmetry are called cylindrical harmonics.

See also

• List of canonical coordinate transformations
• Vector fields in cylindrical and spherical coordinates
• Tricomplex number

References

1. ^ C. Krafft, A. S. Volokitin (2002), Resonant electron beam interaction with several lower hybrid waves. Physics of Plasmas, volume 9, issue 6, 2786–2797. DOI:10.1063/1.1465420 "[...]in cylindrical coordinates (r,θ,z) [...] and Z=v_bzt is the longitudinal position[...]".
2. ^ Alexander Groisman and Victor Steinberg (1997), Solitary Vortex Pairs in Viscoelastic Couette Flow. Physical Review Letters, volume 78, number 8, 1460–1463. DOI: 10.1103/PhysRevLett.78.1460 "[...]where r, θ, and z are cylindrical coordinates [...] as a function of axial position[...]"

Further reading

• Morse PM, Feshbach H (1953). Methods of Theoretical Physics, Part I. New York City: McGraw-Hill. pp. 6576–657. ISBN [[Special:BookSources/0-07-043316-X, LCCN 52-11515|0-07-043316-X, LCCN 52-11515]]. 
• Margenau H, Murphy GM (1956). The Mathematics of Physics and Chemistry. New York City: D. van Nostrand. p. 178. LCCN 55-10911. 
• Korn GA, Korn TM (1961). Mathematical Handbook for Scientists and Engineers. New York City: McGraw-Hill. pp. 174–175. LCCN 59-14456, ASIN B0000CKZX7. 
• Sauer R, Szabó I (1967). Mathematische Hilfsmittel des Ingenieurs. New York City: Springer-Verlag. p. 95. LCCN 67-25285. 
• Zwillinger D (1992). Handbook of Integration. Boston: Jones and Bartlett Publishers. p. 113. ISBN 0-86720-293-9. 
• Moon P, Spencer DE (1988). "Circular-Cylinder Coordinates (r, ψ, z)". Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions (corrected 2nd ed., 3rd print ed. ed.). New York City: Springer-Verlag. pp. 12–17 (Table 1.02). ISBN 978-0387184302. 

External links

• MathWorld description of cylindrical coordinates
• Cylindrical Coordinates Animations illustrating cylindrical coordinates by Frank Wattenberg