Paraboloidal coordinates

Paraboloidal coordinates are a three-dimensional orthogonal coordinate system (λ,μ,ν) that generalizes the two-dimensional parabolic coordinate system. Similar to the related ellipsoidal coordinates, the paraboloidal coordinate system has orthogonal quadratic coordinate surfaces that are not produced by rotating or projecting any two-dimensional orthogonal coordinate system.

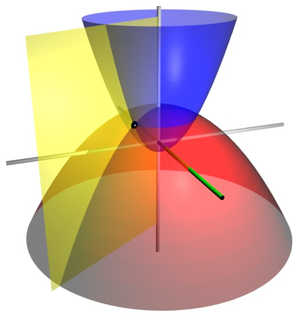Coordinate surfaces of the three-dimensional paraboloidal coordinates.

Basic formulae

The Cartesian coordinates (x,y,z) can be produced from the ellipsoidal coordinates (λ,μ,ν) by the equations

$x^{2} = \frac{\left( A - \lambda \right) \left( A - \mu \right) \left( A - \nu \right)}{B - A}$

$y^{2} = \frac{\left( B - \lambda \right) \left( B - \mu \right) \left( B - \nu \right)}{A - B}$

$z = \frac{1}{2} \left( A + B - \lambda - \mu -\nu \right)$

where the following limits apply to the coordinates

λ < B < μ < A < ν

Consequently, surfaces of constant λ are elliptic paraboloids

$\frac{x^{2}}{\lambda - A} + \frac{y^{2}}{\lambda - B} = 2z + \lambda$

and surfaces of constant ν are likewise

$\frac{x^{2}}{\nu - A} + \frac{y^{2}}{\nu - B} = 2z + \nu$

whereas surfaces of constant μ are hyperbolic paraboloids

$\frac{x^{2}}{\mu - A} + \frac{y^{2}}{\mu - B} = 2z + \mu$

Scale factors

The scale factors for the paraboloidal coordinates (λ,μ,ν) are

$h_{\lambda} = \frac{1}{2} \sqrt{\frac{\left( \mu - \lambda \right) \left( \nu - \lambda \right)}{ \left( A - \lambda \right) \left( B - \lambda \right)}}$

$h_{\mu} = \frac{1}{2} \sqrt{\frac{\left( \nu - \mu \right) \left( \lambda - \mu \right)}{ \left( A - \mu \right) \left( B - \mu \right)}}$

$h_{\nu} = \frac{1}{2} \sqrt{\frac{\left( \lambda - \nu \right) \left( \mu - \nu \right)}{ \left( A - \nu \right) \left( B - \nu \right)}}$

Hence, the infinitesimal volume element equals

$dV = \frac{\left( \mu - \lambda \right) \left( \nu - \lambda \right) \left( \nu - \mu\right)}{8\sqrt{\left( A - \lambda \right) \left( B - \lambda \right) \left( A - \mu \right) \left( \mu - B \right) \left( \nu - A \right) \left( \nu - B \right) }} \ d\lambda d\mu d\nu$

Differential operators such as $\nabla \cdot \mathbf{F}$ and $\nabla \times \mathbf{F}$ can be expressed in the coordinates (λ,μ,ν) by substituting the scale factors into the general formulae found in orthogonal coordinates.

References

Bibliography

• Morse PM, Feshbach H (1953). Methods of Theoretical Physics, Part I. New York: McGraw-Hill. p. 664. ISBN [[Special:BookSources/0-07-043316-X, LCCN 52-11515|0-07-043316-X, LCCN 52-11515]]. 
• Margenau H, Murphy GM (1956). The Mathematics of Physics and Chemistry. New York: D. van Nostrand. pp. 184–185. LCCN 55-10911. 
• Korn GA, Korn TM (1961). Mathematical Handbook for Scientists and Engineers. New York: McGraw-Hill. p. 180. LCCN 59-14456, ASIN B0000CKZX7. 
• Arfken G (1970). Mathematical Methods for Physicists (2nd ed. ed.). Orlando, FL: Academic Press. pp. 119–120. 
• Sauer R, Szabó I (1967). Mathematische Hilfsmittel des Ingenieurs. New York: Springer Verlag. p. 98. LCCN 67-25285. 
• Zwillinger D (1992). Handbook of Integration. Boston, MA: Jones and Bartlett. p. 114. ISBN 0-86720-293-9.  Same as Morse & Feshbach (1953), substituting u_k for ξ_k.
• Moon P, Spencer DE (1988). "Paraboloidal Coordinates (μ, ν, λ)". Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions (corrected 2nd ed., 3rd print ed. ed.). New York: Springer-Verlag. pp. 44–48 (Table 1.11). ISBN 978-0387184302. 

External links

• MathWorld description of confocal paraboloidal coordinates