Conical coordinates

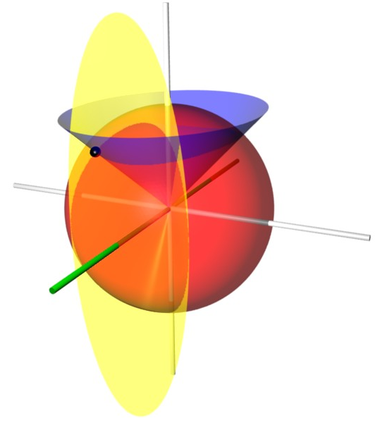Coordinate surfaces of the conical coordinates. The constants b and c were chosen as 1 and 2, respectively. The red sphere represents r=2, the blue elliptic cone aligned with the vertical z-axis represents μ=cosh(1) and the yellow elliptic cone aligned with the (green) x-axis corresponds to ν² = 2/3. The three surfaces intersect at the point P (shown as a black sphere) with Cartesian coordinates roughly (1.26, -0.78, 1.34). The elliptic cones intersect the sphere in taco-shaped curves.

Conical coordinates are a three-dimensional orthogonal coordinate system consisting of concentric spheres (described by their radius r) and by two families of perpendicular cones, aligned along the z- and x-axes, respectively.

Basic definitions

The conical coordinates (r,μ,ν) are defined by

$x = \frac{r\mu\nu}{bc}$

$y = \frac{r}{b} \sqrt{\frac{\left( \mu^{2} - b^{2} \right) \left( \nu^{2} - b^{2} \right)}{\left( b^{2} - c^{2} \right)} }$

$z = \frac{r}{c} \sqrt{\frac{\left( \mu^{2} - c^{2} \right) \left( \nu^{2} - c^{2} \right)}{\left( c^{2} - b^{2} \right)} }$

with the following limitations on the coordinates

ν² < c² < μ² < b²

Surfaces of constant r are spheres of that radius centered on the origin

x² + y² + z² = r²

whereas surfaces of constant μ and ν are mutually perpendicular cones

$\frac{x^{2}}{\mu^{2}} + \frac{y^{2}}{\mu^{2} - b^{2}} + \frac{z^{2}}{\mu^{2} - c^{2}} = 0$

$\frac{x^{2}}{\nu^{2}} + \frac{y^{2}}{\nu^{2} - b^{2}} + \frac{z^{2}}{\nu^{2} - c^{2}} = 0$

In this coordinate system, both Laplace's equation and the Helmholtz equation are separable.

Scale factors

The scale factor for the radius r is one (h_r = 1), as in spherical coordinates. The scale factors for the two conical coordinates are

$h_{\mu} = r \sqrt{\frac{\mu^{2} - \nu^{2}}{\left( b^{2} - \mu^{2} \right) \left( \mu^{2} - c^{2} \right)}}$

$h_{\nu} = r \sqrt{\frac{\mu^{2} - \nu^{2}}{\left( b^{2} - \nu^{2} \right) \left( c^{2} - \nu^{2} \right)}}$

References

Bibliography

• Morse PM, Feshbach H (1953). Methods of Theoretical Physics, Part I. New York: McGraw-Hill. p. 659. ISBN [[Special:BookSources/0-07-043316-X, LCCN 52-11515|0-07-043316-X, LCCN 52-11515]]. 
• Margenau H, Murphy GM (1956). The Mathematics of Physics and Chemistry. New York: D. van Nostrand. pp. 183–184. LCCN 55-10911. 
• Korn GA, Korn TM (1961). Mathematical Handbook for Scientists and Engineers. New York: McGraw-Hill. p. 179. LCCN 59-14456, ASIN B0000CKZX7. 
• Sauer R, Szabó I (1967). Mathematische Hilfsmittel des Ingenieurs. New York: Springer Verlag. pp. 991–100. LCCN 67-25285. 
• Arfken G (1970). Mathematical Methods for Physicists (2nd ed. ed.). Orlando, FL: Academic Press. pp. 118–119. ASIN B000MBRNX4. 
• Moon P, Spencer DE (1988). "Conical Coordinates (r, θ, λ)". Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions (corrected 2nd ed., 3rd print ed. ed.). New York: Springer-Verlag. pp. 37–40 (Table 1.09). ISBN 978-0387184302. 

External links

• MathWorld description of conical coordinates