- Conical intersection
-
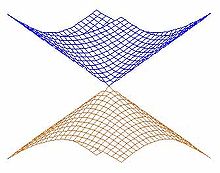
In quantum chemistry, a conical intersection of two potential energy surfaces of the same spatial and spin symmetries is the set of molecular geometry points where the two potential energy surfaces are degenerate (intersect). Conical intersections are ubiquitous in both trivial and non-trivial chemical systems.In a two coordinate system, this can occur at one molecular geometry. If the potential energy surfaces are plotted as functions of the two coordinates, they form a cone centered at the degeneracy point. This is shown in the picture on the right, where the upper and lower potential energy surfaces are plotted in different colors. The name conical intersection comes from this observation.
In a system with n coordinates, degenerate points lie in what is called the intersection space, or seam. The dimensionality of the seam is n-2. For a conical intersection, the remaining two dimensions that lift the energetic degeneracy of the system are known as the branching space.
The conical intersections are also called molecular funnels or diabolic points. This comes from the very important role they play in non-radiative de-excitation transitions from excited electronic states to the ground electronic state of molecules. For example, the stability of DNA with respect to the UV irradiation is due to such conical intersection. The molecular wave packet excited to some electronic excited state by the UV photon follows the slope of the potential energy surface and reaches the conical intersection from above. At this point the very large vibronic coupling induces a non-radiative transition (surface-hopping) which leads the molecule back to its electronic ground state.
A well-written introduction to the topic of conical intersections in chemistry is Diabolical Conical Intersections, David Yarkony, Rev. Mod. Phys. 68, 985-1013 (1996).
A clear authoritative book on the intricate mathematical aspects of conical intersections can be found in Beyond Born-Oppenheimer: Electronic Nonadiabatic Coupling Terms and Conical Intersections by Michael Baer (Wiley-Interscience, 2006).
External links
Categories:
Wikimedia Foundation. 2010.