Cylinder (geometry)

A right circular cylinder

A cylinder is one of the most basic curvilinear geometric shapes, the surface formed by the points at a fixed distance from a given line segment, the axis of the cylinder. The solid enclosed by this surface and by two planes perpendicular to the axis is also called a cylinder. The surface area and the volume of a cylinder have been known since deep antiquity.

In differential geometry, a cylinder is defined more broadly as any ruled surface spanned by a one-parameter family of parallel lines. A cylinder whose cross section is an ellipse, parabola, or hyperbola is called an elliptic cylinder, parabolic cylinder, or hyperbolic cylinder respectively.

Common use

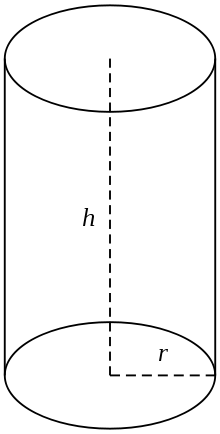
In common use a cylinder is taken to mean a finite section of a right circular cylinder, i.e., the cylinder with the generating lines perpendicular to the bases, with its ends closed to form two circular surfaces, as in the figure (right). If the cylinder has a radius r and length (height) h, then its volume is given by

V = πr²h

and its surface area is:

• the area of the top (πr²) +
• the area of the bottom (πr²) +
• the area of the side (2πrh).

Therefore without the top or bottom (lateral area), the surface area is:

A = 2πrh.

With the top and bottom, the surface area is:

A = 2πr² + 2πrh = 2πr(r + h).

For a given volume, the cylinder with the smallest surface area has h = 2r. For a given surface area, the cylinder with the largest volume has h = 2r, i.e. the cylinder fits in a cube (height = diameter).

Volume

Having a right circular cylinder with a height h units and a base of radius r units with the coordinate axes chosen so that the origin is at the center of one base and the height is measured along the positive x-axis. A plane section at a distance of x units from the origin has an area of A(x) square units where

A(x) = πr²

or

A(y) = πr²

An element of volume, is a right cylinder of base area Aw_i square units and a thickness of Δ_ix units. Thus if V cubic units is the volume of the right circular cylinder, by Riemann sums,

$\mathrm{Volume \; of \; cylinder}=\lim_{||\Delta \to 0 ||} \sum_{i=1}^n A(w_i) \Delta_i x$

$=\int_{0}^{h} A(y) \, dy$

$=\int_{0}^{h} \pi r^2 \, dy$

$=\pi\,r^2\,h\,$

Using cylindrical coordinates, the volume can be calculated by integration over

$=\int_{0}^{h} \int_{0}^{2\pi} \int_{0}^{r} s \,\, ds \, d\phi \, dz$

$=\pi\,r^2\,h\,$

Cylindric section

Cylindric sections are the intersections of cylinders with planes. For a right circular cylinder, there are four possibilities. A plane tangent to the cylinder, meets the cylinder in a single straight line. Moved while parallel to itself, the plane either does not intersect the cylinder or intersects it in two parallel lines. All other planes intersect the cylinder in an ellipse or, when they are perpendicular to the axis of the cylinder, in a circle.^[1]

Other types of cylinders

An elliptic cylinder

An elliptic cylinder, or cylindroid, is a quadric surface, with the following equation in Cartesian coordinates:

$\left(\frac{x}{a}\right)^2+ \left(\frac{y}{b}\right)^2 = 1$

This equation is for an elliptic cylinder, a generalization of the ordinary, circular cylinder (a = b). Even more general is the generalized cylinder: the cross-section can be any curve.

The cylinder is a degenerate quadric because at least one of the coordinates (in this case z) does not appear in the equation.

An oblique cylinder has the top and bottom surfaces displaced from one another.

There are other more unusual types of cylinders. These are the imaginary elliptic cylinders:

$\left(\frac{x}{a}\right)^2 + \left(\frac{y}{b}\right)^2 = -1$

the hyperbolic cylinder:

$\left(\frac{x}{a}\right)^2 - \left(\frac{y}{b}\right)^2 = 1$

and the parabolic cylinder:

${x}^2+2a{y}=0 \,$

About an arbitrary axis

To describe the cylindrical surface surrounding an arbitrary axis

$v = (\alpha, \beta, \gamma) \,$

We make use of spherical coordinates:

$\rho^2=\alpha^2+\beta^2+\gamma^2\,$

$\theta=arctan\left(\frac{\beta}{\alpha}\right)$

$\phi=arcsin\left(\frac{\gamma}{\rho}\right)$

These variables can be used to define A and B, the orthogonal vectors that form the basis for the cylinder:

A = − xsin(θ) + ycos(θ)cos(ϕ) + zcos(θ)sin(ϕ)

B = − ysin(ϕ) + zcos(ϕ)

With these defined, we may use the familiar formula for a cylinder:

$A^2 + B^2 = R^2 \,$

where R is the radius of the cylinder. These results are usually derived using rotation matrices.

Projective geometry

In projective geometry, a cylinder is simply a cone whose apex is at infinity, which corresponds visually to a cylinder in perspective appearing to be a cone towards the sky.

In projective geometry, a cylinder is simply a cone whose apex is at infinity.

This is useful in the definition of degenerate conics, which require considering the cylindrical conics.

See also

• Steinmetz solid, the intersection of two or three perpendicular cylinders
• Prism (geometry)

References

1. ^ "MathWorld: Cylindric section". http://mathworld.wolfram.com/CylindricSection.html. 

External links

• Surface area of a cylinder at MATHguide
• Volume of a cylinder at MATHguide
• Spinning Cylinder at Math Is Fun
• Volume of a cylinder Interactive animation at Math Open Reference
• Cut a Cylinder Interactive demonstrations of the intersection of a plane and a cylinder