Mathieu function

In mathematics, the Mathieu functions are certain special functions useful for treating a variety of problems in applied mathematics, including

• vibrating elliptical drumheads,
• quadrupoles mass filters and quadrupole ion traps for mass spectrometry
• wave motion in periodic media, such as ultracold atoms in an optical lattice
• the phenomenon of parametric resonance in forced oscillators,
• exact plane wave solutions in general relativity,
• the Stark effect for a rotating electric dipole,
• in general, the solution of differential equations that are separable in elliptic cylindrical coordinates.

They were introduced by Émile Léonard Mathieu (1868) in the context of the first problem.

Mathieu equation

The canonical form for Mathieu's differential equation is

$\frac{d^2y}{dx^2}+[a-2q\cos (2x) ]y=0.$

Closely related is Mathieu's modified differential equation

$\frac{d^2y}{du^2}-[a-2q\cosh (2u) ]y=0$

which follows on substitution u = ix.

The substitution t = cos(x) transforms Mathieu's equation to the algebraic form

$(1-t^2)\frac{d^2y}{dt^2} - t\, \frac{d y}{dt} + (a + 2q (1- 2t^2)) \, y=0.$

This has two regular singularities at t = − 1,1 and one irregular singularity at infinity, which implies that in general (unlike many other special functions), the solutions of Mathieu's equation cannot be expressed in terms of hypergeometric functions.

Mathieu's differential equations arise as models in many contexts, including the stability of railroad rails as trains drive over them, seasonally forced population dynamics, the four-dimensional wave equation, and the Floquet theory of the stability of limit cycles.

Floquet solution

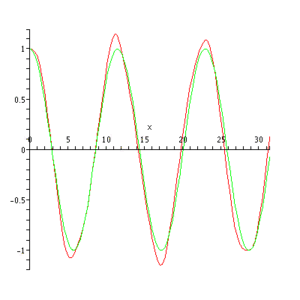
According to Floquet's theorem (or Bloch's theorem), for fixed values of a,q, Mathieu's equation admits a complex valued solution of form

$F(a,q,x) = \exp(i \mu \,x) \, P(a,q,x)$

where μ is a complex number, the Mathieu exponent, and P is a complex valued function which is periodic in x with period π. However, P is in general not sinusoidal. In the example plotted below, $a=1, \, q=\frac{1}{5}, \, \mu \approx 1 + 0.0995 i$ (real part, red; imaginary part; green):

Mathieu sine and cosine

For fixed a,q, the Mathieu cosine C(a,q,x) is a function of x defined as the unique solution of the Mathieu equation which

1. takes the value C(a,q,0) = 1,
2. is an even function, hence $C^\prime(a,q,0)=0$.

Similarly, the Mathieu sine S(a,q,x) is the unique solution which

1. takes the value $S^\prime(a,q,0)=1$,
2. is an odd function, hence S(a,q,0) = 0.

These are real-valued functions which are closely related to the Floquet solution:

$C(a,q,x) = \frac{F(a,q,x) + F(a,q,-x)}{2 F(a,q,0)}$

$S(a,q,x) = \frac{F(a,q,x) - F(a,q,-x)}{2 F^\prime(a,q,0)}.$

The general solution to the Mathieu equation (for fixed a,q) is a linear combination of the Mathieu cosine and Mathieu sine functions.

A noteworthy special case is

$C(a,0,x) = \cos(\sqrt{a} x), \; S(a,0,x) = \frac{\sin(\sqrt{a} x)}{\sqrt{a}}.$

In general, the Mathieu sine and cosine are aperiodic. Nonetheless, for small values of q, we have approximately

$C(a,q,x) \approx \cos(\sqrt{a} x), \; \; S(a,q,x) \approx \frac{\sin (\sqrt{a} x)}{\sqrt{a}}.$

For example:

Red: C(0.3,0.1,x).

Red: C'(0.3,0.1,x).

Periodic solutions

Given q, for countably many special values of a, called characteristic values, the Mathieu equation admits solutions which are periodic with period 2π. The characteristic values of the Mathieu cosine, sine functions respectively are written $a_n(q), \, b_n(q)$, where n is a natural number. The periodic special cases of the Mathieu cosine and sine functions are often written $CE(n,q,x), \, SE(n,q,x)$ respectively, although they are traditionally given a different normalization (namely, that their L² norm equal π). Therefore, for positive q, we have

$C \left( a_n(q),q,x \right) = \frac{CE(n,q,x)}{CE(n,q,0)}$

$S \left( b_n(q),q,x \right) = \frac{SE(n,q,x)}{SE^\prime(n,q,0)}.$

Here are the first few periodic Mathieu cosine functions for q = 1:

Note that, for example, CE(1,1,x) (green) resembles a cosine function, but with flatter hills and shallower valleys.

See also

• Monochromatic electromagnetic plane wave, an example of an important exact plane wave solution to the Einstein field equation in general relativity which is expressed using Mathieu cosine functions.
• Inverted pendulum
• Lamé function

References

• Mathieu, E. (1868). "Mémoire sur Le Mouvement Vibratoire d’une Membrane de forme Elliptique". Journal des Mathématiques Pures et Appliquées: 137–203. http://visualiseur.bnf.fr/ConsulterElementNum?O=NUMM-16412&Deb=145&Fin=211&E=PDF. 
• Gertrude Blanch, "Chapter 20. Mathieu Functions", in Milton Abramowitz and Irene A. Stegun, eds., Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables (Dover: New York, 1972)
• McLachlan, N. W. (1962 (reprint of 1947 ed.)). Theory and application of Mathieu functions. New York: Dover. LCCN 64016333. 
• Wolf, G. (2010), "Mathieu Functions and Hill’s Equation", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F. et al., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0521192255, MR2723248, http://dlmf.nist.gov/28 

External links

• Timothy Jones, Mathieu's Equations and the Ideal rf-Paul Trap (2006)
• Weisstein, Eric W., "Mathieu function" from MathWorld.
• Mathieu equation, EqWorld
• List of equations and identities for Mathieu Functions functions.wolfram.com
• NIST Digital Library of Mathematical Functions: Mathieu Functions and Hill's Equation