Spring (device)

Helical or coil springs designed for tension

Compression springs store energy when compressed

The English longbow – a simple but very powerful spring made of yew, measuring 2 m (6 ft 6 in) long, with a 470 N (105 lbf) draw force

A machined spring incorporates several features into one piece of bar stock

Military boobytrap firing device from USSR (normally connected to a tripwire) showing spring-loaded firing pin

A spring is an elastic object used to store mechanical energy.

When a spring is compressed or stretched, the force it exerts is proportional to its change in length. The rate or spring constant of a spring is the change in the force it exerts, divided by the change in deflection of the spring. That is, it is the gradient of the force versus deflection curve. An extension or compression spring has units of force divided by distance, for example lbf/in or N/m. Torsion springs have units of force multiplied by distance divided by angle, such as N·m/rad or ft·lbf/degree. The inverse of spring rate is compliance, that is: if a spring has a rate of 10 N/mm, it has a compliance of 0.1 mm/N. The stiffness (or rate) of springs in parallel is additive, as is the compliance of springs in series.

History

Simple non-coiled springs were used throughout human history e.g., the bow (and arrow). In the Bronze Age more sophisticated spring devices were used, as shown by the spread of tweezers in many cultures. Ctesibius of Alexandria developed a method for making bronze with spring-like characteristics by producing an alloy of bronze with an increased proportion of tin, and then hardening it by hammering after it is cast.

Coiled springs appeared early in the 15th century,^[1] in door locks.^[2] The first spring powered-clocks appeared in that century^[2][3][4] and evolved into the first large watches by the 16th century.

In 1676 British physicist Robert Hooke discovered the principle behind springs' action, that the force it exerts is proportional to its extension, now called Hooke's law.

Materials

Theoretically, any material can be used to construct a spring, so long as the material has the required combination of rigidity and elasticity: technically, a wooden bow is a form of spring. Springs are usually made out of spring steel. Small springs can be wound from pre-hardened stock, while larger ones are made from annealed steel and hardened after fabrication.

Depending on the design, installation and operating environmental conditions such as corrosive surroundings, temperature variations, shock loading, fatigue life desired, and a number of other conditions, it is necessary to use different types of spring materials.^[5] These materials can be placed into groups such as high-carbon steels, alloy steels, stainless steels, copper-base alloys, nickel-base alloys, and several other groups having special qualities. Some non-ferrous metals are also used including phosphor bronze and titanium for parts requiring corrosion resistance and beryllium copper for springs carrying electrical current (because of its low electrical resistance).

Most spring materials are covered by ASTM standards and by SAE, AISI and federal specifications. Some manufacturing companies and wire mills also have their own specifications.

Types

A spiral torsion spring, or hairspring, in an alarm clock.

A volute spring. Under compression the coils slide over each other, so affording longer travel.

Vertical volute springs of Stuart tank

Tension springs in a folded line reverberation device.

A torsion bar twisted under load

Leaf spring on a truck

Springs can be classified depending on how the load force is applied to them:

• Tension/Extension spring – the spring is designed to operate with a tension load, so the spring stretches as the load is applied to it.
• Compression spring – is designed to operate with a compression load, so the spring gets shorter as the load is applied to it.
• Torsion spring – unlike the above types in which the load is an axial force, the load applied to a torsion spring is a torque or twisting force, and the end of the spring rotates through an angle as the load is applied.

They can also be classified based on their shape:

• Coil spring – this type is made of a coil or helix of wire
• Flat spring – this type is made of a flat or conical shaped piece of metal.
• Machined spring - this type of spring is manufactured by machining bar stock with a lathe and/or milling operation rather than coiling wire. Since it is machined, the spring may incorporate features in addition to the elastic element. Machined springs can be made in the typical load cases of compression/extension, torsion, etc.

The most common types of spring are:

• Cantilever spring – a spring which is fixed only at one end.
• Coil spring or helical spring – a spring (made by winding a wire around a cylinder) and the conical spring – these are types of torsion spring, because the wire itself is twisted when the spring is compressed or stretched. These are in turn of two types:
  • Compression springs are designed to become shorter when loaded. Their turns (loops) are not touching in the unloaded position, and they need no attachment points.
    • A volute spring is a compression spring in the form of a cone, designed so that under compression the coils are not forced against each other, thus permitting longer travel.
  • Tension or extension springs are designed to become longer under load. Their turns (loops) are normally touching in the unloaded position, and they have a hook, eye or some other means of attachment at each end.
• Hairspring or balance spring – a delicate spiral torsion spring used in watches, galvanometers, and places where electricity must be carried to partially-rotating devices such as steering wheels without hindering the rotation.
• Leaf spring – a flat spring used in vehicle suspensions, electrical switches, and bows.
• V-spring – used in antique firearm mechanisms such as the wheellock, flintlock and percussion cap locks.

Other types include:

• Belleville washer or Belleville spring – a disc shaped spring commonly used to apply tension to a bolt (and also in the initiation mechanism of pressure-activated landmines).
• Constant-force spring — a tightly rolled ribbon that exerts a nearly constant force as it is unrolled.
• Gas spring – a volume of gas which is compressed.
• Ideal Spring – the notional spring used in physics: it has no weight, mass, or damping losses.
• Mainspring – a spiral ribbon shaped spring used as a power source in watches, clocks, music boxes, windup toys, and mechanically powered flashlights
• Negator spring – a thin metal band slightly concave in cross-section. When coiled it adopts a flat cross-section but when unrolled it returns to its former curve, thus producing a constant force throughout the displacement and negating any tendency to re-wind. The commonest application is the retracting steel tape rule.^[6]
• Progressive rate coil springs – A coil spring with a variable rate, usually achieved by having unequal pitch so that as the spring is compressed one or more coils rests against its neighbour.
• Rubber band – a tension spring where energy is stored by stretching the material.
• Spring washer – used to apply a constant tensile force along the axis of a fastener.
• Torsion spring – any spring designed to be twisted rather than compressed or extended. Used in torsion bar vehicle suspension systems.
• Wave spring – a thin spring-washer into which waves have been pressed.^[7]

Special springs

In addition to traditional helical springs there are many types of springs that are used occasionally.Some of them are as:

1. Flat springs
2. Leaf springs
3. Spiral springs
4. Power or motor springs

Flat springs

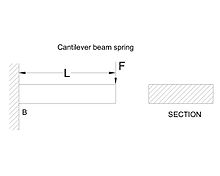
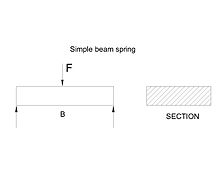
Flat springs are used to keep within space conditions in various products such as switches and relays. Flat springs may be in the form of cantilever beam,or in the form of simple beams.Figures shows both flat cantilever spring and simple beam spring.

Add caption here

Add caption here

In the cantilever flat spring maximum stress occurs at the support point B as shown in figure.Since the bending stress occurs at the for a constant cross section diminishes from support point B to point of application force,i.e,F,the section of beam may be in such a manner that the bending stress on each section is the same.the resulting beam is called as beam of uniform strength. Simple beams have bit different characteristics than cantilever type but they can be calculated same as those of cantilever type. The nominal stresses in this flat springs can be calculated using bending moment formula,provided that the deflection in spring is not too large.

Leaf Springs

Leaf springs ^[8] are widely used in transport sector for vehicles such as cars, trucks, buses etc. Leaf spring is nothing but an assembly of various flat springs. So we can determine the properties of the leaf apring form the individual characteristics of flat spring that is used in assembly. Figure shows leaf spring and its parts.

Add caption here

It is necessary to modify the springs of uniform strength in order to make them practicable on commercial scale. The simple beam of uniform strength becomes semi-elliptical leaf spring and thus when assembled with same pieces gives improved performance and strength. Various parts of leaf springs are:

1. Camber: distance between horizontal line and maximum deflected part of leaf.
2. Spring eye: It is rounded circular edge of longest leaf to hold the spring.
3. Center Bolt: The bolt at the central position to hold all the leafs together.
4. Rebound clips: These are accessory clips at the periphery of leafs to hold the leafs.

Automotive Leaf Spring

For automotive leaf springs not all the leafs are of same thickness. Also they don't even have same center of curvature in loaded positions as well as with different radius of curvature. Rebound is the most problem of concern in automotive leaf springs. Because an unchecked rebound after a bump may bend the leaves until the stress is dangerously high. Thus, shock absorbers act not only to improve the ride but also they prevent spring failure.

Spiral springs

Spiral spring configurations perform the twist function.They are used in watches,toys and in the components where twist function is to be performed.Figure shows 3d view of spiral spring.

Add caption here

These are general used as brush springs in DC motors, anti-backslash springs, Alternators, Drill presses, Vertical mill, Counter balance springs etc. These are generally made of rectangular section material, flat strip, with round edges or normal slit edges with equal or increasing space between coils.For first 3600, torque delivered per revolution is linear. Therefore, these are generally used for less than 3600 rotational applications. If the these springs are totated more than one turn the coils will touch each other causing friction leading to erratic loads. They generally have a lug across the I.D. of the spring, which engages a slot in the shaft, over which it works. The I.D. can be made with holes to engage an arbor protrusion or can be made in a special shape to fit over a similar shaped shaft. The outside end can be formed as per customer's requirement.

Power or motor springs

Power or motor springs are generally used to save the potential energy and deliver it on requirement as kinetic energy,such as spring in clock.Depending on requirements, where there is a requirement to obtain several turns from a torsion spring, motor springs can be used instead.

Add caption here

Motor springs are locked to a shaft with a catch, and to a pin or housing edge. This design can give 10-20 turns of spring force. If you need more torque than what one motor spring can perform, just use several motor springs next to each other. The motor springs are often represented in the electric power industry in for example distribution plants, usually manufactured in stainless steel.

Physics

Two springs attached to a wall and a mass. In a situation like this, the two springs can be replaced by one with a spring constant of k_eq=k₁+k₂.

Hooke's law

Main article: Hooke's law

As long as they are not stretched or compressed beyond their elastic limit, most springs obey Hooke's law, which states that the force with which the spring pushes back is linearly proportional to the distance from its equilibrium length:

$F=-kx, \$

where

x is the displacement vector – the distance and direction in which the spring is deformed

F is the resulting force vector – the magnitude and direction of the restoring force the spring exerts

k is the rate, spring constant or force constant of the spring, a constant that depends on the spring's material and construction.

Coil springs and other common springs typically obey Hooke's law. There are useful springs that don't: springs based on beam bending can for example produce forces that vary nonlinearly with displacement.

Simple harmonic motion

Main article: Harmonic oscillator

Since force is equal to mass, m, times acceleration, a, the force equation for a spring obeying Hooke's law looks like:

$F = m a \quad \Rightarrow \quad -k x = m a. \,$

The displacement, x, as a function of time. The amount of time that passes between peaks is called the period.

The mass of the spring is assumed small in comparison to the mass of the attached mass and is ignored. Since acceleration is simply the second derivative of x with respect to time,

$- k x = m \frac{d^2 x}{dt^2}. \,$

This is a second order linear differential equation for the displacement x as a function of time. Rearranging:

$\frac{d^2 x}{dt^2} + \frac{k}{m} x = 0, \,$

the solution of which is the sum of a sine and cosine:

$x(t) = A \sin \left( t \sqrt{\frac{k}{m}} \right) + B \cos \left(t \sqrt{\frac{k}{m}} \right). \,$

A and B are arbitrary constants that may be found by considering the initial displacement and velocity of the mass. The graph of this function with B = 0 (zero initial position with some positive initial velocity) is displayed in the image on the right.

Theory

In classical physics, a spring can be seen as a device that stores potential energy, specifically elastic potential energy, by straining the bonds between the atoms of an elastic material.

Hooke's law of elasticity states that the extension of an elastic rod (its distended length minus its relaxed length) is linearly proportional to its tension, the force used to stretch it. Similarly, the contraction (negative extension) is proportional to the compression (negative tension).

This law actually holds only approximately, and only when the deformation (extension or contraction) is small compared to the rod's overall length. For deformations beyond the elastic limit, atomic bonds get broken or rearranged, and a spring may snap, buckle, or permanently deform. Many materials have no clearly defined elastic limit, and Hooke's law can not be meaningfully applied to these materials. Moreover, for the superelastic materials, the linear relationship between force and displacement is appropriate only in the low-strain region.

Hooke's law is a mathematical consequence of the fact that the potential energy of the rod is a minimum when it has its relaxed length. Any smooth function of one variable approximates a quadratic function when examined near enough to its minimum point; and therefore the force — which is the derivative of energy with respect to displacement — will approximate a linear function.

Force of fully compressed spring

$F_{max} = \frac{E d^4 (L-n d)}{16 (1+\nu) (D-d)^3 n} \$

where

E – Young's modulus

d – spring wire diameter

L – free length of spring

n – number of active windings

ν – Poisson ratio

D – spring outer diameter

Stress in round-wire helical springs

For an axially loaded spring with force F,having mean diameter of coil D_m,

$T = \frac{F D_m}{2}\$ (1)

This same torsional moment exists in all sections of the loaded spring. For the loaded spring the torsional resisting moment can be given by

$= \frac{s_s \pi D_w^3}{16}\$ (2)

Equating equations 1 and 2 we get,

$s_s = \frac{8 F D_m}{\pi D_w^3}\$ (3)

Where, D_w - diameter of the cross section of wire
s_s - stress that underrates resultant of torsional stress, direct shear across any section,bending stress. Several investigators have made more precise analyses, considering one or all of the above additional factors, one of the most practicable being analysis by Wahl.^{[citation needed]} Wahl obtained factor K_a to be used with equation (3) as,

$s_s = K_a \frac{8 F D_m}{\pi D_w^3}\$.

This equation can be used to compute stress in closely coiled string; And K_a can be found as,

$K_a = \frac{4 C - 1}{4 C - 4}\ + \frac{0.615}{C}\$,

where, $C = \frac{D_m}{D_w}\$ and is called as 'spring index'.

Zero-length springs

"Zero-length spring" is a term for a specially-designed coil spring that would exert zero force if it had zero length. That is, in a line graph of the spring's force versus its length, the line passes through the origin. Obviously a coil spring cannot contract to zero length because at some point the coils will touch each other and the spring will not be able to shorten any more. Zero length springs are made by manufacturing a coil spring with built-in tension, so if it could contract further, the equilibrium point of the spring, the point at which its restoring force is zero, occurs at a length of zero. In practice, zero length springs are made by combining a "negative length" spring, made with even more tension so its equilibrium point would be at a "negative" length, with a piece of inelastic material of the proper length so the zero force point would occur at zero length.

A spring with zero length can be attached to a mass on a hinged boom in such a way that the force on the mass is almost exactly balanced by the vertical component of the force from the spring, whatever the position of the boom. This creates a pendulum with very long period. Long-period pendulums enable seismometers to sense the slowest waves from earthquakes. The LaCoste suspension^[9] with zero-length springs is also used in gravimeters because it is very sensitive to changes in gravity. Springs for closing doors are often made to have roughly zero length so that they will exert force even when the door is almost closed, so it will close firmly.

Proficient Analysis of Springs

Spring rate: refers to the amount of weight needed to compress a spring an inch Things whch affect spring rate :
1. Wire diameter - This affects rate since greater diameter wire is stronger than lesser diameter wire. So, when wire diameter is increased, spring rate increases.
2. Mean diameter of spring - Mean diameter is the overall outside diameter of the spring less one wire diameter. When mean diameter increases, the spring rate decreases.
3. Active coils - Determination of the number of active coils varies according to spring design.

Dynamics of coil springs

There are basically three different spring designs presently used in race cars. They are:

1. Closed and ground on both ends (Coil-overs and rear conventional springs are this type).
2. Closed both ends but ground one end only (Conventional front springs are normally this type).
3. Closed and ground on one end and open on the other end (Similar to a conventional spring that has been cut).

The 3 spring types are used in different situations and provide different effects to rate. Since the designs are so varied, it only follows that the dynamics of each design are also varied.

Uses

Springs are used in many purposes. And also one spring can be used for various purposes simultaneously. There are some of functional purposes.

1. It can be used to store energy for a part of functioning cycles.
2. Also it can be used to couple two different components i.e. to force, to engage, to maintain contact with, to remain clear of some other components.
3. Springs, as an electrical device, are useful to maintain continuation in electrical circuit.
4. To counterbalance the weight or thrust, springs are used.
5. For a component, to regain its original position, springs can be used.
6. To decrease the shock or vibrations by observing the motion of moving weight.

• Balance springs mechanical timepieces
• Buckling spring keyboards
• In CD players
• Inside a pen
• Mattress
• Pogo Stick
• Slinky
• Trampoline
• Vehicle suspension
• Whammy bar

Failure analysis

Causes of failure

A number of factors need to be taken into consideration while carrying out spring failure analysis.^[10] These factors may be listed as follows.

1) Fatigue

The large majority of true fatigue failures are due to high stresses caused due to large deflections and high forces. A true fatigue failure of any spring always initiates from some miniscule imperfection on the inside diameter of the spring and then proceeds outward at a 45° angle to the outside diameter.this happens due to the stress is always highest on the inside diameter of the coils and least on the outside diameter.

2) Hydrogen embrittlement

When springs made from high-carbon or alloy spring steels are cleaned by dipping or are electroplated , they pick up atomic hydrogen along the grain boundaries. This inclusion retards the slipping or even natural movement of the grains as deflection takes place. An easy and sure test to determine if the plated spring broke due to hydrogen embrittlement is to hold the broken spring, or a coil,in a vise and grip the extended portion with sure-grip pliers and bend the coil. Usually a 45° to 90° bend will cause it to break in a very brittle manner. A broken coil easily be broken again into two or three parts.

3) Sharp bends

Sharp bends cause the bunching up of the grains on the inside of a bend and pull the grains apart on the outside of the bend. The distortion of grains not only weakens the bending area but also traps high residual stresses that make it especially susceptible to hydrogen embrittlement when the spring are plated. Holes or notches in flat springs also induce a concentration of stress that can cause cracks to occur.

4) Shock

Compression springs subjected to shock loading, high dynamic forces, or rapid loading usually break on the second or the third active coil, because the first two or three active coils receive the load first and cannot transmit it quickly enough to the other coils. The first two or three active coils absorb most of the impact and may be compressed much farther than the remaining coils, thus explaining why one of these coils the first to break. High-carbon spring steel do not withstand shock loading as well as the alloy steels. Breakage does not occurs often because the spring are not subjected to the service required in racing cars, and one or two coils are aslo made at a reduced pitch to alter the natural period of vibration cause by rapid loading.

5) Faulty heat treatment 6) Non-central loading 7) High temperatures

Investigation of the application of a spring usually determines if it was subjected to elevated temperatures. A discoloration of the suface finish or an accumulation of a sooty crust may be evident. A blue color may be observed at the cutoff ends of the steel springs. If the stress is low but a permenant set occurred, it also may be evidence of a high-temperature application.

8) Low temperatures

Sub zero-temperature are usually determined by discussion with the customer. Brittle fractures may occur at a right angle to the longitudinal section or at any angle; some fractures are even jagged with sharp edges, and more than one fracture may be evident.

9) Friction

A wearing away of the material due to friction is easily observed visually, in the same manner as finding cracks, seams, and slivers.

10) Welding

The high heat caused by welding destroys the temper of a spring and alters the grains structure. Tack welding of the end coil to hold a spring in a desired position may be done, but it is useless to weld together the parts of the broken spring.

11) Tool marks

Tools for making bends should not have sharp edges. Tool marks on the inside of bends are stress raisers. They are easily discernible visually and should be avoided.

Reduction of failures

1. Shotpeening
2. Heat treatment
3. Presetting

References

1. ^ Springs How Products Are Made, 14 July 2007.
2. ^ ^{a b} White, Lynn Jr. (1966). Medieval Technology and Social Change. New York: Oxford Univ. Press. ISBN 0195002660. , p.126-127
3. ^ Usher, Abbot Payson (1988). A History of Mechanical Inventions. Courier Dover. ISBN 048625593X. http://books.google.com/books?id=xuDDqqa8FlwC&pg=PA305. , p.305
4. ^ Dohrn-van Rossum, Gerhard (1997). History of the Hour: Clocks and Modern Temporal Orders. Univ. of Chicago Press. ISBN 0-226-15510-2. http://books.google.com/books?id=53K32RiEigMC&pg=PA121. , p.121
5. ^ Carlson, Harold. Spring Manufacturing Handbook. Marcel Dekker, Inc.. p. 43. ISBN 0-8147-1678-7. http://books.google.com/books/about/Spring_Manufacturing_Handbook.html?id=E3ywPAAACAAJ. 
6. ^ Samuel, Andrew; Weir, John (1999). Introduction to engineering design: modelling, synthesis and problem solving strategies (2 ed.). Oxford, England: Butterworth. p. 134. ISBN 0750642823. 
7. ^ Davis, Thomas Beiber; Nelson, Carl A. Senior. Audel Mechanical Trades Pocket Manual (4 ed.). Hoboken, NJ: Wiley. p. 275. ISBN 978-0-7645-4170-4. 
8. ^ Faires, Virgil Moring. Design of machine elements. Macmillan. p. 165. ISBN 0-02-335950-1. http://books.google.com/books?id=0BMzAAAAMAAJ. 
9. ^ "Lucien LaCoste Suspension". Lucien LaCoste. http://web.me.com/patandmel/UTexas_Physics_History/Lucien_LaCoste.html. Retrieved 29 August 2011. 
10. ^ Carlson, Harold. Spring Troubleshooting and Failure Analysis. Marcel Dekker, Inc.. p. 131. ISBN 0-8247-1003-7. 

External links

• Wright, Douglas. "Introduction to Springs". Springs, Notes on Design and Analysis of Machine Elements. Deptartment of Mechanical & Material Engineering, University of Western Australia. http://www.mech.uwa.edu.au/DANotes/springs/intro/intro.html. Retrieved 2008-02-03. 
• Silberstein, Dave (2002). "How to make springs". Bazillion. http://home.earthlink.net/~bazillion/intro.html. Retrieved 2008-02-03.