- Wikipedia:Manual of Style/Mathematics
-

This guideline is a part of the English Wikipedia's Manual of Style. Use common sense in applying it; it will have occasional exceptions. Please ensure that any edits to this page reflect consensus. Manual of Style Arts- Anime & Manga
- Comics
- Film
- Lyrics and Poetry
- Novels
- Television
- Visual arts
- Writing about fiction
Content- Accessibility
- Article message boxes
- Biographies
- Disambiguation pages
- Infoboxes
- Linking
- Self-references
- Words to watch
Dates and numbers- Dates and numbers
Formatting- Abbreviations
- Capitalization
- Dates and numbers
- Pronunciation
- Proper names
- Spelling
- Text formatting
- Titles
Images- Captions
- Galleries
- Icons
- Images
- Layout
Layout- Footnotes
- Layout
- Lead section
- Tables
- Trivia sections
Lists- Embedded lists
- Lists of works
- Lists
- Road junctions
Legal- Legal
- Trademarks
Music- Music
- Samples
- Record charts
Regional- Canada
- France
- Hawaii
- Ireland
- Japan
- Philippine
- Poland
Religion- Islam
- Latter Day Saints
Science- Chemistry
- Mathematics
- Medicine
- Computer commands
- Taxonomy
Sports- Cue sports
- Snooker more specifically
Related guidelines- Article size
- Article titles
- Categories, lists, and navigation templates
- Categorization
- Footnotes
- Template namespace
- Hatnotes
- Signatures
- Talk page guidelines
- Subpages
- User pages
This subpage of the Manual of Style contains guidelines for writing and editing clear, encyclopedic, attractive, and interesting articles on mathematics. For matters of style not treated on this subpage, follow the main Manual of Style and its other subpages to achieve consistency of style throughout Wikipedia.
Suggested structure of a mathematics article
Probably the hardest part of writing a mathematical article (actually, any article) is the difficulty of addressing the level of mathematical knowledge on the part of the reader. For example, when writing about a field, do we assume that the reader already knows group theory? A general approach is to start simple, then move toward more abstract and technical statements as the article proceeds.
Article introduction
See also: WP:Manual of Style (lead section)The article should start with a short introductory section (often referred to as the lead). The purpose of this section is to describe, define, and give context to the subject of the article, to establish why it is interesting or useful, and to summarize the most important points. The lead should as far as possible be accessible to a general reader, so specialized terminology and symbols should be avoided as much as possible.
In general, the lead sentence should include the article title in bold along with alternate names, establish context by linking to a more general subject, and informally define or describe the subject. For example:
Topology (from the Greek τόπος, “place”, and λόγος, “study”) is a major area of mathematics concerned with spatial properties that are preserved under continuous deformations of objects, for example, deformations that involve stretching, but no tearing or gluing.
In Euclidean plane geometry, Apollonius' problem is to construct circles that are tangent to three given circles in a plane.
The lead section should include, where appropriate:
- Historical motivation, including names and dates, especially if the article does not have a separate History section. Explain the origin of the name if it is not self-evident.
- An informal introduction to the topic, without rigor, suitable for a general audience. (The appropriate audience for the overview will vary by article, but it should be as basic as reasonable.) The informal introduction should clearly state that it is informal, and that it is only stated to introduce the formal and correct approach. If a physical or geometric analogy or diagram will help, use one: many of the readers may be non-mathematical scientists.
- Motivation or applications, which can illuminate the use of the mathematical idea and its connections to other areas of mathematics.
Article body
If you want to introduce some notation, it should be in its own section. You should remember that not everyone understands that, for example, x^n or x**n mean xn; so it is good to use standard notation if you can. If you need to use non-standard notations, or if you introduce new notations, define them in your article.
There should be an exact definition, in mathematical terms; often in a Definition(s) section, for example:
Let S and T be topological spaces, and let f be a function from S to T. Then f is called continuous if, for every open set O in T, the preimage f −1(O) is an open set in S.
Using the term formal definition may seem rather empty to a mathematician (a formal definition is a mathematician's definition, as a formal proof is just a proof); but it may help to flag where the actual definition is to be found, after some sections of motivation. (Cf. rigged Hilbert space.)
Some representative examples would be nice to have, in a separate section, which could serve to both expand on the definition, and also provide some context as to why one might want to use the defined entity. You might also want to list non-examples—things which come close to satisfying the definition but do not—in order to refine the reader's intuition more precisely. It is important to remember when composing examples, however, that the purpose of an encyclopedia is to inform rather than instruct (see WP:NOT#TEXTBOOK). Examples should therefore strive to maintain an encyclopedic tone, and should be informative rather than merely instructional.
A picture is a great way of bringing a point home, and often it could even precede the mathematical discussion of a concept. How to create graphs for Wikipedia articles has some hints on how to create graphs and other pictures, and how to include them in articles.
A person editing a mathematics article should not fall into the temptation that "this formula says it all". A non-mathematical reader will skip the formulae in most cases, and often a mathematician reading outside her or his research area will do the same. Careful thought should be given to each formula included, and words should be used instead if possible. In particular, the English words "for all", "exists", and "in" should be preferred to the ∀, ∃, and ∈ symbols. Similarly, highlight definitions with words such as "is defined by" in the text.
If not included in the introductory paragraph, a section about the history of the concept is often useful and can provide additional insight and motivation.
Concluding matters
Most mathematical ideas are amenable to some form of generalization. If appropriate, such material can be put under a Generalizations section. As an example, multiplication of the rational numbers can be generalized to other fields, etc.
It is good to have a see also section, which connects to related subjects, or to pages which could provide more insight into the contents of the current article.
Lastly, a well-written and complete article should have a references section. This topic will be discussed in detail below.
Writing style in mathematics
There are several issues of writing style that are particularly relevant in mathematical writing.
- In the interest of clarity, sentences should not begin with a symbol. Here are some examples of what not to do:
-
- Suppose that G is a group. G can be decomposed into cosets, as follows.
- Let H be the corresponding subgroup of G. H is then finite.
- Instead, one could write this:
- A group G may be decomposed into cosets as follows.
- Let H be the corresponding subgroup of G. Then H must be finite.
- Mathematics articles are often written in a conversational style, as if a lecture is being presented to the reader, and the article is taking the place of the lecturer's whiteboard. However, an article that "speaks" to the reader runs counter to the ideal encyclopedic tone of most Wikipedia articles. Article authors should avoid referring to "we" or addressing the reader directly. While opinions vary on how far this guideline should be taken in mathematics articles—an encyclopedic tone can make advanced mathematical topics more difficult to learn—authors should try to strike a balance between simply presenting facts and formulae, and relying too much on directing the reader or using such clichés as
- "Note that…" / "It should be noted that…"
- "It must be mentioned that…" / "It must be emphasized that…"
- "Consider that…"
- "We see that…"
- and so on. Such introductory phrases are often unnecessary and can be omitted without affecting semantics. Rather than repeatedly attempting to draw the reader's attention to crucial pieces of information that have been appended almost as an afterthought, try to reorganize and rephrase the material such that crucial information comes first. There also should be no doubt as to the reader's willingness to continue reading and taking note of whatever information is presented; the reader does not need to be implored to take note of each thing being pointed out.
- The articles should be accessible, as much as possible, to readers not already familiar with the subject matter. Notations that are not entirely standard should be properly introduced and explained. Whenever a variable or other symbol is defined in a formula, make sure that it is clear that this is a definition introducing a notation, and not, for example, just another equation. Also identify the nature of the entity being defined. So don't write this:
-
- Multiplying M by u = v − v0, ...
- Instead, write:
- Multiplying M by the vector u defined by u = v − v0, ...
- In definitions, the symbol "=" is preferred over "≡" or ":=".
- When defining a term, do not use the phrase "if and only if". For example, instead of
-
- A function f is even if and only if f( − x) = f(x) for all x
- write
- A function f is even if f( − x) = f(x) for all x.
- If it is reasonable to do so, rephrase the sentence to avoid the use of the word "if" entirely. For example,
- An even function is a function f such that f( − x) = f(x) for all x.
- Avoid, as far as possible, phrases such as
- "It is easily seen that ..."
- "Clearly ..."
- "Obviously ..."
- The reader might not find what you write obvious. This kind of statement does not add new information and thus detracts from the clarity of the article. Instead, it may be helpful to the reader if a hint is provided as to why something must hold, such as:
-
- "It follows directly from this definition that ..."
- "By a straightforward, if lengthy, algebraic calculation, ..."
- When lecturing using a blackboard, it is common to use abbreviations including wrt (with regard to) and wlog (without loss of generality), and to use quantifier symbols ∀ and ∃ instead of for all and there exists in prose. Some authors, including Paul Halmos, use the abbreviation iff for if and only if in print. On Wikipedia, all such abbreviations should be avoided. In addition to compromising the formal tone expected of an encyclopedia, these abbreviations are a form of jargon that may be unfamiliar to the reader.
- The plural of formula is either formulae or formulas. Both are acceptable, but articles should be consistent with themselves. If an article is consistent, then editors should not change the article from one style to another.
Mathematical conventions
See also: Wikipedia:WikiProject Logic/Standards for notationA number of conventions have been developed to make Wikipedia's mathematics articles more consistent with each other. These conventions cover choices of terminology, such as the definitions of compact and ring, as well as notation, such as the correct symbols to use for a subset.
These conventions are suggested in order to bring some uniformity between different articles, to aid a reader who moves from one article to another. However, each article may establish its own conventions. For example, an article on a specialized subject might be more clear if written using the conventions common in that area. Thus the act of changing an article from one set of conventions to another should not be undertaken lightly.
Each article should explain its own terminology as if there are no conventions, in order to minimize the chance of confusion. Not only do different articles use different conventions, but Wikipedia's readers come to articles with widely different conventions in mind. These readers will often not be familiar with our conventions, which may differ greatly from the conventions they see outside Wikipedia. Moreover, when our articles are presented in print or on other websites, there may be no simple way for readers to check what conventions have been employed.
Terminology conventions
- A compact space is not assumed to be Hausdorff (contra Bourbaki, who uses quasi-compact for our notion of compactness).
- Separation axioms for topological spaces are as described on the separation axiom page.
- A ring is assumed to be associative and unital. There is an exception for rings of operators, such as * algebras, B* algebras, C* algebras, which we do not assume to be unital.
- A local ring is not assumed noetherian (contra Zariski).
- A scheme (mathematics) is not assumed to be separated. The term "prescheme" is not used.
- For Clifford algebras use v2 = +Q(v).
- A weight k modular form follows the Serre convention that f(−1/τ) = τkf(τ), and q = e2πiτ.
- Elliptic functions are written in ω = half-period style.
- Directed sets are preordered sets with finite joins, not partial orders as in, e.g., Kelley (General Topology; ISBN 0-387-90125-6).
- An algebraic variety is assumed to be an irreducible algebraic set.
- A lattice need not be bounded. In a bounded lattice, 0 and 1 are allowed to be equal.
Natural numbers
The set of natural numbers has two common meanings: {0, 1, 2, 3, ...}, which may also be called non-negative integers, and {1, 2, 3, ...}, which may also be called positive integers. Use the sense appropriate to the field to which the subject of the article belongs if the field has a preferred convention. If the sense is unclear, and if it is important whether or not zero is included, consider using one of the alternative phrases rather than natural numbers if the context permits.
Notational conventions
- The abstract cyclic group of order n, when written additively, has notation Zn, or in contexts where there may be confusion with p-adic integers, Z/nZ; when written multiplicatively, e.g. as roots of unity, Cn is used (this does not affect the notation of isometry groups called Cn).
- The standard notation for the abstract dihedral group of order 2n is Dn in geometry and D2n in finite group theory. There is no good way to reconcile these two conventions, so articles using them should make clear which they are using.
- Bernoulli numbers are denoted by Bn, and are zero for n odd and greater than 1.
- In category theory, write Hom-sets, or morphisms from A to B, as Hom(A,B) rather than Mor(A,B) (and with the implied convention that the category is not a small category unless that is said).
- The semidirect product of groups K and Q should be written K ×φ Q or Q ×φ K where K is the normal subgroup and φ : Q → Aut(K) is the homomorphism defining the product. The semidirect product may also be written K ⋊ Q or Q ⋉ K (with the bar on the side of the non-normal subgroup) with or without the φ.
- The context should clearly state that this is a semidirect product and should state which group is normal.
- The bar notation is discouraged because it is not supported by all browsers.
- If the bar notation is used it should be entered as {{unicode|⋉}} (⋉) or {{unicode|⋊}} (⋊) for maximum portability.
- Subset is denoted by
 , proper subset by
, proper subset by  . The symbol
. The symbol  may be used if the meaning is clear from context, or if it is not important whether it is interpreted as subset or as proper subset (for example,
may be used if the meaning is clear from context, or if it is not important whether it is interpreted as subset or as proper subset (for example,  might be given as the hypothesis of a theorem whose conclusion is obviously true in the case that A = B). All other uses of the
might be given as the hypothesis of a theorem whose conclusion is obviously true in the case that A = B). All other uses of the  symbol should be explicitly explained in the text.
symbol should be explicitly explained in the text. - For a matrix transpose, use superscript non-italic capital letter T: XT, XT or
 , and not XT, XT,
, and not XT, XT,  or
or  .
. - In a lattice, infima are written as a ∧ b or as a product ab, suprema as a ∨ b or as a sum a + b. In a pure lattice theoretical context the first notation is used, usually without any precedence rules. In a pure engineering or "ideals in a ring" context the second notation is used and multiplication has higher precedence than addition. In any other context the confusion of readers of all backgrounds should be minimized. In an abstract bounded lattice, the smallest and greatest elements are denoted by 0 and 1.
Proofs
This is an encyclopedia, not a collection of mathematical texts; but we often want to include proofs, as a way of really exposing the meaning of some theorem, definition, etc. A downside of including proofs is that they may interrupt the flow of the article, whose goal is usually expository. Use your judgement; as a rule of thumb, include proofs when they expose or illuminate the concept or idea; don't include them when they serve only to establish the correctness of a result.
Since many readers will want to skip proofs, it is a good idea to set them apart in some way, for instance by giving them a separate section. Additional discussion and guidelines can be found at Wikipedia:WikiProject Mathematics/Proofs.
Algorithms
See also: Wikipedia:WikiProject Computer science/Manual of style (computer_science)#AlgorithmsAn article about an algorithm may include pseudocode or in some cases source code in some programming language. Wikipedia does not have a standard programming language or languages, and not all readers will understand any particular language even if the language is well-known and easy to read, so consider whether the algorithm could be expressed in some other way. If source code is used always choose a programming language that expresses the algorithm as clearly as possible.
Articles should not include multiple implementations of the same algorithm in different programming languages unless there is encyclopedic interest in each implementation.
Source code should always use syntax highlighting. For example this markup:[1]
<source lang="Haskell"> primes = sieve [2..] sieve (p : xs) = p : sieve [x | x <- xs, x `mod` p > 0] </source>
generates the following:
primes = sieve [2..] sieve (p : xs) = p : sieve [x | x <- xs, x `mod` p > 0]
Including literature and references
It is quite important for an article to have a well-chosen list of references and pointers to the literature. Some reasons for this are the following:
- Wikipedia articles cannot be a substitute for a textbook (that is what Wikibooks is for). Also, often one might want to find out more details (like the proof of a theorem stated in the article).
- Some notions are defined differently depending on context or author. Articles should contain some references that support the given usage.
- Important theorems should cite historical papers as an additional information (not necessarily for looking them up).
- Today many research papers or even books are freely available online and thus virtually just one click away from Wikipedia. Newcomers would greatly profit from having an immediate connection to further discussions of a topic.
- Providing further reading enables other editors to verify and to extend the given information, as well as to discuss the quality of a particular source.
The Wikipedia:cite sources article has more information on this and also several examples for how the cited literature should look.
Typesetting of mathematical formulae
See also: Help:Displaying a formulaOne may set formulae using LaTeX or, for simple formulae, using HTML; both are acceptable and widely used, though there are issues, as discussed below. However, for section headings, use HTML only, as LaTeX markup does not appear in the table of contents.
Using LaTeX markup
Wikipedia allows editors to typeset mathematical formulas in (a subset of) LaTeX markup (see also TeX); the formulae are normally translated into PNG images, but may be rendered as HTML or MathML, depending on user preferences. For more details on this, see meta:Help:Formula.
The LaTeX formulae can be displayed in-line (like this:
 ), as well as on their own line:
), as well as on their own line:When displaying formulae on their own line, one should indent the line with one or more colons (:); the above was typeset from
:<math>\int_0^\infty e^{-x^2}\,dx.</math>
If you find an article which indents lines with spaces in order to achieve some formula layout effect, you should convert the formula to LaTeX markup.
Having LaTeX-based formulae in-line which render as PNG under the default user settings, as above, is generally discouraged, for the following reasons.
- The font size is larger than that of the surrounding text on some browsers, making text containing in-line formulae hard to read.
- Misalignment can result. For example, instead of ex, with "e" at the same level as the surrounding text and the x in superscript, one may see the e lowered to put the vertical center of the whole "ex" at the same level as the center of the surrounding text.
- The download speed of a page is negatively affected if it contains many images.
- HTML (as described below) is adequate for most simple in-line formulae and better for text-only browsers.
If an in-line formula needs to be typeset in LaTeX, often better formatting can be achieved with the
\textstyleLaTeX command. By default, LaTeX code is rendered as if it were a displayed equation (not in-line), and this can frequently be too big. For example, the formula<math>\sum_{n=1}^\infty 1/n^2 = \pi^2/6 </math>, which displays as , is too large to be used in-line.
, is too large to be used in-line. \textstylegenerates a smaller summation sign and moves the limits on the sum to the right side of the summation sign. The code for this is<math>\textstyle\sum_{n=1}^\infty 1/n^2 = \pi^2/6</math>, and it renders as the much more aesthetic . However, the default font for
. However, the default font for \textstyleis larger than the surrounding text on many browsers.If you plan on editing LaTeX formulae, it is helpful if you leave your preference settings (link in the upper right corner of this page, underneath your user name) in the "rendering math" section at the default "HTML if very simple or else PNG"; that way, you'll see the page like most users will see it.
Very simple formulae
If you enter a very simple formula using the mathematical notations like
<math>L^p</math>this will (in the default used by most users) not be displayed using a PNG image but using HTML, like this: Lp. This is different from typesetting it as''L''<sup>''p''</sup>. Compare:-
LaTeX rendered as HTML: Lp Regular HTML: Lp .
Either form is acceptable, but do not change one form to the other in other people's writing. They are likely to get annoyed since this seems to be a highly emotional issue. Changing to make an entire article consistent is acceptable.
However, still try to avoid in-line PNG images. Even if you use
<math>L^p</math>throughout the article, use''L''<sup>∞</sup>to get L∞ rather than using the LaTeX-based<math>L^\infty</math>to get , which doesn't always look good.
, which doesn't always look good.Forcing output to be an image
If you want to force a formula to be displayed as an image, put, for example, a
\,(one quarter space in LaTeX) at the end of the formula. This should usually only be done for formulae displayed on their own line. Adding\displaystyleat the beginning of the formula has the same effect.Alt text
Images generated from LaTeX markup have alt text, which is displayed to visually impaired readers and other readers who cannot see the images. The default alt text is the LaTeX markup that produced the image. You can override this by explicitly specifying an
altattribute for themathelement. For example,<math alt="Square root of pi">\sqrt{\pi}</math>generates an image whose alt text is "Square root of pi". Small and easily explained formulas used in less technical articles can benefit from explicitly specified alt text. More complicated formulas, or formulas used in more technical articles, are often better off with the default alt text.
whose alt text is "Square root of pi". Small and easily explained formulas used in less technical articles can benefit from explicitly specified alt text. More complicated formulas, or formulas used in more technical articles, are often better off with the default alt text.Using HTML
The following sections cover the way of presenting simple in-line formulae in HTML, instead of using LaTeX.
Templates supporting HTML formatting are listed in Category:Mathematical formatting templates. Not all however are recommended for use, in particular use of the {{frac}} template to format fractions is discouraged in mathematics articles.
Font formatting
''x'' = (''y''<sup>2</sup> + 2)
will result in:
- x = (y2 + 2) .
As TeX uses a serif font to display a formula (both as PNG and HTML), you may use the {{math}} template to display your HTML formula in serif as well. Doing so will also ensure that the text within a formula will not line-wrap, and that the font size will closely match the surrounding text in any skin.
{{math|''x'' {{=}} (''y''<sup>2</sup> + 2)}}
will result in:
- x = (y2 + 2) .
Variables
To start with, we generally use italic text for variables (but never for numbers or symbols). Most editors prefer to use
''x''in the edit box to refer to the variable x. Some prefer using the HTML "variable" tag,<var>, since it provides semantic meaning to the text contained within. Which method you choose is entirely up to you, but in order to keep with convention, we recommend the wiki markup method of enclosing the variable name between repeated single quotes. Thus we write:''x'' = (''y''<sup>2</sup> + 2),
which results in:
- x = (y2 + 2) .
While italicizing variables, things like parentheses, digits, equal and plus signs should be kept outside of the double-quoted sections. In particular, do not use double quotes as if they are
<math>tags; they merely denote italics. Descriptive subscripts should not be in italics, because they are not variables. For example, mfoo is the mass of a foo. SI units are never italicized: x = 5 cm.Functions
Names for standard functions, such as sin and cos, are not in italic font, but we use italic names such as f for functions in other cases; for example when we define the function as in f(x) = sin(x) cos(x).
Sets
Sets are usually written in upper case italics; for example:
- A = {x : x > 0 }
would be written:
''A'' = {''x'' : ''x'' > 0}.
Greek letters
Some editors italicize lower-case Greek letters when they are variables (in line with the general advice to italicize variables): the example expression λ + y = πr2 would then be typeset as
''λ'' + ''y'' = ''πr''<sup>2</sup>. However the examples in the other sections of this guide do not specify italic formatting of Greek letters.Common sets of numbers
Commonly used sets of numbers are typeset in boldface, as in the set of real numbers R; see blackboard bold for the types in use. Again, typically we use wiki markup: three single quotes (
''') rather than the HTML<b>tag for making text bold.Superscripts and subscripts
Main page: Wikipedia:Manual of Style (superscripts and subscripts)Subscripts and superscripts should be wrapped in
<sub>and<sup>tags, respectively, with no other formatting info. Font sizes and such should be entrusted to be handled with stylesheets. For example, to write c3+5, use''c''<sub>3+5</sub>.
Do not use special characters like ² (
²) for squares. This does not combine well with other powers, as the following comparison shows:- 1 + x + x² + x3 + x4 (with
²) versus - 1 + x + x2 + x3 + x4 (with
<sup>2</sup>).
Moreover, the TeX engine used on Wikipedia may format simple superscripts using
<sup>...</sup>depending on user preferences. Thus, instead of the image , many users see x2. Formulae formatted without using TeX should use the same syntax to maintain the same appearance.
, many users see x2. Formulae formatted without using TeX should use the same syntax to maintain the same appearance.Special symbols
There is a table of mathematical symbols and a list at Wikipedia:Mathematical symbols that may be useful when editing mathematics articles. There are two caveats to keep in mind, however.
- Not all of the symbols in these lists are displayed correctly on all browsers (see Help:Special characters). Although the symbols that correspond to named entities are very likely to be displayed correctly, a significant number of viewers will have problems seeing all the characters listed at Unicode Mathematical Operators. One way to guarantee that an uncommon symbol is rendered correctly for all readers is to force the symbol to display as an image, using the <math> environment.
- Not all readers will be familiar with mathematical notation. Thus, to maximize the size of the audience who can read an article, it is better to be conservative in using symbols. For example, writing "a divides b" rather than "a|b" in an elementary article may make it more accessible.
Less-than sign
Although the MediaWiki markup engine is fairly smart about differentiating between unescaped "<" characters that are used to denote the start of an embedded HTML or HTML-like tag and those that are just being used as literal less-than symbols, it is ideal to use
<when writing the less-than sign, just like in HTML and XML. For example, to write x < 3, use''x'' < 3,
not
''x'' < 3.
Multiplication sign
Standard algebraic notation is best for formulae, so two variables q and d being multiplied are best written as qd when presented in a formula. That is, when citing a formula, don't use
×.However, when explaining, for a general audience (not just mathematicians), the formula or giving examples of its application, it is prudent to use the multiplication sign: "×", coded as
×in HTML. Do not use the letter "x" as a substitute for "×". For example:- When dividing 26 by 4, 6 is the quotient and 2 is the remainder, because 26 = 6 × 4 + 2.
- −42 = 9 × (−5) + 3
Another alternative to the
×markup is·, which will produce a center dot: " · ".Minus sign
The typographically correct representation of the minus sign "−" is different from the hyphen "-" and en-dash "–". To really render a minus sign, use the "minus" character "−" (reachable via selecting "Math and logic" in the "Choose character subset" drop down list below the edit box), or use the "−" entity.
Square brackets
Square brackets have two problems; they can occasionally cause problems with wiki markup, and editors sometimes 'fix' the brackets in asymmetrical intervals to make them symmetrical. A general solution to problems like this is to use the nowiki tag as in for example
<nowiki>]<nowiki>to show ] is special.The use of intervals for the range or domain of a function is very common. A solution which makes the reason for the different brackets around an interval more plain is to use one of the templates {{open-closed}}, {{closed-open}}, {{open-open}}, {{closed-closed}}. For instance:
{{open-closed|−π, π}},
produces
- (−π, π].
These templates use the {{math}} template to avoid line breaks and use the TeX font.
Function symbol
There is a special Unicode function symbol for functions, U+0192, "LATIN SMALL LETTER F WITH HOOK = script f = Florin currency symbol (Netherlands) = function symbol"[2], which looks like ƒ. As of December 2010, this character is not interpreted correctly by screen readers such as JAWS and NonVisual Desktop Access[3]. An italicized letter f should be used instead.
Explanation of symbols in formulae
A list such as:
Example 1: The foocity is given by
- b is the barness vector,
- a is the bazness coefficient,
- r is the quuxance vector.
has no reason to be bulleted, and it should be written as prose:
Example 2: The foocity is given by
An exception would be if some of the definitions are very long (for example, as in Heat equation), but, even in this case, each definition should end with a comma or semicolon, and the last one should end with a period if it terminates a sentence.
Punctuation after formulae
Just as in mathematics publications, a sentence which ends with a formula must have a period at the end of the formula.[4] This equally applies to displayed formulae (that is, formulae that take up a line by themselves). Similarly, if the conventional punctuation rules would require a question mark, comma, semicolon, or other punctuation at that place, the formula must have that punctuation at the end.
If the formula is written in LaTeX, that is, surrounded by the
<math>and</math>tags, then the punctuation needs to also be inside the tags, because otherwise it can be displayed on a new line if the formula is at the edge of the browser window. Alternatively—the result can be unaesthetic, especially for inlined formulae presented as an image whose baseline does not line up with that of the running text—the formula can be enclosed using the {{nowrap}} template, as inThis shows that {{nowrap|<math>\tfrac{1}{2} = 0.5</math>.}}.Choice of type style
In mathematics notation, functions that have multi-letter names should always be in an upright font. The most well-known functions—trigonometric functions, logarithms, etc.—have no parentheses. For example:
 (correct typeset from
(correct typeset from <math>\sin x \,\!</math>)
but not
 (incorrect—typeset from
(incorrect—typeset from <math>sin x \,\!</math>).
Some operator (function) names do not have a pre-defined abbreviation; for these we may use
\operatorname: (typeset from
(typeset from <math>\operatorname{Tr}(M) \,\!</math>).
Special care is needed with subscripted labels to distinguish the purpose of the subscript (as this is a common error): variables and constants in subscripts should be italic, while textual labels should be in normal text font (Roman, upright). For example:
 (correct—typeset from
(correct—typeset from <math> x_\text{this one} = y_\text{that one} \,\!</math>),
and
 (correct—typeset from
(correct—typeset from <math>\sum_{i=1}^n { y_i^2 }\!</math>),
but not
- r = xpredicted − xobserved (incorrect—typeset from
<math>r = x_{predicted} - x_{observed}</math>).
-
- For several years this manual misled people concerning \mbox. See An opinion: Why you should never use \mbox within Wikipedia.
On the other hand, for the differential, imaginary unit, and Euler's number, Wikipedia articles usually use an italic font, so one writes
 (typeset from
(typeset from <math>\int_0^\pi \sin x \, dx , \,\!</math>—note the thin space (\,) beforedx), (typeset from
(typeset from <math>x+iy, \,\!</math>), and (typeset from
(typeset from <math>e^{i\theta} . \,\!</math>).
Some authors prefer to use an upright (Roman) font for dx, and Roman boldface for i. Both forms are correct; what is most important is consistency within an article, with deference to previous editors. It is considered inappropriate for an editor to go through articles doing mass changes from one style to another. This is much the same principle as the guidelines in the Manual of Style for the colour/color spelling choice, etc.
Blackboard bold
Certain objects, such as the real numbers R, are traditionally printed in boldface. On a blackboard or a whiteboard, boldface type is replaced by blackboard bold. Traditional mathematical typography never used printed blackboard bold because it is harder to read than ordinary boldface. Nowadays, however, some printed books and articles use blackboard bold. A particular concern for the use of blackboard bold on Wikipedia is that these symbols must be rendered as images because the Unicode symbols for blackboard bold characters are not supported by all systems.
An article may use either boldface type or blackboard bold for objects traditionally printed in boldface. As with all such choices, the article should be consistent. Editors should not change articles from one choice of typeface to another except for consistency.
Fractions
See also: Wikipedia:Manual of Style (dates and numbers)#FractionsIn mathematics articles, fractions should always be written either with a horizontal fraction bar (as in
 ), or with a forward slash and with the baseline of the numbers aligned with the baseline of the surrounding text (as in 1/2). The use of {{frac}} (such as 1⁄2) is discouraged in mathematics articles. The use of Unicode symbols (such as ½) is discouraged entirely, for accessibility reasons among others. Metric units are given in decimal fractions (e.g., 5.2 cm); non-metric units can either type of fraction, but the fraction style should be consistent throughout the article.
), or with a forward slash and with the baseline of the numbers aligned with the baseline of the surrounding text (as in 1/2). The use of {{frac}} (such as 1⁄2) is discouraged in mathematics articles. The use of Unicode symbols (such as ½) is discouraged entirely, for accessibility reasons among others. Metric units are given in decimal fractions (e.g., 5.2 cm); non-metric units can either type of fraction, but the fraction style should be consistent throughout the article.Graphs and diagrams
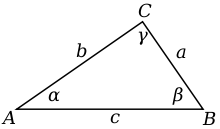
There is no general agreement on what fonts to use in graphs and diagrams. In geometrical diagrams points are normally labelled using upper case letters, sides with lower case and angles with lower case Greek letters.
Recent geometry books tend to use an italic serif font in diagrams as in A for a point. This allows easy use in LaTeX markup. However older books tend to use upright letters as in A and many diagrams in Wikipedia use sans-serif upright A instead. Graphs in books tend to use LaTeX conventions, but yet again there are wide variations.
For ease of reference diagrams and graphs should use the same conventions as the text that refers to them. If there is a better illustration with a different convention though the better illustration should normally be used.
See also
Help for those writing a formula
- Help:Formula
- Wikipedia:Mathematical symbols
General information
- Wikipedia:WikiProject Mathematics
- Wikipedia:Scientific citation guidelines—advice on providing references for mathematical and scientific articles
Notes
- ^ This example, from here [1], is in Haskell, not a well-known language so generally not a good choice when showing an algorithm.
- ^ Latin Extended-B, [2]
- ^ Wikipedia talk:WikiProject Mathematics/Archive 68#ƒ or f?
- ^ This style, adopted by Wikipedia, is shared by Higham (1998), the Chicago Manual of Style, and many mathematics journals.
Further reading
A style guide specifically written for mathematics:
- Higham, Nicholas J. (1998), Handbook of Writing for the Mathematical Sciences (second ed.), SIAM, ISBN 0-89871-420-6.
More style guidance:
- Halmos, P.R. (1970), "How to Write Mathematics", Enseignements Mathématiques 16: 123–152. Reprinted in ISBN 0821800558
Some finer points of typography are discussed in:
- Knuth, Donald E. (1984), The TeXbook, Reading, Massachusetts: Addison-Wesley, ISBN 0-201-13448-9.
General style manuals often include advice on mathematics, including
- University of Chicago Press Staff, ed. (2010), The Chicago Manual of Style (16th ed.), University of Chicago Press, ISBN 9780226104201, http://www.chicagomanualofstyle.org/home.html
Categories:- WikiProject Mathematics
- Wikipedia how-to
- Wikipedia Manual of Style (science)
Wikimedia Foundation. 2010.