Strength of materials

Internal force lines are denser near the hole, a common stress concentration

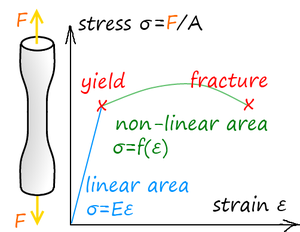
In materials science, the strength of a material is its ability to withstand an applied stress without failure. The applied stress may be tensile, compressive, or shear. Strength of materials is a subject which deals with loads, deformations and the forces acting on a material. A load applied to a mechanical member will induce internal forces within the member called stresses. The stresses acting on the material cause deformation of the material. Deformation of the material is called strain, while the intensity of the internal forces is called stress. The strength of any material relies on three different type of analytical method: strength, stiffness and stability, where strength refers to the load carrying capacity, stiffness refers to the deformation or elongation, and stability refers to the ability to maintain its initial configuration. Material yield strength refers to the point on the engineering stress-strain curve (as opposed to true stress-strain curve) beyond which the material experiences deformations that will not be completely reversed upon removal of the loading. The ultimate strength refers to the point on the engineering stress-strain curve corresponding to the stress that produces fracture.

A material's strength is dependent on its microstructure. The engineering processes to which a material is subjected can alter this microstructure. The variety of strengthening mechanisms that alter the strength of a material includes work hardening, solid solution strengthening, precipitation hardening and grain boundary strengthening and can be quantitatively and qualitatively explained. Strengthening mechanisms are accompanied by the caveat that some mechanical properties of the material may degenerate in an attempt to make the material stronger. For example, in grain boundary strengthening, although yield strength is maximized with decreasing grain size, ultimately, very small grain sizes make the material brittle. In general, the yield strength of a material is an adequate indicator of the material's mechanical strength. Considered in tandem with the fact that the yield strength is the parameter that predicts plastic deformation in the material, one can make informed decisions on how to increase the strength of a material depending its microstructural properties and the desired end effect. Strength is expressed in terms of compressive strength, tensile strength, and shear strength, namely the limit states of compressive stress, tensile stress and shear stress, respectively. The effects of dynamic loading are probably the most important practical consideration of the strength of materials, especially the problem of fatigue. Repeated loading often initiates brittle cracks, which grow until failure occurs. The cracks always start at stress concentrations, especially changes in cross-section of the product, near holes and corners.

The study of the subject of strength of materials often refers to various methods of calculating stresses in structural members, such as beams, columns and shafts. The methods employed to predict the response of a structure under loading and its susceptibility to various failure modes may take into account various properties of the materials other than material (yield or ultimate) strength. For example failure in buckling is dependent on material stiffness (Young's Modulus).

Types of loadings

• Transverse loading - Forces applied perpendicular to the longitudinal axis of a member. Transverse loading causes the member to bend and deflect from its original position, with internal tensile and compressive strains accompanying the change in curvature of the member.^[1] Transverse loading also induces shear forces that cause shear deformation of the material and increase the transverse deflection of the member.
• Axial loading - The applied forces are collinear with the longitudinal axes of the member. The forces cause the member to either stretch or shorten.^[2]
• Torsional loading - Twisting action caused by a pair of externally applied equal and oppositely directed force couples acting on parallel planes or by a single external couple applied to a member that has one end fixed against rotation.

Definitions

Stress terms

A material being loaded in a) compression, b) tension, c) shear.

Uniaxial stress is expressed by

$\sigma=\frac{F}{A},$

where F is the force [N] acting on an area A [m²].^[3] The area can be the undeformed area or the deformed area, depending on whether engineering stress or true stress is of interest.

• Compressive stress (or compression) is the stress state caused by an applied load that acts to reduce the length of the material (compression member) in the axis of the applied load, in other words the stress state caused by squeezing the material. A simple case of compression is the uniaxial compression induced by the action of opposite, pushing forces. Compressive strength for materials is generally higher than their tensile strength. However, structures loaded in compression are subject to additional failure modes dependent on geometry, such as buckling.

• Tensile stress is the stress state caused by an applied load that tends to elongate the material in the axis of the applied load, in other words the stress caused by pulling the material. The strength of structures of equal cross sectional area loaded in tension is independent of shape of the cross section. Materials loaded in tension are susceptible to stress concentrations such as material defects or abrupt changes in geometry. However, materials exhibiting ductile behavior (most metals for example) can tolerate some defects while brittle materials (such as ceramics) can fail well below their ultimate material strength.

• Shear stress is the stress state caused by a pair of the built energy by opposing forces acting along parallel lines of action through the material, in other words the stress caused by faces of the material sliding relative to one another. An example is cutting paper with scissors^[4] or stresses due to torsional loading.

Strength terms

• Yield strength is the lowest stress that produces a permanent deformation in a material. In some materials, like aluminium alloys, the point of yielding is difficult to identify, thus it is usually defined as the stress required to cause 0.002% plastic strain. This is called a 0.002% proof stress.^[5]

• Compressive strength is a limit state of compressive stress that leads to failure in the manner of ductile failure (infinite theoretical yield) or brittle failure (rupture as the result of crack propagation, or sliding along a weak plane - see shear strength).

• Tensile strength or ultimate tensile strength is a limit state of tensile stress that leads to tensile failure in the manner of ductile failure (yield as the first stage of that failure, some hardening in the second stage and breakage after a possible "neck" formation) or brittle failure (sudden breaking in two or more pieces at a low stress state). Tensile strength can be quoted as either true stress or engineering stress.

• Fatigue strength is a measure of the strength of a material or a component under cyclic loading,^[6] and is usually more difficult to assess than the static strength measures. Fatigue strength is quoted as stress amplitude or stress range (Δσ = σ_max − σ_min), usually at zero mean stress, along with the number of cycles to failure under that condition of stress.

• Impact strength, is the capability of the material to withstand a suddenly applied load and is expressed in terms of energy. Often measured with the Izod impact strength test or Charpy impact test, both of which measure the impact energy required to fracture a sample. Volume, modulus of elasticity, distribution of forces, and yield strength effect the impact strength of a material. In order for a material or object to have a higher impact strength the stresses must be distributed evenly throughout the object. It also must have a large volume with a low modulus of elasticity and a high material yield strength.^[7]

Strain (deformation) terms

• Deformation of the material is the change in geometry created when stress is applied (in the form of force loading, gravitational field, acceleration, thermal expansion, etc.). Deformation is expressed by the displacement field of the material.^[8]
• Strain or reduced deformation is a mathematical term that expresses the trend of the deformation change among the material field. Strain is the deformation per unit length.^[9] In the case of uniaxial loading - displacements of a specimen (for example a bar element) strain is expressed as the quotient of the displacement and the length of the specimen. For 3D displacement fields it is expressed as derivatives of displacement functions in terms of a second order tensor (with 6 independent elements).
• Deflection is a term to describe the magnitude to which a structural element bends under a load.^[10]

Stress-strain relations

Basic static response of a specimen under tension

• Elasticity is the ability of a material to return to its previous shape after stress is released. In many materials, the relation between applied stress is directly proportional to the resulting strain (up to a certain limit), and a graph representing those two quantities is a straight line.

The slope of this line is known as Young's Modulus, or the "Modulus of Elasticity." The Modulus of Elasticity can be used to determine the stress-strain relationship in the linear-elastic portion of the stress-strain curve. The linear-elastic region is either below the yield point, or if a yield point is not easily identified on the stress-strain plot it is defined to be between 0 and 0.2% strain, and is defined as the region of strain in which no yielding (permanent deformation) occurs.^[11]

• Plasticity or plastic deformation is the opposite of elastic deformation and is defined as unrecoverable strain. Plastic deformation is retained after the release of the applied stress. Most materials in the linear-elastic category are usually capable of plastic deformation. Brittle materials, like ceramics, do not experience any plastic deformation and will fracture under relatively low stress. Materials such as metals usually experience a small amount of plastic deformation before failure while ductile metals such as copper and lead or polymers will plasticly deform much more.

Consider the difference between a carrot and chewed bubble gum. The carrot will stretch very little before breaking. The chewed bubble gum, on the other hand, will plastically deform enormously before finally breaking.

Design terms

Ultimate strength is an attribute related to a material, rather than just a specific specimen made of the material, and as such it is quoted as the force per unit of cross section area (N/m²). The ultimate strength is the maximum stress that a material can withstand before it breaks or weakens.^[12] For example, the ultimate tensile strength (UTS) of AISI 1018 Steel is 440 MN/m². In general, the SI unit of stress is the pascal, where 1 Pa = 1 N/m². In Imperial units, the unit of stress is given as lbf/in² or pounds-force per square inch. This unit is often abbreviated as psi. One thousand psi is abbreviated ksi.

A Factor of safety is a design criteria that an engineered component or structure must achieve. FS = UTS / R, where FS: the factor of safety, R: The applied stress, and UTS: ultimate stress (psi or N/m^2) ^[13]

Margin of Safety is also sometimes used to as design criteria. It is defined MS = Failure Load/(Factor of Safety * Predicted Load) - 1

For example to achieve a factor of safety of 4, the allowable stress in an AISI 1018 steel component can be calculated to be R = UTS / FS = 440/4 = 110 MPa, or R = 110×10⁶ N/m². Such allowable stresses are also known as "design stresses" or "working stresses."

Design stresses that have been determined from the ultimate or yield point values of the materials give safe and reliable results only for the case of static loading. Many machine parts fail when subjected to a non steady and continuously varying loads even though the developed stresses are below the yield point. Such failures are called fatigue failure. The failure is by a fracture that appears to be brittle with little or no visible evidence of yielding. However, when the stress is kept below "fatigue stress" or "endurance limit stress", the part will endure indefinitely. A purely reversing or cyclic stress is one that alternates between equal positive and negative peak stresses during each cycle of operation. In a purely cyclic stress, the average stress is zero. When a part is subjected to a cyclic stress, also known as stress range (Sr), it has been observed that the failure of the part occurs after a number of stress reversals (N) even if the magnitude of the stress range is below the material’s yield strength. Generally, higher the range stress, the fewer the number of reversals needed for failure.

Failure theories

There are four important failure theories, namely (1) maximum shear stress theory, (2) maximum normal stress theory, (3) maximum strain energy theory, and (4) maximum distortion energy theory. Out of these four theories of failure, the maximum normal stress theory is only applicable for brittle materials, and the remaining three theories are applicable for ductile materials.

• Maximum Shear stress Theory- This theory postulates that failure will occur in a machine part if the magnitude of the maximum shear stress (tmax) in the part exceeds the shear strength (typ) of the material determined from uniaxial testing.

This theory postulates, that failure will occur when, tmax = typ or max of [|S1-S2|/2 , |S2-S3|/2 , and |S3-S1|/2] = Syp/2 Dividing both side by 2, max of [|S1-S2| , |S2-S3|, and |S3-S1|] = Syp Using a design factor of safety Nfs, the theory formulates the design equation as, max of [|S1-S2| , |S2-S3|, and |S3-S1|] should be less than or equal to Syp/Nfs

• Maximum normal stress theory- this theory postulates, that failure will occur in machine part if the maximum normal stress in the part exceeds the ultimate tensile stress of the material as determined from uniaxial testing. This theory deals with brittle materials only. The maximum tensile stress should be less than or equal to ultimate tensile stress divided by factor of safety. The magnitude of the maximum compressive stress should be less than ultimate compressive stress divided by factor of safety.

As the three principal stresses at a point in the part S1, S2, or S3 may be both tensile and compressive stresses, when this theory is applied, we need to check for failures both from tension and compression. The method of application of this theory is to find the maximum tensile stress, and the maximum compressive stress from the given values of S1, S2, and S3. The largest positive value among S1, S2, and S3 is the maximum tensile stress and the smallest negative value is the maximum compressive stress. For example if S1 = 80 MPa, S2 = -100 MPa, and S3 = -150 MPa, then the maximum tensile stress = 80 MPa, and the maximum compressive stress = -150 MPa (smallest negative value!).Thus according to this theory, the safe design condition for brittle material can be given by: The maximum tensile stress should be less than or equal to Sut/Nfs and The magnitude of the maximum compressive stress should less than Suc/Nfs

• Maximum strain energy theory-this theory postulates that failure will occur when the strain energy per unit volume due to the applied stresses in a part equals the strain energy per unit volume at the yield point in uniaxial testing.

Strain energy is the energy stored in a material due elastic deformation, which is, work done during elastic deformation. Work done per unit volume = strain x average stress. During tensile test, stress increases from zero to Syp, that is average stress = Syp/2.Elastic strain at yield point = Syp/E, where E is the elastic modulus of elasticity.Strain energy per unit volume during uniaxial tension = average stress x strain = Syp2/2E

• Maximum distortion energy theory- this theory is also known as shear energy theory or von Mises-Hencky theory. This theory postulates that failure will occur when the distortion energy per unit volume due to the applied stresses in a part equals the distortion energy per unit volume at the yield point in uniaxial testing. The total elastic energy due to strain can be divided into two parts. One part causes change in volume, and the other part causes change in shape. Distortion energy is the amount of energy that is needed to change the shape.

Application of failure theory

Out of the four theories, only the maximum normal stress theory predicts failure for brittle materials. The rest of the three theories are applicable for ductile materials. Out of these three, the distortion energy theory provides most accurate results in majority of the stress conditions.The strain energy theory needs the value of Poisson’s ratio of the part material, which is often not readily available. The maximum shear stress theory is conservative. For simple unidirectional normal stresses all theories are equivalent, which means all theories will give the same result.

See also

• Creep of materials
• Deformation-mechanism maps
• Diffusion in materials
• Dynamics
  • Thermodynamics
  • Fluid dynamics
• Elasticity of materials
• Fatigue of materials
• Forensic engineering
• Fracture mechanics
• Fracture toughness
• Heat transfer
• Materials science
• Material selection
• Microstructures of materials
• Plastics deformation in solids
• Plasticity of materials
• Schmidt hammer
• Specific strength
• Statics
• Stress concentration
• Strengthening mechanisms of materials

References

1. ^ Beer & Johnston (2006). Mechanics of Materials (5th ed.). McGraw Hill. pp. 210. ISBN 978-0-07-352938-7. 
2. ^ Beer & Johnston (2006). Mechanics of Materials (5th ed.). McGraw Hill. pp. 7. ISBN 978-0-07-352938-7. 
3. ^ Beer & Johnston (2006). Mechanics of Materials (5th ed.). McGraw Hill. pp. 5. ISBN 978-0-07-352938-7. 
4. ^ Beer & Johnston (2006). Mechanics of Materials (5th ed.). McGraw Hill. pp. 9–10. ISBN 978-0-07-352938-7. 
5. ^ Beer & Johnston (2006). Mechanics of Materials (5th ed.). McGraw Hill. pp. 52. ISBN 978-0-07-352938-7. 
6. ^ Beer & Johnston (2006). Mechanics of Materials (5th ed.). McGraw Hill. pp. 60. ISBN 978-0-07-352938-7. 
7. ^ Beer & Johnston (2006). Mechanics of Materials (5th ed.). McGraw Hill. pp. 693–696. ISBN 978-0-07-352938-7. 
8. ^ Beer & Johnston (2006). Mechanics of Materials (5th ed.). McGraw Hill. pp. 47. ISBN 978-0-07-352938-7. 
9. ^ Beer & Johnston (2006). Mechanics of Materials (5th ed.). McGraw Hill. pp. 49. ISBN 978-0-07-352938-7. 
10. ^ R. C. Hibbeler (2009). Structural Analysis (7th ed.). Pearson Prentice Hall. pp. 305. ISBN 978-0-13-602060-8. 
11. ^ Beer & Johnston (2006). Mechanics of Materials (5th ed.). McGraw Hill. pp. 53–56. ISBN 978-0-07-352938-7. 
12. ^ Beer & Johnston (2006). Mechanics of Materials (5th ed.). McGraw Hill. pp. 27–28. ISBN 978-0-07-352938-7. 
13. ^ Beer & Johnston (2006). Mechanics of Materials (5th ed.). McGraw Hill. pp. 28. ISBN 978-0-07-352938-7. 

Further reading

• Fa-Hwa Cheng, Initials. (1997). Strength of material. Ohio: McGraw-Hill
• Mechanics of Materials , E.J. Hearn
• Alfirević, Ivo. Strength of Materials I. Tehnička knjiga, 1995. ISBN 953-172-010-X.
• Alfirević, Ivo. Strength of Materials II. Tehnička knjiga, 1999. ISBN 953-6168-85-5.
• Ashby, M.F. Materials Selection in Design. Pergamon, 1992.
• Beer, F.P., E.R. Johnston, et al. Mechanics of Materials, 3rd edition. McGraw-Hill, 2001. ISBN 0-07-248673-2
• Cottrell, A.H. Mechanical Properties of Matter. Wiley, New York, 1964.
• Den Hartog, Jacob P. Strength of Materials. Dover Publications, Inc., 1961, ISBN 0-486-60755-0.
• Drucker, D.C. Introduction to Mechanics of Deformable Solids. McGraw-Hill, 1967.
• Gordon, J.E. The New Science of Strong Materials. Princeton, 1984.
• Groover, Mikell P. Fundamentals of Modern Manufacturing, 2nd edition. John Wiley & Sons,Inc., 2002. ISBN 0-471-40051-3.
• Hashemi, Javad and William F. Smith. Foundations of Materials Science and Engineering, 4th edition. McGraw-Hill, 2006. ISBN 007-125690-3.
• Hibbeler, R.C. Statics and Mechanics of Materials, SI Edition. Prentice-Hall, 2004. ISBN 013-129-011-8.
• Lebedev, Leonid P. and Michael J. Cloud. Approximating Perfection: A Mathematician's Journey into the World of Mechanics. Princeton University Press, 2004. ISBN 0-691-11726-8.
• Mott, Robert L. Applied Strength of Materials, 4th edition. Prentice-Hall, 2002. ISBN 0-13-088578-9.
• Popov, Egor P. Engineering Mechanics of Solids. Prentice Hall, Englewood Cliffs, N. J., 1990. ISBN 0-13-279258-3.
• Ramamrutham, S. Strength of Materials.
• Shames, I.H. and F.A. Cozzarelli. Elastic and inelastic stress analysis. Prentice-Hall, 1991. ISBN 1-56032-686-7.
• Timoshenko S. Strength of Materials, 3rd edition. Krieger Publishing Company, 1976, ISBN 0-88275-420-3.
• Timoshenko, S.P. and D.H. Young. Elements of Strength of Materials, 5th edition. (MKS System)
• Davidge, R.W., Mechanical Behavior of Ceramics, Cambridge Solid State Science Series, (1979)
• Lawn, B.R., Fracture of Brittle Solids, Cambridge Solid State Science Series, 2nd Edn. (1993)
• Green, D., An Introduction to the Mechanical Properties of Ceramics, Cambridge Solid State Science Series, Eds. Clarke, D.R., Suresh, S., Ward, I.M. (1998)

External links

• Failure theories
• case studies in structural failure