- Multilateration
-
Multilateration is a navigation technique based on the measurement of the difference in distance to two or more stations at known locations that broadcast signals at known times. Unlike measurements of absolute distance or angle, measuring the difference in distance results in an infinite number of locations that satisfy the measurement. When these possible locations are plotted, they form a hyperbolic curve. To locate the exact location along that curve, a second measurement is taken to a different pair of stations to produce a second curve, which intersects with the first. When the two are compared, a small number of possible locations are revealed, producing a "fix".
Multilateration is a common technique in radio navigation systems, where it is known as hyperbolic navigation. These systems are relatively easy to construct as there is no need for a common clock, and the difference in the signal timing can be measured visibly using an oscilloscope. This formed the basis of a number of widely used navigation systems starting in World War II with the British Gee system and several similar systems introduced over the next few decades. The introduction of the microprocessor greatly simplified operation, greatly increasing popularity during the 1980s. The most popular hyperbolic navigation system was LORAN-C, which was used around the world until the system was shut down in 2010. Other systems continue to be used, but the widespread use of satellite navigation systems like GPS have made these systems largely redundant.
Multilateration should not be confused with trilateration, which uses distances or absolute measurements of time-of-flight from three or more sites, or with triangulation, which uses the measurement of absolute angles. Both of these systems are also commonly used with radio navigation systems; trilateration is the basis of GPS.
Contents
Principle
Multilateration is commonly used in civil and military surveillance applications to accurately locate an aircraft, vehicle or stationary emitter by measuring the "Time Difference of Arrival" (TDOA) of a signal from the emitter at three or more receiver sites.
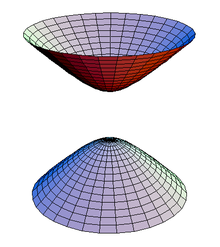
If a pulse is emitted from a platform, it will arrive at slightly different times at two spatially separated receiver sites, the TDOA being due to the different distances of each receiver from the platform. In fact, for given locations of the two receivers, a whole set of emitter locations would give the same measurement of TDOA. Given two receiver locations and a known TDOA, the locus of possible emitter locations is a one half of a two-sheeted hyperboloid.
In simple terms, with two receivers at known locations, an emitter can be located onto a hyperboloid[1]. Note that the receivers do not need to know the absolute time at which the pulse was transmitted – only the time difference is needed.
Consider now a third receiver at a third location. This would provide a second TDOA measurement and hence locate the emitter on a second hyperboloid. The intersection of these two hyperboloids describes a curve on which the emitter lies.
If a fourth receiver is now introduced, a third TDOA measurement is available and the intersection of the resulting third hyperboloid with the curve already found with the other three receivers defines a unique point in space. The emitter's location is therefore fully determined in 3D.
In practice, errors in the measurement of the time of arrival of pulses mean that enhanced accuracy can be obtained with more than four receivers. In general, N receivers provide N − 1 hyperboloids. When there are N > 4 receivers, the N − 1 hyperboloids should, assuming a perfect model and measurements, intersect on a single point. In reality, the surfaces rarely intersect, because of various errors. In this case, the location problem can be posed as an optimization problem and solved using, for example, a least squares method or an extended Kalman filter.
Additionally, the TDOA of multiple transmitted pulses from the emitter can be averaged to improve accuracy.
Reciprocal case: locating a receiver from multiple transmitter sites
Multilateration can also be used by a single receiver to locate itself, by measuring the TDOA of signals emitted from three or more synchronised transmitters at known locations. This can be used by navigation systems, an example being the British DECCA navigation system, developed during World War II, which used the phase-difference of two transmitters, rather than the TDOA of a pulse, to define the hyperboloids. This allowed the transmitters to broadcast a continuous wave signal. Phase-difference and time-difference can be considered the same for narrow-band transmitters.
TDOA geometry
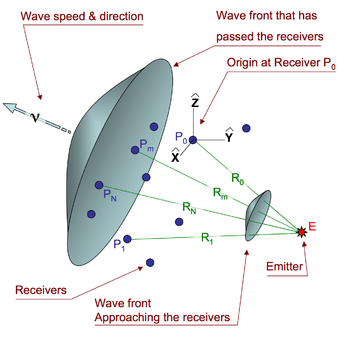
Consider an emitter (E in Figure 2) at an unknown location vector
- E = (x, y, z)
which we wish to locate. The source is within range of N+1 receivers at known locations
- P0, P1, ..., Pm, ..., PN.
The subscript m refers to any one of the receivers:
- Pm = (xm, ym, zm)
- 0 ≤ m ≤ N
The distance (R) from the emitter to one of the receivers in terms of the coordinates is
-

(
The math is made easier by placing the origin at one of the receivers (P0), which makes its distance to the emitter
-

(
Measuring the Time Difference in a TDOA System
The distance Rm in equation 1 is the wave speed (v) times transit time (Tm). A TDOA multilateration system measures the time difference (τm) of a wavefront touching each receiver. The TDOA equation for receivers m and 0 is
-

(
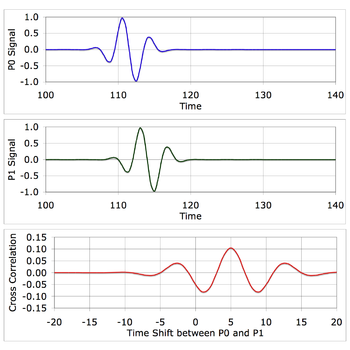
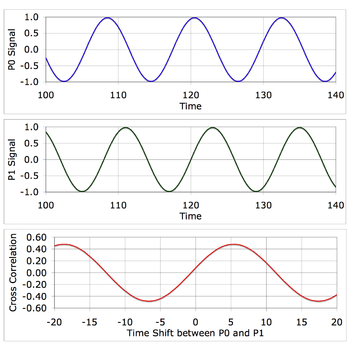
Figure 3a is a simulation of the a pulse waveform recorded by receivers P0 and P1. The spacing between E, P1 and P0 is such that the pulse takes 5 time units longer to reach P1 than P0. The units of time in Figure 3 are arbitrary. The following table gives approximate time scale units for recording different types of waves.
Type of wave Material Time Units Acoustic Air 1 millisecond Acoustic Water 1/2 millisecond Acoustic Rock 1/10 millisecond Electromagnetic Vacuum, air 1 nanosecond The red curve in Figure 3a is the cross-correlation function
 . The cross correlation function slides one curve in time across the other and returns a peak value when the curve shapes match. The peak at time = 5 is a measure of the time shift between the recorded waveforms, which is also the τ value needed for Equation 3.
. The cross correlation function slides one curve in time across the other and returns a peak value when the curve shapes match. The peak at time = 5 is a measure of the time shift between the recorded waveforms, which is also the τ value needed for Equation 3.Figure 3b is the same type of simulation for a wide-band waveform from the emitter. The time shift is 5 time units because the geometry and wave speed is the same as the Figure 3a example. Again, the peak in the cross correlation occurs at τ1 = 5.
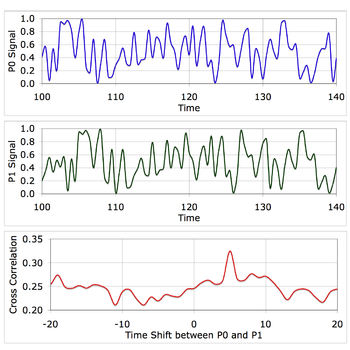
Figure 3c is an example of a continuous, narrow-band waveform from the emitter. The cross correlation function shows an important factor when choosing the receiver geometry. There is a peak at Time = 5 plus every increment of the waveform period. To get one solution for the measured time difference, the largest space between any two receivers must be closer than one wavelength of the emitter signal. Some systems, such as the LORAN C and Decca mentioned at earlier (recall the same math works for moving receiver & multiple known transmitters), use spacing larger than 1 wavelength and include equipment, such as a Phase Detector, to count the number of cycles that pass by as the emitter moves. This only works for continuous, narrow-band waveforms because of the relation between phase (θ), frequency (f) and time (T)
 .
.
The phase detector will see variations in frequency as measured phase noise, which will be an uncertainty that propagates into the calculated location. If the phase noise is large enough, the phase detector can become unstable.
3-D Solution
Equation 3 is the hyperboloid described in the previous section, where 4 receivers (0 ≤ m ≤ 3) lead to 3 non-linear equations in 3 unknown values (x,y,z). The system must then solve for the unknown emitter location in real time.
Civilian air traffic control multilateration systems use the Mode C SSR transponder return to find the altitude (z). Three or more receivers at known locations are used to find the other 2 dimensions (x, y).
R. Bucher and D. Misra show the detailed algebra to locate 1 receiver with TDOA between 3 transmitters.[2] Their solution is a set of linear equations to find (x, y) and a quadratic for (z).
Improving accuracy with a large number of receivers can be a problem for devices with small embedded processors because of the time required to solve several simultaneous, non-linear equations (1, 2 & 3). The TDOA problem can be turned into a system of linear equations when there are 5 or more receivers, which can reduce the computation time. Starting with equation 3, solve for Rm, square both sides, collect terms and divide all terms by vτm:
-

(
Removing the 2 R0 term will eliminate all the square root terms. That is done by subtracting the TDOA equation of receiver m = 1 from each of the others (2 ≤ m ≤ N)
-

(
Focus for a moment on equation 1. Square Rm, group similar terms and use equation 2 to replace some of the terms with R0.
-

(
Combine equations 5 and 6, and write as a set of linear equations of the unknown emitter location x,y,z
-

(
Use equation 7 to generate the four constants Am,Bm,Cm,Dm from measured distances and time for each receiver 2 ≤ m ≤ N. This will be a set of N homogeneous linear equations.
There are many robust linear algebra methods that can solve for the values of (x,y,z), such as Singular value decomposition or Gaussian Elimination. Chapter 15 in Numerical Recipes [3] describes several methods to solve linear equations and estimate the uncertainty of the resulting values.
2-D Solution
Finding the emitter location in a two dimensional geometry can use any of the methods used for the 3-D geometry. The coordinate frame is typically defined to make the z dimension zero or constant. Examples of 2-D multilateration are short wave radio long distance communications through the Earth's atmosphere, acoustic wave propagation in the sound fixing and ranging channel of the oceans and the LORAN navigation system.
Accuracy
For trilateration or multilateration, calculation is done based on distances, which requires the frequency and the wave count of a received transmission. For triangulation or multiangulation, calculation is done based on angles, which requires the phases of received transmission plus the wave count.
For lateration compared to angulation, the numerical problems compare, but the technical problem is more challenging with angular measurements, as angles require two measures per position when using optical or electronic means for measuring phase differences instead of counting wave cycles.
Trilateration in general is calculating with triangles of known distances/sizes, mathematically a very sound system. In a triangle, the angles can be derived if one knows the length of all sides, (see congruence), but the length of the sides cannot be derived based on all of the angles, not without knowing the length of at least one of the sides (a baseline) (see similarity).
In 3D, when four or more angles are in play, locations can be calculated from n + 1 = 4 measured angles plus one known baseline or from just n + 1 = 4 measured sides.
Multilateration is, in general, far more accurate for locating an object than sparse approaches such as trilateration, where with planar problems just three distances are known and computed. Multilateration serves for several aspects:
- over-determination of an n-variable quadratic problem with (n + 1) + m quadratic equations
- stochastic errors prohibiting a deterministic approach to solving the equations
- clustering needs to segregate members of various clusters contributing to various models of solving, i.e. fixed locations, oscillating locations and moving locations
Accuracy of multilateration is a function of several variables, including:
- The antenna or sensor geometry of the receiver(s) and transmitter(s) for electronic or optical transmission.
- The timing accuracy of the receiver system, i.e. thermal stability of the clocking oscillators.
- The accuracy of frequency synchronisation of the transmitter oscillators with the receiver oscillators.
- Phase synchronisation of the transmitted signal with the received signal, as propagation effects as e.g. diffraction or reflection changes the phase of the signal thus indication deviation from line of sight, i.e. multipath reflections.
- The bandwidth of the emitted pulse(s) and thus the rise-time of the pulses with pulse coded signals in transmission.
- Inaccuracies in the locations of the transmitters or receivers when used as a known location
The accuracy can be calculated by using the Cramér–Rao bound and taking account of the above factors in its formulation.
Example applications
- Sound ranging – Using sound to locate artillery fire.
- Decca Navigator System – A system used from the end of World War II to the year 2000, employing the phase-difference of multiple transmitters to locate on the intersection of hyperboloids
- OMEGA Navigation System – A worldwide system similar to Decca, shut down in 1997
- GEE – British aircraft location technique from World War II, using accurate reference transmitters
- LORAN-C – navigation system using TDOA of signals from multiple synchronised transmitters
- Passive ESM multilateration systems, including Kopáč, Ramona, Tamara, VERA and possibly Kolchuga – location of a transmitter using multiple receivers
- Mobile phone tracking – using multiple base stations to estimate phone location (by either the phone itself, or the phone network)
- Reduced Vertical Separation Minima (RVSM) monitoring using Secondary Surveillance Radar – Mode C/S transponder replies to calculate the position of an aircraft. Application to RVSM was first demonstrated by Roke Manor Research Limited in 1992.[citation needed]
Simplification
For applications where no need for absolute coordinates determination is assessed, the implementing of a more simple solution is advantageous. Compared to multilateration as the concept of crisp locating, the other option is fuzzy locating, where just one distance delivers the relation between detector and detected object. This most simple approach is unilateration. However, such unilateration approach never delivers the angular position with reference to the detector. Many solutions are available today [4][5][6][7][8]. Some of these vendors offer a position estimate based on combining several laterations. This approach is often not stable, when the wireless ambience is affected by metal or water masses. Other vendors offer room discrimination with a room-wise excitation, one vendor offers a position discrimination with a contiguity excitation.
See also
- FDOA Frequency difference of arrival. Analogous to TDOA using differential doppler.
- Triangulation – Location by angular measurement on lines of bearing that intersect
- Trilateration – Location by distance (e.g. time-of-flight) measurement on coincident signals from multiple transmitters.
- Mobile phone tracking – used in GSM networks
- Multidimensional scaling
- Radiolocation
- Radio navigation
- Real-time locating – International standard for asset and staff tracking using wireless hardware and real-time software
- Real time location system – General techniques for asset and staff tracking using wireless hardware and real-time software
References
- The Multilateration Executive Reference Guide is an easy-to-read reference for air traffic management, airport and airline professionals to learn more about this next-generation surveillance technology
Notes
- ^ In other words, given two receivers at known locations, one can derive a three-dimensional surface (characterized as one half of a hyperboloid) for which any two points on said surface will have the same differential distance from said receivers, i.e., a signal transmitted from any point on the surface will have the same TDOA (measured by the receivers) as a signal transmitted from any other point on the surface.
Therefore, in practice, the TDOA corresponding to a (moving) transmitter is measured, a corresponding hyperbolic surface is derived, and the transmitter is said to be "located" somewhere on the that surface. - ^ A Synthesizable VHDL Model of the Exact Solution for Three-dimensional Hyperbolic Positioning System, Ralph Bucher and D. Misra, VLSI Design, Volume 15 (2002), Issue 2, Pages 507-520.
- ^ Numerical Recipes official website
- ^ Sonitor Technologies, NO-0314 Oslo, Norway: SONITOR Ultra sound proprietary approach
- ^ RF Code, Austin, TX 78758, USA: RF Code 433 MHz proprietary approach
- ^ ReadPost Bremerhaven Germany: TokLoc®, the Bluetooth® LowEnergy based approach
- ^ Albis Zurich Switzerland: ZOMOFI Microwave proprietary approach
- ^ Location estimation in wireless telecommunication networks: Ekahau proprietary modified WLAN fuzzy locating approach
Categories:- Elementary geometry
- Euclidean geometry
- Radio navigation
- Geolocation
- Ubiquitous computing
- Wireless locating
Wikimedia Foundation. 2010.