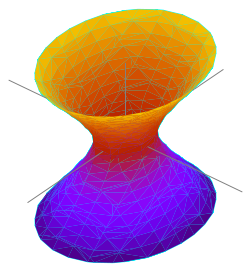
- Hyperboloid
-
Not to be confused with Hyperbolic paraboloid.
In mathematics, a hyperboloid is a quadric – a type of surface in three dimensions – described by the equation
 (hyperboloid of one sheet),
(hyperboloid of one sheet),
or
 (hyperboloid of two sheets).
(hyperboloid of two sheets).
These are also called elliptical hyperboloids. If and only if a = b, it is a hyperboloid of revolution, and is also called a circular hyperboloid.
Contents
Properties
A hyperboloid of revolution of one sheet can be obtained by revolving a hyperbola around its semi-minor axis. Alternatively, a hyperboloid of two sheets of axis AB is obtained as the set of points P such that AP−BP is a constant, AP being the distance between A and P. Points A and B are then called the foci of the hyperboloid. A hyperboloid of revolution of two sheets can be obtained by revolving a hyperbola around its semi-major axis.
A hyperboloid of one sheet is a doubly ruled surface; if it is a hyperboloid of revolution, it can also be obtained by revolving a line about a skew line.
Whereas the Gaussian curvature of a hyperboloid of one sheet is negative, that of a two-sheet hyperboloid is positive. In spite of its positive curvature, the hyperboloid of two sheets with another suitably chosen metric can also be used as a model for hyperbolic geometry.
Degenerate
A degenerate hyperboloid is of the form
if a = b then this will give a cone, if not then it gives an elliptical cone.
In more than three dimensions
Imaginary hyperboloids are frequently found in mathematics of higher dimensions. For example, in a pseudo-Euclidean space one has the use of a quadratic form:
When c is any constant, then the part of the space given by
is called a hyperboloid. The degenerate case corresponds to c = 0.
As an example, consider the following passage from Hawkins (2000):
- ...the velocity vectors always lie on a surface which Minkowski calls a four-dimensional hyperboloid since, expressed in terms of purely real coordinates (y1,...y4), its equation is
 analogous to the hyperboloid
analogous to the hyperboloid  of three-dimensional space.
of three-dimensional space.
However, the term quasi-sphere is also used in this context since the sphere and hyperboloid have some commonality (See the section "Relation to the sphere" below).
Hyperboloid structures
Main article: Hyperboloid structureOne-sheeted hyperboloids are used in construction, with the structures called hyperboloid structures. A hyperboloid is a doubly ruled surface so can be built with straight steel beams, producing a strong structure more cheaply than other methods. Examples include cooling towers, especially of power stations, and many other structures.
Relation to the sphere
In 1853 William Rowan Hamilton published his Lectures on Quaternions which included presentation of biquaternions. The following passage from page 673 shows how Hamilton uses biquaternion algebra and vectors from quaternions to produce hyperboloids from the equation of a sphere:
- ...the equation of the unit sphere ρ2 + 1 = 0, and change the vector ρ to a bivector form, such as σ + τ
 . The equation of the sphere then breaks up into the system of the two following,
. The equation of the sphere then breaks up into the system of the two following,
- σ2 − τ2 + 1 = 0, S.στ = 0;
- and suggests our considering σ and τ as two real and rectangular vectors, such that
- Tτ = (Tσ2 − 1 )½.
- Hence it is easy to infer that if we assume σ
 λ, where λ is a vector in a given position, the new real vector σ + τ will terminate on the surface of a double-sheeted and equilateral hyperboloid; and that if, on the other hand, we assume τ
λ, where λ is a vector in a given position, the new real vector σ + τ will terminate on the surface of a double-sheeted and equilateral hyperboloid; and that if, on the other hand, we assume τ  λ, then the locus of the extremity of the real vector σ + τ will be an equilateral but single-sheeted hyperboloid. The study of these two hyperboloids is, therefore, in this way connected very simply, through biquaternions, with the study of the sphere;...
λ, then the locus of the extremity of the real vector σ + τ will be an equilateral but single-sheeted hyperboloid. The study of these two hyperboloids is, therefore, in this way connected very simply, through biquaternions, with the study of the sphere;...
In this passage S is the operator giving the scalar part of a quaternion, and T is the "tensor", now called norm, of a quaternion.
A modern view of the unification of the sphere and hyperboloid uses the idea of a conic section as a slice of a quadratic form. Instead of a conical surface, one requires conical hypersurfaces in four-dimensional space with points
 determined by quadratic forms. First consider the conical hypersurface
determined by quadratic forms. First consider the conical hypersurface and
and which is a hyperplane.
which is a hyperplane.
Then
 is the sphere with radius r . On the other hand, the conical hypersurface
is the sphere with radius r . On the other hand, the conical hypersurface provides that
provides that  is a hyperboloid.
is a hyperboloid.
In the theory of quadratic forms, a unit quasi-sphere is the subset of a quadratic space X consisting of the x ∈ X such that the quadratic norm of x is one. See Porteous (1995) where this term includes both hyperboloid and sphere.
See also
- Hyperbola
- Ellipsoid
- Paraboloid / Hyperbolic paraboloid
- Hyperboloid structure
- Ruled surface
- de Sitter space
- Vladimir Shukhov
References
- Wilhelm Blaschke (1948) Analytische Geometrie,Kapital V: "Quadriken", Wolfenbutteler Verlagsanstalt.
- David A. Brannan, M. F. Esplen, & Jeremy J Gray (1999) Geometry, pages 39–41 Cambridge University Press.
- H. S. M. Coxeter (1961) Introduction to Geometry, page 130, John Wiley & Sons.
- Thomas Hawkins (2000) Emergence of the Theory of Lie Groups: an essay in the history of mathematics, 1869 — 1926, §9.3 "The Mathematization of Physics at Göttingen", see page 340, Springer ISBN 0387989633.
- Ian R. Porteous (1995) Clifford Algebras and the Classical Groups, pages 22,24, & 106, Cambridge University Press ISBN 0521551773.
External links
Categories:- Geometric shapes
- Surfaces
- Quadrics
Wikimedia Foundation. 2010.