Product rule

For Euler's chain rule relating partial derivatives of three independent variables, see Triple product rule.

For the counting principle in combinatorics, see Rule of product.

Topics in Calculus

Fundamental theorem Limits of functions Continuity Mean value theorem Differential calculus  Derivative Change of variables Implicit differentiation Taylor's theorem Related rates Rules and identities: Power rule, Product rule, Quotient rule, Chain rule Integral calculus  Integral Lists of integrals Improper integrals Integration by: parts, disks, cylindrical shells, substitution, trigonometric substitution, partial fractions, changing order Vector calculus  Gradient Divergence Curl Laplacian Gradient theorem Green's theorem Stokes' theorem Divergence theorem Multivariable calculus  Matrix calculus Partial derivative Multiple integral Line integral Surface integral Volume integral Jacobian

In calculus, the product rule is a formula used to find the derivatives of products of two or more functions. It may be stated thus:

$(f\cdot g)'=f'\cdot g+f\cdot g' \,\!$

or in the Leibniz notation thus:

$\dfrac{d}{dx}(u\cdot v)=u\cdot \dfrac{dv}{dx}+v\cdot \dfrac{du}{dx}$.

The derivative of the product of three functions is:

$\dfrac{d}{dx}(u\cdot v \cdot w)=\dfrac{du}{dx} \cdot v \cdot w + u \cdot \dfrac{dv}{dx} \cdot w + u\cdot v\cdot \dfrac{dw}{dx}$.

Discovery by Leibniz

Discovery of this rule is credited to Gottfried Leibniz (however, Child (2008) argues that it is due to Isaac Barrow), who demonstrated it using differentials. Here is Leibniz's argument: Let u(x) and v(x) be two differentiable functions of x. Then the differential of uv is

$\begin{align} d(u\cdot v) & {} = (u + du)\cdot (v + dv) - u\cdot v \\ & {} = u\cdot dv + v\cdot du + du\cdot dv. \end{align}$

Since the term du·dv is "negligible" (compared to du and dv), Leibniz concluded that

$d(u\cdot v) = v\cdot du + u\cdot dv \,\!$

and this is indeed the differential form of the product rule. If we divide through by the differential dx, we obtain

$\frac{d}{dx} (u\cdot v) = v \cdot \frac{du}{dx} + u \cdot \frac{dv}{dx} \,\!$

which can also be written in "prime notation" as

$(u\cdot v)' = v\cdot u' + u\cdot v'. \,\!$

Examples

• Suppose we want to differentiate ƒ(x) = x² sin(x). By using the product rule, one gets the derivative ƒ '(x) = 2x sin(x) + x²cos(x) (since the derivative of x² is 2x and the derivative of sin(x) is cos(x)).
• One special case of the product rule is the constant multiple rule which states: if c is a real number and ƒ(x) is a differentiable function, then cƒ(x) is also differentiable, and its derivative is (c × ƒ)'(x) = c × ƒ '(x). This follows from the product rule since the derivative of any constant is zero. This, combined with the sum rule for derivatives, shows that differentiation is linear.
• The rule for integration by parts is derived from the product rule, as is (a weak version of) the quotient rule. (It is a "weak" version in that it does not prove that the quotient is differentiable, but only says what its derivative is if it is differentiable.)

A common error

It is a common error, when studying calculus, to suppose that the derivative of (uv) equals (u ′)(v ′). Leibniz himself made this error initially;^[1] however, there are clear counterexamples. Consider a differentiable function ƒ(x) whose derivative is ƒ '(x). This function can also be written as ƒ(x) · 1, since 1 is the identity element for multiplication. If the above-mentioned misconception were true, (u′)(v′) would equal zero. This is true because the derivative of a constant (such as 1) is zero and the product of ƒ '(x) · 0 is also zero.

Proof of the product rule

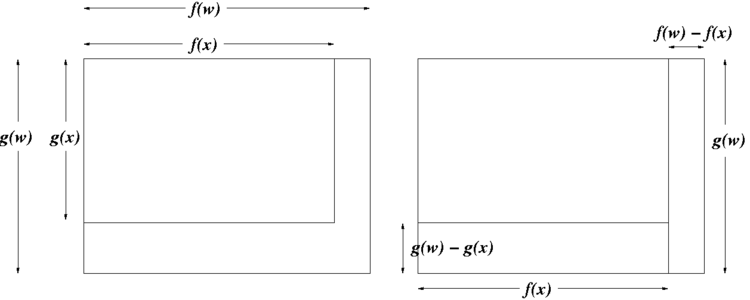
A rigorous proof of the product rule can be given using the properties of limits and the definition of the derivative as a limit of Newton's difference quotient.

If

$h(x) = f(x)g(x),\,$

and ƒ and g are each differentiable at the fixed number x, then

$h'(x) = \lim_{w\to x}{ h(w) - h(x) \over w - x} = \lim_{w\to x}{f(w)g(w) - f(x)g(x) \over w - x}. \qquad\qquad(1)$

Now the difference

$f(w)g(w) - f(x)g(x)\qquad\qquad(2)$

is the area of the big rectangle minus the area of the small rectangle in the illustration.

The region between the smaller and larger rectangle can be split into two rectangles, the sum of whose areas is^[2]

$f(x) \Bigg( g(w) - g(x) \Bigg) + g(w)\Bigg( f(w) - f(x) \Bigg).\qquad\qquad(3)$

Therefore the expression in (1) is equal to

$\lim_{w\to x}\left( f(x) \left( {g(w) - g(x) \over w - x} \right) + g(w)\left( {f(w) - f(x) \over w - x} \right) \right).\qquad\qquad(4)$

Assuming that all limits used exist, (4) is equal to

$\left(\lim_{w\to x}f(x)\right) \left(\lim_{w\to x} {g(w) - g(x) \over w - x}\right) + \left(\lim_{w\to x} g(w)\right) \left(\lim_{w\to x} {f(w) - f(x) \over w - x} \right). \qquad\qquad(5)$

Now

$\lim_{w\to x}f(x) = f(x)$

This holds because f(x) remains constant as w → x.

$\lim_{w\to x} g(w) = g(x)\,$

This holds because differentiable functions are continuous (g is assumed differentiable in the statement of the product rule).

Also:

$\lim_{w\to x} {f(w) - f(x) \over w - x} = f'(x)$    and    $\lim_{w\to x} {g(w) - g(x) \over w - x} = g'(x)$

because f and g are differentiable at x;

We conclude that the expression in (5) is equal to

$f(x)g'(x) + g(x)f'(x). \,$

Alternative proofs

A Brief Proof

By definition, if $f, g: \mathbb{R} \rightarrow \mathbb{R}$ are differentiable at x₀ then we can write

$f(x+h) = f(x) + f'(x)h + \psi_1(h) \qquad \qquad g(x+h) = g(x) + g'(x)h + \psi_2(h)$

such that $\lim_{h \to 0} \frac{\psi_1(h)}{h} = \lim_{h \to 0} \frac{\psi_2(h)}{h} = 0$, that is, ψ₁,ψ₂∼O(h). Then:

$\begin{align} fg(x+h) - fg(x) = (f(x) + f'(x)h +\psi_1(h))(g(x) + g'(x)h + \psi_2(h)) - fg(x)= f'(x)g(x)h + f(x)g'(x)h + O(h) \\[12pt] \end{align}$

Taking the limit for small h gives the result.

Using logarithms

Let f = uv and suppose u and v are positive functions of x. Then

$\ln f =\ln (u\cdot v)=\ln u + \ln v.\,$

Differentiating both sides:

${1 \over f} {df \over dx} = {1 \over u} {du \over dx} + {1 \over v} {dv \over dx}\,$

and so, multiplying the left side by f, and the right side by uv,

${df \over dx} = v {du \over dx} + u {dv \over dx}.\,$

The proof appears in [1]. Note that since u, v need to be continuous, the assumption on positivity does not diminish the generality.

This proof relies on the chain rule and on the properties of the natural logarithm function, both of which are deeper than the product rule. From one point of view, that is a disadvantage of this proof. On the other hand, the simplicity of the algebra in this proof perhaps makes it easier to understand than a proof using the definition of differentiation directly.

Using the chain rule

The product rule can be considered a special case of the chain rule for several variables.

${d (ab) \over dx} = \frac{\partial(ab)}{\partial a}\frac{da}{dx}+\frac{\partial (ab)}{\partial b}\frac{db}{dx} = b \frac{da}{dx} + a \frac{db}{dx}. \,$

Using non-standard analysis

Let u and v be continuous functions in x, and let dx, du and dv be infinitesimals within the framework of non-standard analysis, specifically the hyperreal numbers. Using st to denote the standard part function that associates to a finite hyperreal number the real infinitely close to it, this gives

$\frac{d(uv)}{dx}\,$	$=\operatorname{st}\left(\frac{(u + \mathrm du)(v + \mathrm dv) - uv}{\mathrm dx}\right)$
	$=\operatorname{st}\left(\frac{uv + u \cdot \mathrm dv + v \cdot \mathrm du + \mathrm dv \cdot \mathrm du -uv}{\mathrm dx}\right)$
	$=\operatorname{st}\left(\frac{u \cdot \mathrm dv + (v + \mathrm dv) \cdot \mathrm du}{\mathrm dx}\right)$
	$={u}\frac{dv}{dx} + {v}\frac{du}{dx}$

Using smooth infinitesimal analysis

In the context of Lawvere's approach to infinitesimals, let du and dv be nilsquare infinitesimals. Then

$\begin{align} d(uv) & {} = (u + du)(v + dv) -uv \\ & {} = uv + u\cdot dv + v\cdot du + du\cdot dv - uv \\ & {} = u\cdot dv + v\cdot du + du\cdot dv \\ & {} = u\cdot dv + v\cdot du\,\! \end{align}$

provided that

$du \cdot dv = 0\,\!$

(this may not actually be true even for nilsquare infinitesimals in general).

Generalizations

A product of more than two factors

The product rule can be generalized to products of more than two factors. For example, for three factors we have

$\frac{d(uvw)}{dx} = \frac{du}{dx}vw + u\frac{dv}{dx}w + uv\frac{dw}{dx}\,\!$.

For a collection of functions $f_1, \dots, f_k$, we have

$\frac{d}{dx} \left [ \prod_{i=1}^k f_i(x) \right ] = \sum_{i=1}^k \left(\frac{d}{dx} f_i(x) \prod_{j\ne i} f_j(x) \right) = \left( \prod_{i=1}^k f_i(x) \right) \left( \sum_{i=1}^k \frac{f'_i(x)}{f_i(x)} \right).$

Higher derivatives

It can also be generalized to the Leibniz rule for the nth derivative of a product of two factors:

$(uv)^{(n)}(x) = \sum_{k=0}^n {n \choose k} \cdot u^{(n-k)}(x)\cdot v^{(k)}(x).$

See also binomial coefficient and the formally quite similar binomial theorem. See also Leibniz rule (generalized product rule).

Higher partial derivatives

For partial derivatives, we have

${\partial^n \over \partial x_1\,\cdots\,\partial x_n} (uv) = \sum_S {\partial^{|S|} u \over \prod_{i\in S} \partial x_i} \cdot {\partial^{n-|S|} v \over \prod_{i\not\in S} \partial x_i}$

where the index S runs through the whole list of 2ⁿ subsets of {1, ..., n}. For example, when n = 3, then

$\begin{align} &{}\quad {\partial^3 \over \partial x_1\,\partial x_2\,\partial x_3} (uv) \\ \\ &{}= u \cdot{\partial^3 v \over \partial x_1\,\partial x_2\,\partial x_3} + {\partial u \over \partial x_1}\cdot{\partial^2 v \over \partial x_2\,\partial x_3} + {\partial u \over \partial x_2}\cdot{\partial^2 v \over \partial x_1\,\partial x_3} + {\partial u \over \partial x_3}\cdot{\partial^2 v \over \partial x_1\,\partial x_2} \\ \\ &{}\qquad + {\partial^2 u \over \partial x_1\,\partial x_2}\cdot{\partial v \over \partial x_3} + {\partial^2 u \over \partial x_1\,\partial x_3}\cdot{\partial v \over \partial x_2} + {\partial^2 u \over \partial x_2\,\partial x_3}\cdot{\partial v \over \partial x_1} + {\partial^3 u \over \partial x_1\,\partial x_2\,\partial x_3}\cdot v. \end{align}$

A product rule in Banach spaces

Suppose X, Y, and Z are Banach spaces (which includes Euclidean space) and B : X × Y → Z is a continuous bilinear operator. Then B is differentiable, and its derivative at the point (x,y) in X × Y is the linear map D_(x,y)B : X × Y → Z given by

$(D_\left( x,y \right)\,B)\left( u,v \right) = B\left( u,y \right) + B\left( x,v \right)\qquad\forall (u,v)\in X \times Y.$

Derivations in abstract algebra

In abstract algebra, the product rule is used to define what is called a derivation, not vice versa.

For vector functions

The product rule extends to scalar multiplication, dot products, and cross products of vector functions.

For scalar multiplication: $(f \cdot \vec g)' = f\;'\cdot \vec g + f \cdot \vec g\;' \,$

For dot products: $(\vec f \cdot \vec g)' = \vec f\;'\cdot \vec g + \vec f \cdot \vec g\;' \,$

For cross products: $(\vec f \times \vec g)' = \vec f\;' \times \vec g + \vec f \times \vec g\;' \,$

(Beware: since cross products are not commutative, it is not correct to write $(f\times g)'=f'\times g+g'\times f. \,$ But cross products are anticommutative, so it can be written as $(f\times g)'=f'\times g-g'\times f. \,$

For scalar fields

For scalar fields the concept of gradient is the analog of the derivative:

$\nabla (f \cdot g) = \nabla f \cdot g + f \cdot \nabla g \,$

An application

Among the applications of the product rule is a proof that

${d \over dx} x^n = nx^{n-1}\,\!$

when n is a positive integer (this rule is true even if n is not positive or is not an integer, but the proof of that must rely on other methods). The proof is by mathematical induction on the exponent n. If n = 0 then xⁿ is constant and nx^n − 1 = 0. The rule holds in that case because the derivative of a constant function is 0. If the rule holds for any particular exponent n, then for the next value, n + 1, we have

$\begin{align} {d \over dx}x^{n+1} &{}= {d \over dx}\left( x^n\cdot x\right) \\[12pt] &{}= x{d \over dx} x^n + x^n{d \over dx}x \qquad\mbox{(the product rule is used here)} \\[12pt] &{}= x\left(nx^{n-1}\right) + x^n\cdot 1\qquad\mbox{(the induction hypothesis is used here)} \\[12pt] &{}= (n + 1)x^n. \end{align}$

Therefore if the proposition is true of n, it is true also of n + 1.

See also

• General Leibniz rule
• Reciprocal rule
• Differential (calculus)
• Derivation (abstract algebra)
• Product Rule Practice Problems [Kouba, University of California: Davis]

References

1. ^ Michelle Cirillo (August 2007). "Humanizing Calculus". The Mathematics Teacher 101 (1): 23–27. http://www.nctm.org/uploadedFiles/Articles_and_Journals/Mathematics_Teacher/Humanizing%20Calculus.pdf. 
2. ^ The illustration disagrees with some special cases, since – in actuality – ƒ(w) need not be greater than ƒ(x) and g(w) need not be greater than g(x). Nonetheless, the equality of (2) and (3) is easily checked by algebra.

• Child, J. M. (2008) "The early mathematical manuscripts of Leibniz", Gottfried Wilhelm Leibniz, translated by J. M. Child; page 29, footnote 58.