- Heptellated 8-simplex
-

8-simplex















Heptellated 8-simplex














Heptihexipentisteriruncicantitruncated 8-simplex
(Omnitruncated 8-simplex)















Orthogonal projections in A8 Coxeter plane (A7 for omnitruncation) In eight-dimensional geometry, a heptellated 8-simplex is a convex uniform 8-polytope, including 7th-order truncations (heptellation) from the regular 8-simplex.
There are 35 unique heptellations for the 8-simplex, including all permutations of truncations, cantellations, runcinations, sterications, and pentellations. The simplest heptellated 8-simplex is also called an expanded 8-simplex, with only the first and last nodes ringed, is constructed by an expansion operation applied to the regular 8-simplex. The highest form, the heptihexipentisteriruncicantitruncated 8-simplex is more simply called a omnitruncated 8-simplex with all of the nodes ringed.
Contents
Heptellated 8-simplex
Heptellated 8-simplex Type uniform polyzetton Schläfli symbol t0,7{3,3,3,3,3,3,3} Coxeter-Dynkin diagrams 














7-faces 6-faces 5-faces 4-faces Cells Faces Edges 504 Vertices 72 Vertex figure 6-simplex antiprism Coxeter group A8, [[37]], order 725760 Properties convex Alternate names
- Expanded 8-simplex
- Small exated enneazetton (soxeb) (Jonathan Bowers)[1]
Coordinates
The vertices of the heptellated 8-simplex can be most simply positioned in 8-space as permutations of (0,1,1,1,1,1,1,1,2). This construction is based on facets of the heptellated 9-orthoplex.
Root vectors
Its 72 vertices represent the root vectors of the simple Lie group A8.
Images
orthographic projections Ak Coxeter plane A8 A7 A6 A5 Graph 

Dihedral symmetry [[9]] [8] [[7]] [6] Ak Coxeter plane A4 A3 A2 Graph 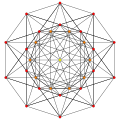
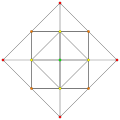
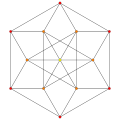
Dihedral symmetry [[5]] [4] [[3]] Omnitruncated 8-simplex
Omnitruncated 8-simplex Type uniform polyzetton Schläfli symbol t0,1,2,3,4,5,6,7{37} Coxeter-Dynkin diagrams 














7-faces 6-faces 5-faces 4-faces Cells Faces Edges 1451520 Vertices 362880 Vertex figure irr. 7-simplex Coxeter group A8, [[37]], order 725760 Properties convex The symmetry order of an omnitruncated 9-simplex is 725760. The symmetry of a family of a uniform polytopes is equal to the number of vertices of the omnitruncation, being 362880 (9 factorial) in the case of the omnitruncated 8-simplex; but when the CD symbol is palindromic, the symmetry order is doubled, 725760 here, because the element corresponding to any element of the underlying 8-simplex can be exchanged with one of those corresponding to an element of its dual.
Alternate names
- Heptihexipentisteriruncicantitruncated 8-simplex
- Great exated enneazetton (goxeb) (Jonathan Bowers)[2]
Coordinates
The Cartesian coordinates of the vertices of the omnitruncated 8-simplex can be most simply positioned in 9-space as permutations of (0,1,2,3,4,5,6,7,8). This construction is based on facets of the heptihexipentisteriruncicantitruncated 9-orthoplex, t0,1,2,3,4,5,6,7{37,4}
Images
orthographic projections Ak Coxeter plane A8 A7 A6 A5 Graph 



Dihedral symmetry [[9]] [8] [[7]] [6] Ak Coxeter plane A4 A3 A2 Graph 
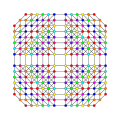
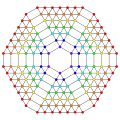
Dihedral symmetry [[5]] [4] [[3]] The omnitruncated 8-simplex is the permutohedron of order 9. The omnitruncated 8-simplex is a zonotope, the Minkowski sum of nine line segments parallel to the nine lines through the origin and the nine vertices of the 8-simplex.
Like all uniform omnitruncated n-simplices, the omnitruncated 8-simplex can tessellate space by itself, in this case 8-dimensional space with three facets around each ridge. It has Coxeter-Dynkin diagram of








 .
.Related polytopes
This polytope is one of 135 uniform 8-polytopes with A8 symmetry.

t0
t1
t2
t3
t01
t02
t12
t03
t13
t23
t04
t14
t24
t34
t05
t15
t25
t06
t16
t07
t012
t013
t023
t123
t014
t024
t124
t034
t134
t234
t0123
t0124
t0134
t0234
t1234
t1235
t1245
t1345
t2345
t01234
t12345
t01234567Notes
References
- H.S.M. Coxeter:
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, editied by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D.
- Richard Klitzing, 8D, uniform polytopes (polyzetta) x3o3o3o3o3o3o3x - soxeb, x3x3x3x3x3x3x3x - goxeb
External links
- Olshevsky, George, Cross polytope at Glossary for Hyperspace.
- Polytopes of Various Dimensions
- Multi-dimensional Glossary
Fundamental convex regular and uniform polytopes in dimensions 2–10 Family An BCn Dn E6 / E7 / E8 / F4 / G2 Hn Regular polygon Triangle Square Hexagon Pentagon Uniform polyhedron Tetrahedron Octahedron • Cube Demicube Dodecahedron • Icosahedron Uniform polychoron 5-cell 16-cell • Tesseract Demitesseract 24-cell 120-cell • 600-cell Uniform 5-polytope 5-simplex 5-orthoplex • 5-cube 5-demicube Uniform 6-polytope 6-simplex 6-orthoplex • 6-cube 6-demicube 122 • 221 Uniform 7-polytope 7-simplex 7-orthoplex • 7-cube 7-demicube 132 • 231 • 321 Uniform 8-polytope 8-simplex 8-orthoplex • 8-cube 8-demicube 142 • 241 • 421 Uniform 9-polytope 9-simplex 9-orthoplex • 9-cube 9-demicube Uniform 10-polytope 10-simplex 10-orthoplex • 10-cube 10-demicube n-polytopes n-simplex n-orthoplex • n-cube n-demicube 1k2 • 2k1 • k21 pentagonal polytope Topics: Polytope families • Regular polytope • List of regular polytopes Categories:- 8-polytopes
Wikimedia Foundation. 2010.
