Debye–Hückel theory

The Debye–Hückel theory was proposed by Peter Debye and Erich Hückel as a theoretical explanation for departures from ideality in solutions of electrolytes.^[1] It was based on an extremely simplified model of the electrolyte solution but nevertheless gave accurate predictions of mean activity coefficients for ions in dilute solution. The Debye-Hückel equation provides a starting point for modern treatments of non-ideality of electrolyte solutions.^[2]

Overview

In the chemistry of electrolyte solutions, an ideal solution is a solution whose colligative properties are proportional to the concentration of the solute. Real solutions show departures from this kind of ideality at all but the very lowest concentrations (see, for example, Raoult's law). In order to accommodate these effects in the thermodynamics of solutions, the concept of activity was introduced: the properties are then proportional to the activities of the ions. Activity, a, is proportional to concentration, c. The proportionality constant is known as an activity coefficient, γ.^[3]

a = γ c

In an ideal electrolyte solution the activity coefficients of all the ions are equal to one. Non-ideality arises principally (but not exclusively) because ions of opposite charge attract each other due to electrostatic forces, while ions of the same charge repel each other. In consequence ions are not randomly distributed throughout the solution, as they would be in an ideal solution.

Activity coefficients of single ions cannot be measured experimentally because an electrolyte solution must contain both positively charged ions and negatively charged ions. Instead, a mean activity coefficient, $\gamma_{\pm}$ is defined. For example, with the electrolyte NaCl

$\gamma_{\pm} = \left(\gamma_{Na^+}\gamma _{Cl^-}\right )^{1/2}$

In general, the mean activity coefficient of a fully dissociated electrolyte of formula A_nB_m is given by^[4]

$\gamma_{\pm} = \left({\gamma_A}^n{\gamma _B}^m\right )^{1/(n+m)}$

Activity coefficients are themselves functions of concentration as the amount of inter-ionic interaction increases as the concentration of the electrolyte increases. Debye and Hückel developed a theory with which single ion activity coefficients could be calculated. By calculating the mean activity coefficients from them the theory could be tested against experimental data. It was found to give excellent agreement for "dilute" solutions.

The model

An idealized representaltion of a solution of a 1:1 electrolyte

A description of Debye–Hückel theory includes a very detailed discussion of the assumptions and their limitations as well as the mathematical development and applications.^[5]

A snapshot of a 2-dimensional section of an idealized electrolyte solution is shown in the adjacent picture. The ions are shown as spheres with unit electrical charge. The solvent (pale blue) is shown as a uniform medium, without structure. On average, each ion is surrounded more closely by ions of opposite charge than by ions of like charge. These concepts were developed into a quantitative theory involving ions of charge z₁e⁺ and z₂e^-, where z can be any integer. The principal assumption is that departure from non-ideality is due to electrostatic interactions between ions, mediated by Coulomb's law: the force of interaction between two ions, separated by a distance, r in a medium of relative permittivity ε_r is given by^[6]

$\mbox{force} = \frac {z_1z_2e^2}{4\pi \epsilon _0 \epsilon _r r^2}$

It is also assumed that

• The dissolved electrolyte is completely dissociated; it is a strong electrolyte.
• Ions are spherical and are not polarized by the surrounding electric field. Solvation of ions is ignored except insofar as it determines the effective sizes of the ions.
• The solvent plays no role other than providing a medium of constant relative permittivity (dielectric constant).
• There is no Electrostriction.
• Individual ions surrounding a "central" ion can be represented by a statistically averaged cloud of continuous charge density, with a minimum distance of closest approach.

The last assumption means that each cation is surrounded by a spherically symmetric cloud of other ions. The cloud has a net negative charge. Similarly each anion is surrounded by a cloud with net positive charge.^[7]

Mathematical development

Main article: Debye-Hückel equation

The deviation from ideality is taken to be a function of the potential energy resulting from the electrostatic interactions between ions and their surrounding clouds. To calculate this energy two steps are needed.

The first step is to specify the electrostatic potential for ion j by means of Poisson's equation

$\nabla^2 \psi_j(r) = -\frac{1}{\epsilon _0 \epsilon _r}\rho _j(r)$

ψ(r) is the total potential at a distance, r, from the central ion and ρ(r) is the averaged charge density of the surrounding cloud at that distance. To apply this formula it is essential that the cloud has spherical symmetry, that is, the charge density is a function only of distance from the central ion as this allows the Poisson equation to be cast in terms of spherical coordinates with no angular dependence.^[8]

The second step is to calculate the charge density by means of a Maxwell-Boltzmann distribution.

$n'_i = n_i \mbox{exp}{\left(\frac{-z_ie\psi_j(r)}{kT}\right)}$

This distribution also depends on the potential ψ(r) and this introduces a serious difficulty in terms of the superposition principle. Nevertheless, the two equations can be combined to produce the Poisson-Boltzmann equation.^[9]

$\nabla^2\psi_j(r)=\frac{1}{\epsilon_0\epsilon_r} \sum_i \left\{n_i(z_ie)\mbox{exp} \left(\frac{-z_ie\psi_j(r)}{kT}\right)\right\}$

Solution of this equation is far from straightforward. It can be solved by successive approximations using modern electronic computers, but these were not available to Debye and Hückel. Instead they expanded the exponential as a truncated Taylor series. This results in the truncated Poisson-Boltzmann equation,^[10]

$\nabla^2\psi_j(r)=\frac{d^2}{dr^2}\psi_j(r)=\kappa^2\psi_j(r)$

which is a type of differential equation which has an analytical solution. This equation applies to 1:1, 2:2 and 3:3 electrolytes; for unsymmetrical electrolytes another term in ψ² must be included. Incidentally, the truncated expansion may also remove the difficulty with the superposition principle.

The solution for a symmetrical electrolyte, in terms of the mean activity coefficient is given as^[11]

Experimental log$\gamma_\pm$ values for KBr at 25°C (points)^[12] and Debye-Hückel limiting law (coloured line)

$\mbox{log}_{10}\gamma_\pm = -Az_i^2 \frac{\sqrt I}{1 +Ba_0\sqrt I}$

$A=\frac{e^2B}{2.303 \times 8\pi\epsilon_0\epsilon_r kT}$

$B=\left( \frac{2e^2 N}{\epsilon_0\epsilon_rkT} \right)^{1/2}$

I is the ionic strength and a₀ is a parameter which represent the distance of closest approach of ions. For aqueous solutions at 25 °C A = 0.051 mol^-1/2dm^3/2 and B = 3.29 mol^-1/2dm^3/2[13]

The most significant aspect of these algebraic manipulations is the prediction that the mean activity coefficient is a function of ionic strength. Of course the ionic strength of a 1:1 electrolyte is equal to its concentration, but that is not true for other types of electrolyte. Generally, activity coefficients are discussed in terms of ionic strength rather than the electrolyte concentration. For very low values of the ionic strength the value of the denominator in the expression above becomes nearly equal to one. In this situation the mean activity coefficient is proportional to the square root of the ionic strength. This is known as the Debye-Hückel limiting law.

Limitations and extensions

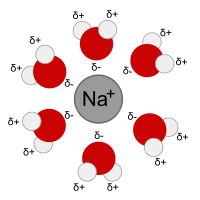The first solvation shell of a sodium ion dissolved in water. The oxygen atoms are arranged at the vertices of an octahedron with the sodium ion at its centre

The equation for log $\gamma_\pm$ gives satisfactory agreement with experimental measurements for low electrolyte concentrations, typically less than 10⁻³ mol dm⁻³. Deviations from the theory occur at higher concentrations and with electrolytes that produce ions of higher charges, particularly unsymmetrical electrolytes. Essentially these deviations occur because the model is hopelessly over-simplified, so there is little to be gained making small adjustments to the model.^[14] The individual assumptions can be challenged in turn.

• Complete dissociation. Ion association may take place, particularly with ions of higher charge. This was followed up in detail by Niels Bjerrum. The Bjerrum length is the separation at which the electrostatic interaction between two ions is comparable in magnitude to kT.
• Weak electrolytes. A weak electrolyte is one that is not fully dissociated. As such it has a dissociation constant. The dissociation constant can be used to calculate the extent of dissociation and hence, make the necessary correction needed to calculate activity coefficients.^[15]
• Ions are spherical and are not polarized. Many ions such as the nitrate ion, NO₃^-, are manifestly not spherical. Polyatomic ions are also polarizable.
• Role of the solvent. The solvent is not a structureless medium but is made up of molecules. The water molecules in aqueous solution are both dipolar and polarizable. Both cations and anions have a strong primary solvation shell and a weaker secondary solvation shell. Ion-solvent interactions are ignored in Debye–Hückel theory.

Moreover, we assume that the ionic radius is negligible, but at higher concentrations, the ionic radius becomes comparable to the radius of the ionic cloud! Most extensions to Debye–Hückel theory are empirical in nature. They usually allow the Debye–Hückel equation to be followed at low concentration and add further terms in some power of the ionic strength to fit experimental observations. The main extensions are the Davies equation, Pitzer equations and Specific ion interaction theory.

Conductivity

Forces affecting a charged ion or cloud moving in an electric field

The treatment given so far is for a system not subject to an external electric field. When conductivity is measured the system is subject to an oscillating external field due to the application of an AC voltage to electrodes immersed in the solution. Debye and Hückel modified their theory in 1926 and their theory was further modified by Lars Onsager in 1927. All the postulates of the original theory were retained. In addition it was assumed that the electric field causes the charge cloud to be distorted away from spherical symmetry.^[16] After taking this into account, together with the specific requirements of moving ions, such as viscosity and electrophoretic effects, Onsager was able to derive a theoretical expression to account for the empirical relation known as Kohlrausch's Law, for the molar conductivity, Λ_m.

$\Lambda_m =\Lambda_m^0-K\sqrt{c}$

$\Lambda_m^0$ is known as the limiting molar conductivity, K is an empirical constant and c is the electrolyte concentration Limiting here means "at the limit of the infinite dilution"). Onsager's expression is

$\Lambda_m =\Lambda_m^0-(A+B\Lambda_m^0 )\sqrt{c}$

where A and B are constants that depend only on known quantities such as temperature, the charges on the ions and the dielectric constant and viscosity of the solvent. This is known as the Debye-Hückel-Onsager equation. However, this equation only applies to very dilute solutions and has been largely superseded by other equations due to Fuoss and Onsager, 1932 and 1957 and later.^[17]

References

1. ^ P. Debye and E. Hückel (1923). "The theory of electrolytes. I. Lowering of freezing point and related phenomena" (PDF). Physikalische Zeitschrift 24: 185–206. http://electrochem.cwru.edu/estir/hist/hist-12-Debye-1.pdf. 
2. ^ Wright, M.R. (2007). An Introduction to Aqueous Electrolyte Solutions. Wiley. ISBN 978-0-470-84293-5. 
3. ^ Wright, section 1.10
4. ^ Wright, Section 8.23
5. ^ Wright, chapter 10.
6. ^ Wright, Section 10.3
7. ^ Wright, Section 10.3
8. ^ Wright, section 10.6.3
9. ^ Wright, section 10.6.8
10. ^ Wright, section 10.6.10
11. ^ Wright, section 10.6.15
12. ^ Data from Wright, Worked problem 8.17
13. ^ Wright, section 10.7
14. ^ Wright, section 10.9
15. ^ Davies, C.W. (1962). Ion Association. London: Butterworths. pp. 37–53. 
16. ^ Wright, section 12.3
17. ^ Wright, sections 12.10 to 12.17