- Conductivity (electrolytic)
-
The conductivity (or specific conductance) of an electrolyte solution is a measure of its ability to conduct electricity. The SI unit of conductivity is siemens per meter (S/m).
Conductivity measurements are used routinely in many industrial and environmental applications as a fast, inexpensive and reliable way of measuring the ionic content in a solution.[1] For example, the measurement of product conductivity is a typical way to monitor and continuously trend the performance of the water purification systems.
In many cases, conductivity is linked directly to the total dissolved solids (T.D.S.). High quality deionized water has a conductivity of about 5.5 μS/m, typical drinking water in the range of 5-50 mS/m, while sea water about 5 S/m[2] (i.e., sea water's conductivity is one million times higher than deionized water).
Conductivity is traditionally determined by measuring the AC resistance of the solution between two electrodes. Dilute solutions follow Kohlrausch's Laws of concentration dependence and additivity of ionic contributions. Onsager gave a theoretical explanation of Kohlrausch's law by extending Debye–Hückel theory.
Contents
Units
The SI unit of conductivity is S/m and, unless otherwise qualified, it refers to 25 °C (standard temperature). Often encountered in industry is the traditional unit of μS/cm. The numbers in μS/cm are lower than those in μS/m by a factor of 100 (i.e., a solution with a conductivity of 100 μS/m has a conductivity of 1 μS/cm). Occasionally a unit of "EC" (electrical conductivity) is found on scales of instruments: 1 EC = 1 μS/cm. Sometimes encountered is so-called mho (reciprocal of ohm): 1 mho/m = 1 S/m. Historically, mhos antedate Siemens by many decades; good vacuum-tube testers, for instance, gave transconductance readings in micromhos.
The commonly used standard cell has a width of 1 cm, and thus for very pure water in equilibrium with air would have a resistance of about 106 ohm, known as a megohm, occasionally misspelled as "megaohm".[3] Ultra-pure water could achieve 18 megohms or more. Thus in the past megohm-cm was used, sometimes abbreviated to "megohm".[4] Sometimes, a conductivity is given just in "microSiemens" (omitting the distance term in the unit). While this is an error, it can often be assumed to be equal to the traditional μS/cm. The typical conversion of conductivity to the total dissolved solids is done assuming that the solid is sodium chloride: 1 μS/cm is then an equivalent of about 0.6 mg of NaCl per kg of water.
Molar conductivity has the SI unit S m2 mol−1. Older publications use the unit Ω−1 cm2 mol−1.
Measurement
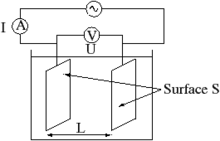
Main article: Electrical conductivity meterThe electrical conductivity of a solution of an electrolyte is measured by determining the resistance of the solution between two flat or cylindrical electrodes separated by a fixed distance.[5] An alternating voltage is used in order to avoid electrolysis. The resistance is measured by a conductivity meter. Typical frequencies used are in the range 1–3 kHz. The dependence on the frequency is usually small,[6] but may become appreciable at very high frequencies, an effect known as the Debye–Falkenhagen effect.
A wide variety of instrumentation is commercially available.[7] There are two types of cell, the classical type with flat or cylindrical electrodes and a second type based on induction.[8] Many commercial systems offer automatic temperature correction.
Definitions
Resistance, R, is proportional to the distance, l, between the electrodes and is inversely proportional to the cross-sectional area of the sample, A. Writing ρ (rho) for the specific resistance (or resistivity),
In practice the conductivity cell is calibrated by using solutions of known specific resistance, ρ*, so the quantities l and A need not be known precisely.[9] If the resistance of the calibration solution is R*, a cell-constant, C, is derived.
The specific conductance, κ (kappa) is the reciprocal of the specific resistance.
Conductivity is also temperature-dependent.
Theory
The conductivity of a solution containing one electrolyte depends on the concentration of the electrolyte. Therefore it is convenient to divide the conductivity by concentration. This quotient is termed molar conductivity, is denoted by Λm
Strong electrolytes
Strong electrolytes are believed to dissociate completely in solution. The conductivity of a solution of a strong electrolyte at low concentration follows Kohlrausch's Law
where
 is known as the limiting molar conductivity, K is an empirical constant and c is the electrolyte concentration. (Limiting here means "at the limit of the infinite dilution".)
is known as the limiting molar conductivity, K is an empirical constant and c is the electrolyte concentration. (Limiting here means "at the limit of the infinite dilution".)Moreover, Kohlrausch also found that the limiting conductivity of anions and cations are additive: the conductivity of a solution of a salt is equal to the sum of conductivity contributions from the cation and anion.
where:
- ν + and ν − are the number of moles of cations and anions, respectively, which are created from the dissociation of 1 mole of the dissolved electrolyte;
 and
and  are the limiting molar conductivities of the individual ions.
are the limiting molar conductivities of the individual ions.
The following table gives values for limiting molar conductivities for selected ions.
Limiting ion conductivity in water at 298 K Cations λ+0 /mS m2mol-1 anions λ-0 /mS m2mol-1 H+ 34.96 OH- 19.91 Li+ 3.869 Cl- 7.634 Na+ 45.011 Br- 7.84 K+ 7.350 I- 7.68 Mg2+ 10.612 SO42- 15.96 Ca2+ 11.900 NO3- 7.14 Ba2+ 12.728 CH3CO2- 4.09 A theoretical interpretation of these results was provided by the Debye-Hückel-Onsager equation.[10]
where A and B are constants that depend only on known quantities such as temperature, the charges on the ions and the dielectric constant and viscosity of the solvent. As the name suggests, this is an extension of the Debye–Hückel theory, due to Onsager. It is very successful for solutions at low concentration.
Weak electrolytes
A weak electrolyte is one that is not fully dissociated . Typical weak electrolytes are weak acids and weak bases. The concentration of ions in a solution of a weak electrolyte is less than the concentration of the electrolyte itself. For acids and bases the concentrations can be calculated when the value(s) of the acid dissociation constant(s) is(are) known.
For a monoprotic acid, HA, with a dissociation constant Ka, an explicit expression for the conductivity as a function of concentration, c, known as Ostwald's dilution law, can be obtained.
Higher concentrations
Both Kolrausch's law and the Debye-Hückel-Onsager equation break down as the concentration of the electrolyte increases above a certain value. The reason for this is that as concentration increases the average distance between cation and anion decreases, so that there is more inter-ionic interaction. Whether this constitutes ion-association is a moot point. However, It has often been assumed that cation and anion interact to form an ion-pair. Thus the electrolyte is treated as if it were like a weak acid and a constant, K, can be derived for the equilibrium
Davies describes the results of such calculations in great detail, but states that K should not necessarily be thought of as a true equilibrium constant, rather, the inclusion of an "ion-association" term is useful in extending the range of good agreement between theory and experimental conductivity data.[11] Various attempts have been made to extend Onsager's treament to more concentrated solutions.[12]
The existence of a so-called conductance minimum has proved to be a controversial subject as regards interpretation. Fuoss and Kraus suggested that it is caused by the formation of ion-triplets,[13] and this suggestion has received some support recently.[14][15]
Applications
Not with standing the difficulty of theoretical interpretation, conductivity measurements are used extensively in many industries.[16] For example, conductivity measurements are used to monitor quality in public water supplies, in hospitals, in boiler water and industries which depend on water quality such as brewing. This type of measurement is not ion-specific; it can sometimes be used to determine the amount of total dissolved solids (T.D.S.) if the composition of the solution and its conductivity behavior are known.[1]
Sometimes, conductivity measurements are linked with other methods to increase the sensitivity of detection of specific types of ions. For example, in the boiler water technology, the boiler blowdown is continuously monitored for "cation conductivity", which is the conductivity of the water after it has been passed through a cation exchange resin. This is a sensitive method of monitoring anion impurities in the boiler water in the presence of excess cations (those of the alkalizing agent usually used for water treatment). The sensitivity of this method relies on the high mobility of H+ in comparison with the mobility of other cations or anions.
Conductivity detectors are commonly used with ion chromatography.[17]
See also
- Debye–Falkenhagen effect
- Svante Arrhenius
- Alfred Werner - coordination chemistry
- Conductimetric titration - methods to determine the equivalence point
References
- ^ a b Gray, James R. (2004). "Conductivity Analyzers and Their Application". In Down, R.D; Lehr, J.H.. Environmental Instrumentation and Analysis Handbook. Wiley. pp. 491–510. ISBN 978-0-471-46354-2. http://books.google.com/books?id=6jhELyGJOm0C&pg=PA491. Retrieved 2009-05-10.
- ^ http://www.lenntech.com/water-conductivity.htm
- ^ Spelling unit names with prefixes "9 Rules and Style Conventions for Spelling Unit Names". NIST.gov. http://physics.nist.gov/Pubs/SP811/sec09.html#9.3 Spelling unit names with prefixes. Retrieved 2011-08-02.
- ^ An internet search of megohm and ultra-pure water will give examples of companies still doing this. The term "megohm water" is used by some.
- ^ Bockris, J. O'M.; Reddy, A.K.N; Gamboa-Aldeco , M. (1998). Modern Electrochemistry (2nd. ed.). Springer. ISBN 0306455552. http://books.google.com/?id=utDyTYpimkUC. Retrieved 2009-05-10.
- ^ Marija Bešter-Rogač and Dušan Habe, "Modern Advances in Electrical Conductivity Measurements of Solutions", Acta Chim. Slov. 2006, 53, 391–395 (pdf)
- ^ Boyes, W. (2002). Instrumentation Reference Book (3rd. ed.). Butterworth-Heinemann. ISBN 0750671238. http://books.google.com/?id=sarHIbCVOUAC. Retrieved 2009-05-10.
- ^ Gray, p 495
- ^ "ASTM D1125 - 95(2005) Standard Test Methods for Electrical Conductivity and Resistivity of Water". http://www.astm.org/Standards/D1125.htm. Retrieved 2009-05-12.
- ^ Wright, M.R. (2007). An Introduction to Aqueous Electrolyte Solutions. Wiley. ISBN 978-0-470-84293-5.
- ^ Davies, C.W. (1962). Ion Association. London: Butterworths.
- ^ Miyoshi, K. (1973). "Comparison of the Conductance Equations of Fuoss - Onsager, Fuoss-Hsia and Pitts with the Data of Bis(2, 9-dimethyl-1, 10-phenanthroline)Cu(I) Perchlorate". Bull. Chem. Soc. Japan 46 (2): 426–430. doi:10.1246/bcsj.46.426.
- ^ Fuoss, R.M.; Kraus, C.A. (1935). "Properties of Electrolytic Solutions. XV. Thermodynamic Properties of Very Weak Electrolytes". J. Amer. Chem. Soc. 57: 1–4. doi:10.1021/ja01304a001.
- ^ Weingärtner, H.; Weiss, V.C.; Schröer, W. (2000). "Ion association and electrical conductance minimum in Debye–Hückel-based theories of the hard sphere ionic fluid". J. Chem. Phys. 113 (2): 762-. Bibcode 2000JChPh.113..762W. doi:10.1063/1.481822.
- ^ Schröer, W.; Weingärtner, H. (2004). "Structure and criticality of ionic fluids". Pure Appl. Chem. 76 (1): 19–27. doi:10.1351/pac200476010019. pdf
- ^ "Electrolytic conductivity measurement, Theory and practice". Aquarius Technologies Pty Ltd.. http://www.aquariustech.com.au/pdfs/tech-bulletins/Electrol_Condct_Thery.pdf.
- ^ "Detectors for ion-exchange chromatography". http://www.chromatography-online.org/ion-chromatography/Detectors-for-Ion-Exchange-Chromatography.html. Retrieved 2009-05-17.
External links
- Cole-Parmer Technical Library Conductivity
- Conductivity measurement PowerPoint presentation
Categories:
Wikimedia Foundation. 2010.