- Prim's algorithm
-
Graph and tree
search algorithmsAlpha-beta pruning
A*
B*
Beam
Bellman–Ford algorithm
Best-first
Bidirectional
Breadth-first
D*
Depth-first
Depth-limited
Dijkstra's algorithm
Floyd–Warshall algorithm
Hill climbing
Iterative deepening depth-first Johnson's algorithm
Lexicographic breadth-first
Uniform-cost
moreRelated topics Dynamic programming
Search gamesIn computer science, Prim's algorithm is a greedy algorithm that finds a minimum spanning tree for a connected weighted undirected graph. This means it finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized. The algorithm was developed in 1930 by Czech mathematician Vojtěch Jarník and later independently by computer scientist Robert C. Prim in 1957 and rediscovered by Edsger Dijkstra in 1959. Therefore it is also sometimes called the DJP algorithm, the Jarník algorithm, or the Prim–Jarník algorithm.
Other algorithms for this problem include Kruskal's algorithm and Borůvka's algorithm.
Contents
Description
Prim's algorithm has many applications, such as in the generation of this maze, which applies Prim's algorithm to a randomly weighted grid graph.
The only spanning tree of the empty graph (with an empty vertex set) is again the empty graph. The following description assumes that this special case is handled separately.
The algorithm continuously increases the size of a tree, one edge at a time, starting with a tree consisting of a single vertex, until it spans all vertices.
- Input: A non-empty connected weighted graph with vertices V and edges E (the weights can be negative).
- Initialize: Vnew = {x}, where x is an arbitrary node (starting point) from V, Enew = {}
- Repeat until Vnew = V:
- Choose an edge (u, v) with minimal weight such that u is in Vnew and v is not (if there are multiple edges with the same weight, any of them may be picked)
- Add v to Vnew, and (u, v) to Enew
- Output: Vnew and Enew describe a minimal spanning tree
Time complexity
Minimum edge weight data structure Time complexity (total) adjacency matrix, searching O(V2)[1] binary heap and adjacency list O((V + E) log V) = O(E log V) Fibonacci heap and adjacency list O(E + V log V) A simple implementation using an adjacency matrix graph representation and searching an array of weights to find the minimum weight edge to add requires O(V2) running time. Using a simple binary heap data structure and an adjacency list representation, Prim's algorithm can be shown to run in time O(E log V) where E is the number of edges and V is the number of vertices. Using a more sophisticated Fibonacci heap, this can be brought down to O(E + V log V), which is asymptotically faster when the graph is dense enough that E is Ω(V).
Example run
Image Description 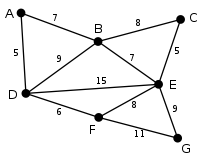
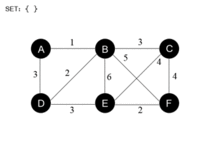
This is our original weighted graph. The numbers near the edges indicate their weight. 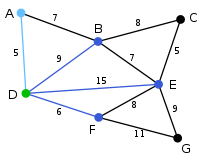
Vertex D has been arbitrarily chosen as a starting point. Vertices A, B, E and F are connected to D through a single edge. A is the vertex nearest to D and will be chosen as the second vertex along with the edge AD. 
The next vertex chosen is the vertex nearest to either D or A. B is 9 away from D and 7 away from A, E is 15, and F is 6. F is the smallest distance away, so we highlight the vertex F and the arc DF. 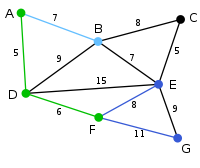
The algorithm carries on as above. Vertex B, which is 7 away from A, is highlighted. 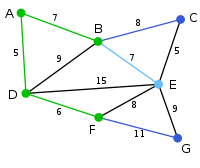
In this case, we can choose between C, E, and G. C is 8 away from B, E is 7 away from B, and G is 11 away from F. E is nearest, so we highlight the vertex E and the arc BE. 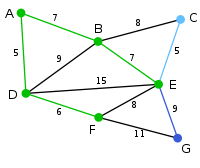
Here, the only vertices available are C and G. C is 5 away from E, and G is 9 away from E. C is chosen, so it is highlighted along with the arc EC. 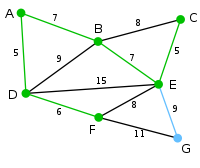
Vertex G is the only remaining vertex. It is 11 away from F, and 9 away from E. E is nearer, so we highlight it and the arc EG. 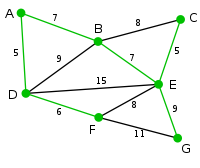
Now all the vertices have been selected and the minimum spanning tree is shown in green. In this case, it has weight 39. U Edge(u,v) V \ U {} {A,B,C,D,E,F,G} {D} (D,A) = 5 V
(D,B) = 9
(D,E) = 15
(D,F) = 6{A,B,C,E,F,G} {A,D} (D,B) = 9
(D,E) = 15
(D,F) = 6 V
(A,B) = 7{B,C,E,F,G} {A,D,F} (D,B) = 9
(D,E) = 15
(A,B) = 7 V
(F,E) = 8
(F,G) = 11{B,C,E,G} {A,B,D,F} (B,C) = 8
(B,E) = 7 V
(D,B) = 9 cycle
(D,E) = 15
(F,E) = 8
(F,G) = 11{C,E,G} {A,B,D,E,F} (B,C) = 8
(D,B) = 9 cycle
(D,E) = 15 cycle
(E,C) = 5 V
(E,G) = 9
(F,E) = 8 cycle
(F,G) = 11{C,G} {A,B,C,D,E,F} (B,C) = 8 cycle
(D,B) = 9 cycle
(D,E) = 15 cycle
(E,G) = 9 V
(F,E) = 8 cycle
(F,G) = 11{G} {A,B,C,D,E,F,G} (B,C) = 8 cycle
(D,B) = 9 cycle
(D,E) = 15 cycle
(F,E) = 8 cycle
(F,G) = 11 cycle{} Proof of correctness
Let P be a connected, weighted graph. At every iteration of Prim's algorithm, an edge must be found that connects a vertex in a subgraph to a vertex outside the subgraph. Since P is connected, there will always be a path to every vertex. The output Y of Prim's algorithm is a tree, because the edge and vertex added to Y are connected. Let Y1 be a minimum spanning tree of P. If Y1=Y then Y is a minimum spanning tree. Otherwise, let e be the first edge added during the construction of Y that is not in Y1, and V be the set of vertices connected by the edges added before e. Then one endpoint of e is in V and the other is not. Since Y1 is a spanning tree of P, there is a path in Y1 joining the two endpoints. As one travels along the path, one must encounter an edge f joining a vertex in V to one that is not in V. Now, at the iteration when e was added to Y, f could also have been added and it would be added instead of e if its weight was less than e. Since f was not added, we conclude that
Let Y2 be the graph obtained by removing f from and adding e to Y1. It is easy to show that Y2 is connected, has the same number of edges as Y1, and the total weights of its edges is not larger than that of Y1, therefore it is also a minimum spanning tree of P and it contains e and all the edges added before it during the construction of V. Repeat the steps above and we will eventually obtain a minimum spanning tree of P that is identical to Y. This shows Y is a minimum spanning tree.
References
- ^ Ashar, Jayen. "Prim’s Algorithm in V^2". https://cgi.cse.unsw.edu.au/~jayen/blog/prims-algorithm-in-v2/. Retrieved 11 October 2011.
- V. Jarník: O jistém problému minimálním [About a certain minimal problem], Práce Moravské Přírodovědecké Společnosti, 6, 1930, pp. 57–63. (in Czech)
- R. C. Prim: Shortest connection networks and some generalizations. In: Bell System Technical Journal, 36 (1957), pp. 1389–1401
- D. Cherition and R. E. Tarjan: Finding minimum spanning trees. In: SIAM Journal on Computing, 5 (Dec. 1976), pp. 724–741
- Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Third Edition. MIT Press, 2009. ISBN 0-262-03384-4. Section 23.2: The algorithms of Kruskal and Prim, pp. 631–638.
External links
Categories:- Graph algorithms
- Spanning tree
Wikimedia Foundation. 2010.