Iterative deepening depth-first search

Graph and tree search algorithms
Alpha-beta pruning A* B* Beam Bellman–Ford algorithm Best-first Bidirectional Breadth-first D* Depth-first Depth-limited Dijkstra's algorithm Floyd–Warshall algorithm Hill climbing Iterative deepening depth-first Johnson's algorithm Lexicographic breadth-first Uniform-cost more
Related topics
Dynamic programming Search games
v · d · e

Iterative deepening depth-first search (IDDFS) is a state space search strategy in which a depth-limited search is run repeatedly, increasing the depth limit with each iteration until it reaches d, the depth of the shallowest goal state. On each iteration, IDDFS visits the nodes in the search tree in the same order as depth-first search, but the cumulative order in which nodes are first visited, assuming no pruning, is effectively breadth-first.

Properties

IDDFS combines depth-first search's space-efficiency and breadth-first search's completeness (when the branching factor is finite). It is optimal when the path cost is a non-decreasing function of the depth of the node.

The space complexity of IDDFS is O(bd), where b is the branching factor and d is the depth of shallowest goal. Since iterative deepening visits states multiple times, it may seem wasteful, but it turns out to be not so costly, since in a tree most of the nodes are in the bottom level, so it does not matter much if the upper levels are visited multiple times.^[1]

The main advantage of IDDFS in game tree searching is that the earlier searches tend to improve the commonly used heuristics, such as the killer heuristic and alpha-beta pruning, so that a more accurate estimate of the score of various nodes at the final depth search can occur, and the search completes more quickly since it is done in a better order. For example, alpha-beta pruning is most efficient if it searches the best moves first.^[1]

A second advantage is the responsiveness of the algorithm. Because early iterations use small values for d, they execute extremely quickly. This allows the algorithm to supply early indications of the result almost immediately, followed by refinements as d increases. When used in an interactive setting, such as in a chess-playing program, this facility allows the program to play at any time with the current best move found in the search it has completed so far. This is not possible with a traditional depth-first search.

The time complexity of IDDFS in well-balanced trees works out to be the same as Depth-first search: O(b^d).

In an iterative deepening search, the nodes on the bottom level are expanded once, those on the next to bottom level are expanded twice, and so on, up to the root of the search tree, which is expanded d + 1 times.^[1] So the total number of expansions in an iterative deepening search is

$(d + 1)1 + (d)b + (d-1)b^{2} + \cdots + 3b^{d-2} + 2b^{d-1} + b^{d}$

$\sum_{i=0}^d (d+1-i)b^i$

For b = 10 and d = 5 the number is

6 + 50 + 400 + 3,000 + 20,000 + 100,000 = 123,456

All together, an iterative deepening search from depth 1 to depth d expands only about 11% more nodes than a single breadth-first or depth-limited search to depth d, when b = 10. The higher the branching factor, the lower the overhead of repeatedly expanded states, but even when the branching factor is 2, iterative deepening search only takes about twice as long as a complete breadth-first search. This means that the time complexity of iterative deepening is still O(b^d), and the space complexity is O(bd). In general, iterative deepening is the preferred search method when there is a large search space and the depth of the solution is not known.^[1]

Example

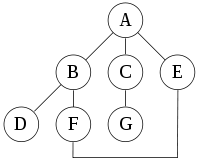
For the following graph:

a depth-first search starting at A, assuming that the left edges in the shown graph are chosen before right edges, and assuming the search remembers previously-visited nodes and will not repeat them (since this is a small graph), will visit the nodes in the following order: A, B, D, F, E, C, G. The edges traversed in this search form a Trémaux tree, a structure with important applications in graph theory.

Performing the same search without remembering previously visited nodes results in visiting nodes in the order A, B, D, F, E, A, B, D, F, E, etc. forever, caught in the A, B, D, F, E cycle and never reaching C or G.

Iterative deepening prevents this loop and will reach the following nodes on the following depths, assuming it proceeds left-to-right as above:

• 0: A
• 1: A (repeated), B, C, E

(Note that iterative deepening has now seen C, when a conventional depth-first search did not.)

• 2: A, B, D, F, C, G, E, F

(Note that it still sees C, but that it came later. Also note that it sees E via a different path, and loops back to F twice.)

• 3: A, B, D, F, E, C, G, E, F, B

For this graph, as more depth is added, the two cycles "ABFE" and "AEFB" will simply get longer before the algorithm gives up and tries another branch.

-

Pseudocode

IDDFS(root, goal)
{
  depth = 0
  while(no solution)
  {
    solution = DLS(root, goal, depth)
    depth = depth + 1
  }
  return solution
}

DLS(node, goal, depth) 
{
  if ( depth >= 0 ) 
   {
    if ( node == goal )
      return node

    for each child in expand(node)
      DLS(child, goal, depth-1)
  }
}

Related algorithms

Similar to iterative deepening is a search strategy called iterative lengthening search that works with increasing path-cost limits instead of depth-limits. It expands nodes in the order of increasing path cost; therefore the first goal it encounters is the one with the cheapest path cost. But iterative lengthening incurs substantial overhead that make it less useful than iterative deepening.

Notes

1. ^ ^{a b c d} Russell, Stuart J.; Norvig, Peter (2003), Artificial Intelligence: A Modern Approach (2nd ed.), Upper Saddle River, New Jersey: Prentice Hall, ISBN 0-13-790395-2, http://aima.cs.berkeley.edu/