Tree traversal

Graph and tree search algorithms
Alpha-beta pruning A* B* Beam Bellman–Ford algorithm Best-first Bidirectional Breadth-first D* Depth-first Depth-limited Dijkstra's algorithm Floyd–Warshall algorithm Hill climbing Iterative deepening depth-first Johnson's algorithm Lexicographic breadth-first Uniform-cost more
Related topics
Dynamic programming Search games
v · d · e

In computer science, tree-traversal refers to the process of visiting (examining and/or updating) each node in a tree data structure, exactly once, in a systematic way. Such traversals are classified by the order in which the nodes are visited. The following algorithms are described for a binary tree, but they may be generalized to other trees as well.

Traversal

Compared to linear data structures like linked lists and one dimensional arrays, which have a canonical method of traversal, tree structures can be traversed in many different ways. Starting at the root of a binary tree, there are three main steps that can be performed and the order in which they are performed defines the traversal type. These steps (in no particular order) are: performing an action on the current node (referred to as "visiting" the node), traversing to the left child node, and traversing to the right child node. Thus the process is most easily described through recursion.

The names given for particular style of traversal came from the position of root element with regard to the left and right nodes. Imagine that the left and right nodes are constant in space, then the root node could be placed to the left of the left node (pre-order), between the left and right node (in-order), or to the right of the right node (post-order).

For the purpose of illustration, it is assumed that left nodes always have priority over right nodes. This ordering can be reversed as long as the same ordering is assumed for all traversal methods.

Depth-first Traversal

See also: Depth-first search

Binary Tree

To traverse a non-empty binary tree in preorder, perform the following operations recursively at each node, starting with the root node:

1. Visit the root.
2. Traverse the left subtree.
3. Traverse the right subtree.

To traverse a non-empty binary tree in inorder (symmetric), perform the following operations recursively at each node:

1. Traverse the left subtree.
2. Visit the root.
3. Traverse the right subtree.

To traverse a non-empty binary tree in postorder, perform the following operations recursively at each node:

1. Traverse the left subtree.
2. Traverse the right subtree.
3. Visit the root.

Generic Tree

To traverse a non-empty tree in depth-first order, perform the following operations recursively at each node:

1. Perform pre-order operation
2. for i=1 to n-1 do
   1. Visit child[i], if present
   2. Perform in-order operation
3. Visit child[n], if present
4. Perform post-order operation

where n is the number of child nodes. Depending on the problem at hand, the pre-order, in-order or post-order operations may be void, or you may only want to visit a specific child node, so these operations should be considered optional. Also, in practice more than one of pre-order, in-order and post-order operations may be required. For example, when inserting into a ternary tree, a pre-order operation is performed by comparing items. A post-order operation may be needed afterwards to rebalance the tree.

Breadth-first Traversal

See also: Breadth-first search

Trees can also be traversed in level-order, where we visit every node on a level before going to a lower level. This is also called Breadth-first traversal.

Example

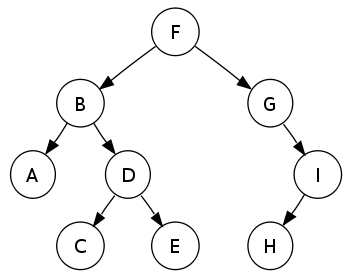
Binary search tree:

Depth-first

• Preorder traversal sequence: F, B, A, D, C, E, G, I, H (root, left, right)
• Inorder traversal sequence: A, B, C, D, E, F, G, H, I (left, root, right); note how this produces a sorted sequence
• Postorder traversal sequence: A, C, E, D, B, H, I, G, F (left, right, root)

Breadth-first

• Level-order traversal sequence: F, B, G, A, D, I, C, E, H

pre-order	in-order	post-order	level-order
push F pop F push G B pop B push D A pop A pop D push E C pop C pop E pop G push I pop I push H pop H	push F B A pop A pop B push D C pop C pop D push E pop E pop F push G pop G push I H pop H pop I	push F B A pop A push D C pop C push E pop E pop D pop B push G I H pop H pop I pop G pop F	enqueue F dequeue F enqueue B G dequeue B enqueue A D dequeue G enqueue I dequeue A dequeue D enqueue C E dequeue I enqueue H dequeue C dequeue E dequeue H

Sample implementations

preorder(node)
  if node = null then return
  print node.value
  preorder(node.left) 
  preorder(node.right)

inorder(node)
  if node = null then return
  inorder(node.left)
  print node.value
  inorder(node.right)

postorder(node)
  if node = null then return
  postorder(node.left)
  postorder(node.right)
  print node.value

All sample implementations will require call stack space proportional to the height of the tree. In a poorly balanced tree, this can be quite considerable.

We can remove the stack requirement by maintaining parent pointers in each node, or by threading the tree. In the case of using threads, this will allow for greatly improved inorder traversal, although retrieving the parent node required for preorder and postorder traversal will be slower than a simple stack based algorithm.

To traverse a threaded tree inorder, we could do something like this:

inorder(node)
  while hasleftchild(node) do
    node = node.left
  do
    visit(node)
    if (hasrightchild(node)) then
      node = node.right
      while hasleftchild(node) do
        node = node.left
    else
      while node.parent ≠ null and node == node.parent.right do
        node = node.parent
      node = node.parent
  while node ≠ null

Note that a threaded binary tree will provide a means of determining whether a pointer is a child, or a thread. See threaded binary trees for more information.

Queue-based level order traversal

Also, listed below is pseudocode for a simple queue based level order traversal, and will require space proportional to the maximum number of nodes at a given depth. This can be as much as the total number of nodes / 2. A more space-efficient approach for this type of traversal can be implemented using an iterative deepening depth-first search.

levelorder(root) 
  q = empty queue
  q.enqueue(root)
  while not q.empty do
    node := q.dequeue()
    visit(node)
    if node.left ≠ null
      q.enqueue(node.left)
    if node.right ≠ null
      q.enqueue(node.right)

Uses

Inorder traversal

It is particularly common to use an inorder traversal on a binary search tree because this will return values from the underlying set in order, according to the comparator that set up the binary search tree (hence the name).

To see why this is the case, note that if n is a node in a binary search tree, then everything in n 's left subtree is less than n, and everything in n 's right subtree is greater than or equal to n. Thus, if we visit the left subtree in order, using a recursive call, and then visit n, and then visit the right subtree in order, we have visited the entire subtree rooted at n in order. We can assume the recursive calls correctly visit the subtrees in order using the mathematical principle of structural induction. Traversing in reverse inorder similarly gives the values in decreasing order.

Preorder traversal

Traversing a tree in preorder while inserting the values into a new tree is common way of making a complete copy of a binary search tree.

One can also use preorder traversals to get a prefix expression (Polish notation) from expression trees: traverse the expression tree preorderly. To calculate the value of such an expression: scan from right to left, placing the elements in a stack. Each time we find an operator, we replace the two top symbols of the stack with the result of applying the operator to those elements. For instance, the expression ∗ + 2 3 4, which in infix notation is (2 + 3) ∗ 4, would be evaluated like this:

Using prefix traversal to evaluate an expression tree

Expression (remaining)	Stack
∗ + 2 3 4	<empty>
∗ + 2 3	4
∗ + 2	3 4
∗ +	2 3 4
∗	5 4
Answer	20

Functional traversal

We could perform the same traversals in a functional language like Haskell using code similar to this:

 data Tree a = Nil | Node (Tree a) a (Tree a)
 
 preorder Nil = []
 preorder (Node left x right) = [x] ++ (preorder left) ++ (preorder right)
 
 postorder Nil = []
 postorder (Node left x right) = (postorder left) ++ (postorder right) ++ [x]
 
 inorder Nil = []
 inorder (Node left x right) = (inorder left) ++ [x] ++ (inorder right)
 
 levelorder t = step [t]
     where
           step [] = []
           step ts = concatMap elements ts ++ step (concatMap subtrees ts)
           elements Nil = []
           elements (Node left x right) = [x]
           subtrees Nil = []
           subtrees (Node left x right) = [left, right]

Iterative Traversal

All the above recursive algorithms require stack space proportional to the depth of the tree. Recursive traversal may be converted into an iterative one using various well-known methods.

A sample is shown here for postorder traversal using a visited flag:

iterativePostorder(rootNode)
  nodeStack.push(rootNode)
  while (! nodeStack.empty())
    currNode = nodeStack.peek()
    if ((currNode.left != null) and (currNode.left.visited == false))
      nodeStack.push(currNode.left)
    else 
      if ((currNode.right != null) and (currNode.right.visited == false))
        nodeStack.push(currNode.right)
      else
        print currNode.value
        currNode.visited := true
        nodeStack.pop()

In this case each node is required to keep an additional "visited" flag, other than usual information (value, left-child-reference, right-child-reference).

Another sample is shown here for postorder traversal without requiring any additional bookkeeping flags (C++):

void iterativePostOrder(Node* root) {
        if (!root) {
                return;
        }
        stack<Node*> nodeStack;
 
        Node* cur = root;
        while (true) {
                if (cur) {
                        if (cur->right) {
                                nodeStack.push(cur->right);
                        }
                        nodeStack.push(cur);
                        cur = cur->left;
                        continue;
                }
 
                if (nodeStack.empty()) {
                        return;
                }
 
                cur = nodeStack.top(); 
                nodeStack.pop();
 
                if (cur->right && !nodeStack.empty() && cur->right == nodeStack.top()) {
                        nodeStack.pop();
                        nodeStack.push(cur);
                        cur = cur->right;
                } else {
                        std::cout << cur->val << " ";
                        cur = NULL;
                }
        }
}

Another example is preorder traversal without using a visited flag (Java):

public void iterativePreorder(Node root) {
        Stack nodes = new Stack();
        nodes.push(root);
 
        Node currentNode;
 
        while (!nodes.isEmpty()) {
                currentNode = nodes.pop();
                Node right = currentNode.right();
                if (right != null) {
                        nodes.push(right);
                }
                Node left = currentNode.left();
                if (left != null) {
                        nodes.push(left);      
                }
                System.out.println("Node data: "+currentNode.data);
        }
}

If each node holds reference to the parent node, then iterative traversal is possible without a stack or "visited" flag.

Here is another example of iterative inorder traversal in (C++):

void iterativeInorder(Node* root) {
        stack<Node*> nodeStack;
        Node *curr = root;
        while (true) {
                if (curr) {
                        nodeStack.push(curr);
                        curr = curr->left;
                        continue;
                }   
                if (!nodeStack.size()) {
                        return;
                }   
                curr = nodeStack.top();
                nodeStack.pop();
                std::cout << "Node data: " << curr->data << std::endl;
                curr = curr->right;
        }
}

Iterative inorder traversal in (Java):

public void traverseTreeInOrder(Node node) {
    //incoming node is root
    Stack<Node> nodes = new Stack<Node>();
    while (!nodes.isEmpty() || null != node) {
        if (null != node) {
            nodes.push(node);
            node = node.left;
        } else {
            node = nodes.pop();
            System.out.println("Node value: " + node.value);
            node = node.right;
        }
    }                     
}

See also

• Polish notation
• Depth-first search
• Breadth-first search
• Threaded binary tree - linear traversal of binary tree
• Nested set model

References

• Dale, Nell. Lilly, Susan D. "Pascal Plus Data Structures". D. C. Heath and Company. Lexington, MA. 1995. Fourth Edition.
• Drozdek, Adam. "Data Structures and Algorithms in C++". Brook/Cole. Pacific Grove, CA. 2001. Second edition.
• http://www.math.northwestern.edu/~mlerma/courses/cs310-05s/notes/dm-treetran

External links

• Animation Applet of Binary Tree Traversal
• The Adjacency List Model for Processing Trees with SQL
• Storing Hierarchical Data in a Database with traversal examples in PHP
• Managing Hierarchical Data in MySQL
• Working with Graphs in MySQL
• Non-recursive traversal of DOM trees in JavaScript
• Sample code for recursive and iterative tree traversal implemented in C.
• Sample code for recursive tree traversal in C#.
• See tree traversal implemented in various programming language on Rosetta Code
• Tree traversal without recursion